Median (stochastics)

This article covers the median of a probability distribution or distribution of a random variable.

• For the median of a sample, see median .
• For further meanings, see Median (disambiguation) .

In stochastics, the median , also called the central value, is a measure of the position of probability distributions and distributions of random variables . Thus, like the expected value and the mode, it is an indicator of where the "middle" of a probability distribution is. The median is clearly the number for which

• the probability of receiving a value less than or equal to the median and
• the probability of receiving a value greater than or equal to the median

is equal to. There are several formalizations of this intuitive notion that differ in terms of the existence and uniqueness of the median.

In the descriptive statistics which is median for sampling defined. The two terms differ in that one is an indicator of a sample (similar to the arithmetic mean ), the other is an indicator of a probability distribution (similar to the expected value ). The two are different per se, but can be linked via the empirical distribution .

First definition

For probability distributions

A probability distribution is given , i.e. the real numbers , provided with Borel's σ-algebra . ${\displaystyle P}$ ${\displaystyle (\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))}$

Then a real number is called a median (of ) if: ${\displaystyle m}$ ${\displaystyle P}$

${\displaystyle P((-\infty ,m])\geq {\tfrac {1}{2}}}$and . ${\displaystyle P([m,+\infty ))\geq {\tfrac {1}{2}}}$

For random variables

A real random variable is given . ${\displaystyle X}$

Then a real number is called a median (of ) if: ${\displaystyle m}$ ${\displaystyle X}$

${\displaystyle P(X\leq m)\geq {\tfrac {1}{2}}}$and . ${\displaystyle P(m\leq X)\geq {\tfrac {1}{2}}}$

The median of the random variable is therefore exactly the median of its distribution . ${\displaystyle X}$ ${\displaystyle P_{X}}$

Definition via distribution functions

The median can also be defined using distribution functions. If the distribution function is from or from , then a median (from or from ) is called if ${\displaystyle F}$ ${\displaystyle P}$ ${\displaystyle X}$ ${\displaystyle m}$ ${\displaystyle P}$ ${\displaystyle X}$

${\displaystyle F(m)\geq {\tfrac {1}{2}}\quad }$and . ${\displaystyle \quad \lim _{t\uparrow m}F(t)\leq {\tfrac {1}{2}}}$

Here is the limit value on the left . ${\displaystyle \lim _{t\uparrow m}F(t)}$

Determination and examples

With a continuous distribution function

If the distribution function is continuous , then is a median if and only if there is a solution of the equation ${\displaystyle F}$ ${\displaystyle m}$ ${\displaystyle m}$

${\displaystyle F(m)={\tfrac {1}{2}}}$

is.

This is based on the fact that the left-hand limit value then coincides with the function value.

Examples

Median of the exponential distribution

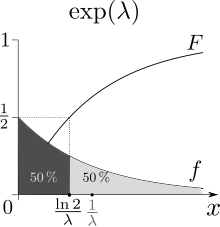
If one looks at the exponential distribution as an example , it has the distribution function

${\displaystyle F(x)={\begin{cases}1-\mathrm {e} ^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}}$

for a parameter . Equating with leads to the equation ${\displaystyle \lambda >0}$ ${\displaystyle {\tfrac {1}{2}}}$

${\displaystyle {\tfrac {1}{2}}=\mathrm {e} ^{-\lambda m}}$,

which is the solution

${\displaystyle m={\frac {\ln 2}{\lambda }}}$

owns. In this case the median is clear.

Plot of the Cantor function (10 iterations)

But the median can be ambiguous even with a constant distribution function. If, for example, one looks at the Cantor distribution , the distribution function of which is shown on the right, this assumes the value over the entire interval due to its construction . Each point in this interval is therefore a median. In the case of a constant distribution function, the median is unambiguous, for example, when the distribution function increases strictly monotonically. More specifically, the uniqueness already applies when the distribution function in the one environment in which it assumes the value is growing strictly monotonically. ${\displaystyle [{\tfrac {1}{3}},{\tfrac {2}{3}})}$ ${\displaystyle {\tfrac {1}{2}}}$ ${\displaystyle {\tfrac {1}{2}}}$

With probability densities

If the random variable or the probability distribution has a probability density function (it is therefore an absolutely continuous distribution ), the median is the solution of the equation ${\displaystyle f}$ ${\displaystyle m}$

${\displaystyle \int _{-\infty }^{m}f(x)\mathrm {d} x={\tfrac {1}{2}}}$.

This follows directly from the fact that absolutely continuous distributions always have a continuous distribution function, this can be determined via the integral and the statement in the section above.

Several medians occur here, for example, if the probability density function is constantly zero over an interval.

example

Looking at the probability function

${\displaystyle f(x)={\begin{cases}0&{\text{ falls }}\quad x\leq -1{\text{ oder }}x>1\\{\tfrac {1}{2}}&{\text{ falls }}\quad x\in (-1,-{\tfrac {1}{2}}]{\text{ oder }}x\in ({\tfrac {1}{2}},1]\\0&{\text{ falls }}\quad x\in (-{\tfrac {1}{2}},{\tfrac {1}{2}}]\\\end{cases}}}$,

so this is constant zero in the interval . Using the elementary integration rules, it then follows that every value is in a median. Solving the integral equation usually corresponds to the determination of the corresponding distribution function and can therefore be viewed as a special case of the procedure in the section above. ${\displaystyle (-{\tfrac {1}{2}},{\tfrac {1}{2}})}$ ${\displaystyle [-{\tfrac {1}{2}},{\tfrac {1}{2}})}$

Clear definition

A probability distribution or a real random variable is given . Let be the distribution function of or . Then is called ${\displaystyle P}$ ${\displaystyle X}$ ${\displaystyle F}$ ${\displaystyle P}$ ${\displaystyle X}$

${\displaystyle m=\inf\{x\in \mathbb {R} \mid F(x)\geq {\tfrac {1}{2}}\}}$

the median of or . This corresponds to the following definition: Is the quantile function to , the median is defined as ${\displaystyle P}$ ${\displaystyle X}$ ${\displaystyle Q}$ ${\displaystyle F}$

${\displaystyle m:=Q({\tfrac {1}{2}})}$.

Due to the legal continuity of the distribution function, the infimum can also be replaced by a minimum in the upper of the two definitions .

properties

The median is a quantile , more precisely the 50% quantile.

If the distribution is symmetrical , that is, zero is a median. More generally, the axis of symmetry is a median for any symmetrical distribution. ${\displaystyle P_{-X}=P_{X}}$

Every median minimizes the absolute deviation, i.e. if it is a random variable with , this always applies ${\displaystyle m}$ ${\displaystyle X}$ ${\displaystyle \operatorname {E} (|X|)<\infty }$

${\displaystyle \operatorname {E} (|X-a|)\geq \operatorname {E} (|X-m|)}$ for all ${\displaystyle a\in \mathbb {R} }$

and equality holds if and only if is also a median. ${\displaystyle a}$

Relation to the median of the descriptive statistics

The median in descriptive statistics (as a key figure of a sample) can be related to the median of a probability distribution via the empirical distribution : If a sample is given and the empirical distribution is then a median (in the sense of probability theory) of a Median (in the sense of descriptive statistics) of . Due to the different definitions, however, there may be slight deviations. ${\displaystyle x=(x_{1},x_{2},\dots ,x_{n})}$ ${\displaystyle E_{x}}$ ${\displaystyle x}$ ${\displaystyle E_{x}}$ ${\displaystyle x}$

Further definitions

The median is considered to be the most direct value for which

${\displaystyle P(X\leq m)={\frac {1}{2}}=P(X\geq m)}$

applies or defined. However, the existence of the median is not guaranteed in both definitions. So is for ${\displaystyle F^{-1}({\tfrac {1}{2}})}$

${\displaystyle P(X=0)=0{,}2=1-P(X=1)}$

always , since the distribution function never takes the value . Likewise, there is no , so the above chain of equations is satisfied: for all is , as for all still applies. ${\displaystyle F^{-1}({\tfrac {1}{2}})=\emptyset }$ ${\displaystyle {\tfrac {1}{2}}}$ ${\displaystyle m}$ ${\displaystyle m<1}$ ${\displaystyle P(X\leq m)<{\tfrac {1}{2}}}$ ${\displaystyle m\geq 1}$ ${\displaystyle P(X\leq m)=1}$

It should also be noted that the distribution functions in older Russian-language literature are defined as left-continuous and not as right-continuous as in the German-speaking area. For example, in the case of a fair coin toss, once instead of . ${\displaystyle F^{-1}({\tfrac {1}{2}})=(0,1]}$ ${\displaystyle F^{-1}({\tfrac {1}{2}})=[0,1)}$

Web links

• Median (in Statistics) . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
• VV Senatov: Quantiles . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
• Eric W. Weisstein : Statistical Median . In: MathWorld (English).

literature

• Christian Hesse : Applied probability theory . 1st edition. Vieweg, Wiesbaden 2003, ISBN 3-528-03183-2 , doi : 10.1007 / 978-3-663-01244-3 .
• Norbert Kusolitsch: Measure and probability theory . An introduction. 2nd, revised and expanded edition. Springer-Verlag, Berlin Heidelberg 2014, ISBN 978-3-642-45386-1 , doi : 10.1007 / 978-3-642-45387-8 .

Individual evidence

1. ^ Hans-Otto Georgii: Stochastics . Introduction to probability theory and statistics. 4th edition. Walter de Gruyter, Berlin 2009, ISBN 978-3-11-021526-7 , p. 101 , doi : 10.1515 / 9783110215274 .
2. ^ ^{A b} Hans-Otto Georgii: Stochastics . Introduction to probability theory and statistics. 4th edition. Walter de Gruyter, Berlin 2009, ISBN 978-3-11-021526-7 , p. 233 , doi : 10.1515 / 9783110215274 .
3. ↑ Norbert Kusolitsch: Measure and probability theory . An introduction. 2nd, revised and expanded edition. Springer-Verlag, Berlin Heidelberg 2014, ISBN 978-3-642-45386-1 , p. 113 , doi : 10.1007 / 978-3-642-45387-8 .