Molecular mechanics

from Wikipedia, the free encyclopedia
A force field is used to minimize the binding energy of this ethane molecule.

The molecular mechanism makes use of classical mechanics to molecular modeling systems. The potential energy of all systems is calculated in molecular mechanics using force fields . Molecular mechanics can be used to study small molecules, larger biological systems, for example channel proteins in cell membranes, and macromolecular constructs with thousands of atoms.

Fully atomistic methods have the following properties:

  • each atom is modeled as a single particle
  • each particle is assigned a radius (typically the van der Waals radius ), a polarizability, and a constant net charge
  • Binding interactions are treated as "springs" with an equilibrium deflection corresponding to the experimental or calculated binding length

Variations on this approach are possible; for example, some simulations have historically used a united-atom representation in which each methyl group is treated as a single particle. Large protein systems are mostly simulated using a spherical model in which two or four particles are assigned to each amino acid .

Functional form

Potential energy function in molecular mechanics.

The following functional abstraction, known as the potential energy function, or force field , calculates the potential energy of a molecular system in a given conformation as the sum of the individual energy terms:

where the components of the covalent and non-covalent contributions are given by:

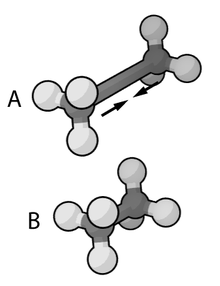
The exact functional form of the potential energy function, and thus the corresponding force field, depends on the simulation program used. In general, the bond and angle terms are modeled as harmonic potentials . The energy minima of these potentials are approximately the same as the bond lengths of the molecule, which are either determined experimentally or determined by software using ab initio methods. The Morse potential can be used for an accurate reproduction of the vibration spectra , but at the expense of the calculation effort. The dihedral and torsion terms typically have several minima and therefore cannot be modeled as harmonic oscillators. Dieder terms can intentionally contain “wrong” expressions that act as a correction for out-of-plane deviations (for example, to keep benzene rings planar, or to ensure correct geometry and chirality of tetrahedral atoms).

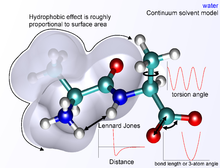
The non-bond terms are considerably more complex to calculate, since a typical atom is only directly (e.g. covalently) bound to a few partners, but actually interacts with every other atom in the molecule. Fortunately, the influence of the van der Waals term decreases rapidly with distance - it is usually modeled by a “6–12 Lennard-Jones potential ”, which means that attractive forces increase with distance with r −6 , and repulsive forces decrease with r −12 , where r is the distance between two atoms. The repulsive part r −12 is physically incorrect, however, since the repulsive force actually drops exponentially. The description of the van der Waals forces by “6–12 Lennard-Jones potentials” therefore contains inaccuracies that can become significant at short distances. Usually a cutoff radius is used to reduce the calculation time; interactions between atoms whose distance is above the cutoff radius are neglected.

The electrostatic terms are difficult to calculate because they don't decrease as quickly with increasing distance. Electrostatic interactions over long distances are often important influences on the system to be examined (especially for proteins ). The basic functional form is the Coulomb potential , which only drops with r −1 . A number of methods can be used to work around this problem; the simplest solution is a cutoff value as in the Van der Waals terms. However, this introduces a sharply delineated discontinuity between atoms inside and outside the cutoff radius, which is not desirable. This problem can be approached more precisely using switching or scaling functions that “hide” the apparent electrostatic energy by a continuous factor between 0 and 1 in the area of ​​the cutoff radius. Other, more differentiated, but also more calculation-intensive methods are known as particle mesh Ewald (PME) and the multipole algorithm .

In addition to the functional form of each energy term, parameters for force constants, van der Waals factors, and other constants must be assigned to a meaningful energy function. These constants, together with the equilibrium bond length, bond angle, dihedral angle, partial charges, atomic masses and radii and the definitions of the energy functions, are summarized under the term force field . The parameterization is typically done by matching empirical data and theoretically calculated values.

Each force field is parameterized so that it is internally consistent, but the parameters are generally not transferable from one field to another.

application areas

The main application of molecular mechanics is in the field of molecular dynamics simulation . This makes use of force fields to calculate the forces that act on each individual particle and thus to predict motion sequences. Provided that sufficient empirical data are available, thermodynamic or kinetic parameters such as the reaction speed can be estimated from the molecular dynamic motion sequences , assuming the ergodic hypothesis .

Another application of molecular mechanics is energy minimization, where force fields are used as optimization criteria. This method uses a suitable algorithm (e.g. the gradient method ) to find the molecular structure of a local energy minimum. These minima correspond to stable conformers of the molecule. Molecular motion can be modeled as vibrations around and interconversion between these stable conformers.

It is therefore common to combine methods for local energy minimization with those for global (within the scope of the simulation) energy optimization in order to find a general energy minimum. At limited (finite) temperatures, most of the time molecules exist in states that correspond to these energy minima, which makes them important for determining the molecular properties. Global optimization can be achieved through simulated annealing , the Metropolis algorithm, and other Monte Carlo simulations . Alternatively, various deterministic methods of discrete or continuous optimization can be used. While a force field only represents the enthalpic component of the Gibbs free energy , it is possible to include the entropic component through the use of additional methods, such as the analysis of vibrational modes .

Potential energy functions in molecular mechanics have already been used to determine binding constants, the kinetics of protein folding, proton equilibria, coordinates of molecular dockings , and protein binding sites .

Environment and Solvation

There are several ways to define the environment of a molecule. On the one hand, it can be modeled in a vacuum as a so-called gas phase simulation, whereby the environment is completely neglected. However, this is not desirable, since errors in the molecular geometry can occur, especially with charged compounds. Surface charges that would normally interact with molecules of the solvent instead interact with each other, creating conformations that are very improbable or impossible in actual environments. The "best" way to model solvation is to explicitly place solvent molecules in the simulation and not treat them differently from the molecule of interest itself.

As expected, the computational effort increases with the complexity of such a simulation. The complexity of models of water as a solvent, for example, ranges from being represented as a simple, hard sphere to four or five separate interaction points that even take into account the lone pairs of electrons in the oxygen atom.

A compromise between accuracy and computational effort can be achieved by implicit solvation , whereby the explicitly represented solvent molecules are replaced by mathematical expressions that approximate the behavior of the solvent. This method is useful to avoid the errors of a vacuum simulation, but it is not able to precisely represent the interactions between solvent and molecule of interest.

Examples of software packages

literature

Web links

Commons : Molecular Mechanics  - collection of images, videos, and audio files

Individual evidence

  1. ↑ Zgarbova M, et al .: Large-scale compensation of errors in pairwise-additive empirical force fields: comparison of AMBER intermolecular terms with rigorous DFT-SAPT calculations . In: Phys. Chem. Chem. Phys. . 12, 2010, pp. 10476-10493. bibcode : 2010PCCP ... 1210476Z . doi : 10.1039 / C002656E .
  2. ↑ Kuhn B, Kollman PA: Binding of a diverse set of ligands to avidin and streptavidin: an accurate quantitative prediction of their relative affinities by a combination of molecular mechanics and continuum solvent models . In: Journal of Medicinal Chemistry . 43, No. 20, October 2000, pp. 3786-91. doi : 10.1021 / jm000241h . PMID 11020294 .
  3. ↑ Huo S, Massova I, Kollman PA: Computational alanine scanning of the 1: 1 human growth hormone-receptor complex . In: J Comput Chem . 23, No. 1, January 2002, pp. 15-27. doi : 10.1002 / jcc.1153 . PMID 11913381 .
  4. ^ A b Mobley DL, Graves AP, Chodera JD, McReynolds AC, Shoichet BK, Dill KA: Predicting absolute ligand binding free energies to a simple model site . In: J Mol Biol . 371, No. 4, August 2007, pp. 1118-34. doi : 10.1016 / j.jmb.2007.06.002 . PMID 17599350 . PMC 2104542 (free full text).
  5. ↑ Wang J, Kang X, Kuntz ID, Kollman PA: Hierarchical database screenings for HIV-1 reverse transcriptase using a pharmacophore model, rigid docking, solvation docking, and MM-PB / SA . In: Journal of Medicinal Chemistry . 48, No. 7, April 2005, pp. 2432-44. doi : 10.1021 / jm049606e . PMID 15801834 .
  6. ↑ Kollman PA, Massova I, Reyes C, et al .: Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models . In: Acc Chem Res . 33, No. 12, December 2000, pp. 889-97. doi : 10.1021 / ar000033j . PMID 11123888 .
  7. ↑ Snow CD, Nguyen H, Pande VS, Gruebele M: Absolute comparison of simulated and experimental protein-folding dynamics . In: Nature . 420, No. 6911, November 2002, pp. 102-6. bibcode : 2002Natur.420..102S . doi : 10.1038 / nature01160 . PMID 12422224 .
  8. ^ Barth P, Alber T, Harbury PB: Accurate, conformation-dependent predictions of solvent effects on protein ionization constants . In: Proc Natl Acad Sci USA . 104, No. 12, March 2007, pp. 4898-903. bibcode : 2007PNAS..104.4898B . doi : 10.1073 / pnas.0700188104 . PMID 17360348 . PMC 1829236 (free full text).
  9. ↑ Chakrabarti R, Klibanov AM, Friesner RA: Computational prediction of native protein ligand-binding and enzyme active site sequences . In: Proc Natl Acad Sci USA . 102, No. 29, July 2005, pp. 10153-8. bibcode : 2005PNAS..10210153C . doi : 10.1073 / pnas.0504023102 . PMID 15998733 . PMC 1177389 (free full text).
  10. ↑ Boas FE, Harbury PB: Design of Protein-Ligand Binding Based on the Molecular-Mechanics Energy Model . In: J Mol Biol . 380, No. 2, July 2008, pp. 415-24. doi : 10.1016 / j.jmb.2008.04.001 . PMID 18514737 . PMC 2569001 (free full text).