Ovoid (Projective Geometry)

To define an ovoid:
t tangent, s secant

In projective geometry, an ovoid is a ball-like set of points (surface) in a projective space of dimension . An ovoid is the spatial analog of an oval in a projective plane . The simplest examples in real projective spaces are hyperspheres ( quadrics ). ${\displaystyle n\geq 3}$

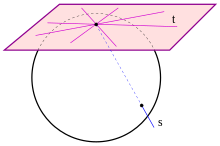
The essential geometric properties of an ovoid are: 1) A straight line meets at most 2 points , 2) The tangents in one point cover a hyperplane (and no more), 3) Contains no straight lines. Property 2) excludes degenerate cases ( cones , ...). Property 3) excludes ruled surfaces (e.g. single-shell hyperboloids ). ${\displaystyle {\mathcal {O}}}$ ${\displaystyle {\mathcal {O}}}$ ${\displaystyle {\mathcal {O}}}$

On the one hand, the fact that there are no non-Desarguean projective spaces makes the discussion in relation to the flat case (there are non-Desarguean levels) easier, on the other hand, there is not one in every pappus space (projective space above a body) Quadric, which is an ovoid. (But in every pappus plane there are oval conic sections !)

An ovoid is a special square set by definition .

Ovids play an essential role in the construction of Möbius levels or Möbius rooms.

Definition of an ovoid

• A set of points in a projective space of dimension is called an ovoid if: ${\displaystyle {\mathcal {O}}}$ ${\displaystyle \geq 3}$

(1) Any straight line hits a maximum of 2 points. If is, is called passer , if is, is called tangent and if is, is called secant . ${\displaystyle g}$ ${\displaystyle {\mathcal {O}}}$
${\displaystyle |g\cap {\mathcal {O}}|=0}$ ${\displaystyle g}$ ${\displaystyle |g\cap {\mathcal {O}}|=1}$ ${\displaystyle g}$ ${\displaystyle |g\cap {\mathcal {O}}|=2}$ ${\displaystyle g}$

(2) The following applies for each point : The tangents in cover exactly one hyperplane, the tangential hyperplane, (projective subspace of the dimension ). ${\displaystyle P\in {\mathcal {O}}}$ ${\displaystyle P}$ ${\displaystyle n-1}$

(3) does not contain any straight lines. ${\displaystyle {\mathcal {O}}}$

An ovoid is a homogeneous structure with regard to the hyperplane cuts, because it applies

• If there is an ovoid and a hyperplane that contains at least 2 points of , then an ovoid (oval, if d = 3) is in the hyperplane . ${\displaystyle {\mathcal {O}}}$ ${\displaystyle \varepsilon }$ ${\displaystyle {\mathcal {O}}}$ ${\displaystyle \varepsilon \cap {\mathcal {O}}}$ ${\displaystyle \varepsilon }$

For finite projective spaces of dimension (i.e. set of points and set of lines are finite, the space can be coordinated over a body): ${\displaystyle d\geq 3}$

• If an ovoid is in a finite projective space of dimension , then is . ${\displaystyle {\mathcal {O}}}$ ${\displaystyle d\geq 3}$ ${\displaystyle {\color {red}d=3}}$

(So ​​in the finite case there are ovaries only in 3-dimensional space!)

• In a projective space of order (i.e. every straight line contains points) and dimension , a set of points is an ovoid if and only if is and no three points are collinear (on a straight line). ${\displaystyle n>2}$ ${\displaystyle n+1}$ ${\displaystyle d={\color {red}3}}$ ${\displaystyle {\mathcal {O}}}$ ${\displaystyle |{\mathcal {O}}|=n^{2}+1}$ ${\displaystyle {\mathcal {O}}}$

If the word projective is replaced by affine in the definition, one obtains the definition of an affine ovoid.

If there is a passing hyperplane for a (projective) ovoid, this can be explained as a remote hyperplane and the ovoid is an affine ovoid in the associated affine space. Conversely, every affine ovoid in the projective closure (adding a remote hyperplane) is a (projective) ovoid.

Examples

In real projective space (inhomogeneous representation)

1. ${\displaystyle {\mathcal {O}}=\{(x_{1},...,x_{d})\in \mathbb {R} ^{d}\;|\;x_{1}^{2}+\cdots +x_{d}^{2}=1\}\ ,}$ (Hyper sphere)
2. ${\displaystyle {\mathcal {O}}=\{(x_{1},...,x_{d})\in \mathbb {R} ^{d}\;|x_{d}=x_{1}^{2}+\cdots +x_{d-1}^{2}\;\}\;\cup \;\{{\text{Fernpunkt der }}x_{d}{\text{-Achse}}\}}$

The two examples are quadrics and projectively equivalent. (See also the examples in Oval .)

As with ovals, here are simple examples that are not squares:

(a) Put half a hypersphere and half a hyperellipsoid together smoothly.

(b) Replace the term with in the first two examples . ${\displaystyle x_{1}^{2}}$ ${\displaystyle x_{1}^{4}}$

Note: The real examples cannot be transferred to the complex case (spaces over ). In complex projective spaces of dimension there are no ovoid quadrics. In the complex case there are always straight lines on a non-degenerate quadric. ${\displaystyle \mathbb {C} }$ ${\displaystyle d\geq 3}$

But the following applies:

• Ovoids can be detected in every non-finite projective space with the help of transfinite induction .

Finite examples

• If an ovoid is in a finite projective space of dimension over a body of characteristic , then it is a quadric. ${\displaystyle {\mathcal {O}}}$ ${\displaystyle d=3}$ ${\displaystyle K}$ ${\displaystyle {\color {red}\neq }2}$ ${\displaystyle {\mathcal {O}}}$

The following examples show that the last result is wrong in the even case:

• Let it be odd and the automorphism ${\displaystyle K=GF(2^{m}),\;m}$ ${\displaystyle \sigma }$ ${\displaystyle x\mapsto x^{(2^{\frac {m+1}{2}})}\;.}$

Then

${\displaystyle {\mathcal {O}}=\{(x,y,z)\in K^{3}\;|\;z=xy+x^{2}x^{\sigma }+y^{\sigma }\}\;\cup \;\{{\text{Fernpunkt der }}z{\text{-Achse}}\}}$an ovoid in 3-dimensional projective space over (in inhomogeneous coordinates). ${\displaystyle K}$

${\displaystyle {\mathcal {O}}}$is a quadric only in the case . ${\displaystyle m=1}$

${\displaystyle {\mathcal {O}}}$is called Tits-Suzuki-Ovoid .

When is an ovoid a quadric?

An ovoid quadric is characterized by a particularly large number of symmetries. The following applies:

• Let it be an ovoid in a projective space and a hyperplane of an at least 2-dimensional desargue projective space (in the 2-dimensional case is an oval) of the characteristic . If the ovoid lies symmetrically to each point (i.e. there is an involutorial perspective with a center that leaves invariant), then it is pappus and a quadric. ${\displaystyle {\mathcal {O}}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle \varepsilon }$ ${\displaystyle {\mathcal {O}}}$ ${\displaystyle \neq 2}$ ${\displaystyle P\in \varepsilon \setminus {\mathcal {O}}}$ ${\displaystyle P}$ ${\displaystyle {\mathcal {O}}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle {\mathcal {O}}}$

• An ovoid in a pappus projective space is a quadric if the group of projectivities that leave invariant operates on 3-fold transitive operations, i.e. H. to 2 triples of points there is a projectivity with . ${\displaystyle {\mathcal {O}}}$ ${\displaystyle {\mathcal {O}}}$ ${\displaystyle {\mathcal {O}}}$ ${\displaystyle A_{1},A_{2},A_{3},\;B_{1},B_{2},B_{3}}$ ${\displaystyle \pi }$ ${\displaystyle \pi (A_{i})=B_{i},\;i=1,2,3}$

In the finite case it follows from Segre's theorem :

• Let it be an ovoid in a finite, desargue, projective 3-dimensional space of odd order. Then pappussch and a quadric. ${\displaystyle {\mathcal {O}}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle {\mathfrak {P}}}$ ${\displaystyle {\mathcal {O}}}$

Generalization: semi-ovoid

If one omits condition (1) when defining an ovoid, one obtains the definition of a hemovoid:

A set of points of a projective space is Halbovoid (engl .: semi ovoid ) if: ${\displaystyle {\mathcal {O}}}$

(HO1) The following applies for each point : The tangents (straight lines that have only one point in common) cover exactly one hyperplane. ${\displaystyle P\in {\mathcal {O}}}$ ${\displaystyle {\mathcal {O}}}$ ${\displaystyle P}$

(HO2) does not contain any straight lines. ${\displaystyle {\mathcal {O}}}$

Half has no quantitative meaning here, but means weaker conditions.

A semi-ovoid is a special Hermitian set ( semi quadratic set ) that is a generalization of the quadratic set . The property that distinguishes a Hermitian from a quadratic set is that a straight line with a Hermitian set can have more than 2 points in common without it being completely contained.

Examples of hemovoids are isotropic point sets of Hermitian shapes , so-called Hermitian quadrics .

In the literature, criteria can also be found for hemovoid as to when a hemovoid is a Hermitian quadric . (e.g.)

Semovovids are used analogously to the ovoidal Möbius planes for the construction of Möbius geometries.

Web links

• E. Hartmann: Planar Circle Geometries, an Introduction to Moebius, Laguerre and Minkowski Planes. Script, TH Darmstadt (PDF; 891 kB), pp. 121–123.

See also

• Oval (projective geometry)
• Möbius level

Individual evidence

1. ^ P. Dembowski : Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8 , p. 28
2. ^ P. Dembowski : Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8 , p. 48
3. ^ P. Dembowski : Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8 , p. 48
4. ^ W. Heise: Report on -affine geometries ${\displaystyle \kappa }$ , Journ. of Geometry 1 (1971), pp. 197-224, sentence 3.4.
5. ^ P. Dembowski : Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8 , p. 49
6. ^ P. Dembowski : Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8 , p. 52
7. ↑ H. Mäurer: Ovoide with symmetries at the points of a hyperplane , Abh. Math. Sem. Hamburg 45 (1976), pp. 237-244
8. ↑ J. Tits : Ovoides à Translations , Rend. Mat. 21 (1962), pp. 37-59.
9. ^ F. Buekenhout : A Characterization of Semi Quadrics , Atti dei Convegni Lincei 17 (1976), pp. 393-421.
10. ^ KJ Dienst: Identification of Hermitian Quadrics by Reflections , Contributions to Geometric Algebra (1977), Birkhäuser-Verlag, pp. 83-85.