Precision rectifier

A precision rectifier is an electronic circuit that takes on the function of a rectifier without the usual defects of real diodes . Such circuits for small alternating voltages are required and in use in electrical measurement technology in particular .

Real diode

Silicon small signal diodes 1N4148
max. 75 or 100 V reverse voltage (depending on data sheet),
max. 200 mA forward current,
max. 4 ns blocking recovery time

Small-signal silicon diodes can only be used to a limited extent for measurement purposes; however, there is no better component for this purpose. The two fundamental deviations from the ideal static behavior (guide values ​​in brackets at 25 ° C for types 1N4148 and 1N914) are:

* Reverse current ${\displaystyle I_{R}}$	(<25 nA)
* Forward voltage ${\displaystyle U_{F}}$	(≈ 0.7 V, depending on the current strength)

The reverse current can usually be ignored as the cause of measurement deviations , but the forward voltage has a very falsifying effect, especially since the relationship between forward voltage and forward current is highly non-linear and temperature-dependent.

There are no deviations from the ideal dynamic behavior of these diodes for the measurement tasks dealt with here.

Circuit variants

Half-wave rectifier

With the help of feedback operational amplifiers , real diodes can be operated in such a way that the circuit behaves like an ideal diode. The diode continues to perform rectification, while the operational amplifier compensates for the forward voltage of the diode by increasing the voltage at its output.

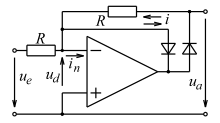
Simple half-wave rectifier

One-way precision rectifier

A simple precision rectifier circuit consists of an operational amplifier with a diode and a resistor in series at the output, as shown in the figure opposite. In this circuit, a negative input voltage causes the diode to block and the output voltage to remain at 0 V. With a positive input voltage is the same . ${\displaystyle u_{e}}$ ${\displaystyle u_{a}}$ ${\displaystyle u_{a}}$ ${\displaystyle u_{e}}$

The disadvantage of this simple circuit is that if the input voltage is negative, the blocking diode will interrupt the negative feedback at the operational amplifier. This leads to the fact that the output voltage in the operational amplifier is driven into the limit, from which it comes out with a time delay when the input voltage becomes positive again later. This poor time behavior leads to mapping errors and reduces the bandwidth , especially with low input voltages. Furthermore, asymmetrical AC voltage waveforms are not displayed correctly, since only the positive half-wave is taken into account.

Improved half-wave rectifier

Precision half-wave rectifier

With the almost always permissible approximations of the ideal operational amplifier that is not overdriven

${\displaystyle u_{d}=0\quad ;\qquad i_{n}=0}$

the measuring circuit generates a voltage signal from the input voltage ${\displaystyle u_{e}}$

${\displaystyle u_{a}={\begin{cases}|u_{e}|&{\text{wenn }}u_{e}<0\\\ 0&{\text{wenn }}u_{e}>0\end{cases}}}$

regardless of the forward voltage , even if is. ${\displaystyle U_{F}}$ ${\displaystyle |u_{e}|<U_{F}}$

With this circuit, one of the two diodes is always conductive, depending on the polarity of the input voltage. This avoids overloading and saturation of the operational amplifier, which significantly improves the time response. Since the operational amplifier also has to build up the forward voltage of the diodes , a change in polarity of the input voltage at the output of the operational amplifier leads to voltage jumps of around twice the forward voltage of the diodes. Why should primarily at small input signals operational amplifier with the highest possible voltage slew rate ( slew rate ) are used. ${\displaystyle u_{a}}$ ${\displaystyle {\tfrac {\mathrm {d} u}{\mathrm {d} t}}}$

By changing the polarity of both diodes in the circuit, either the positive or negative half-oscillation can be evaluated.

Full wave rectifier

Adding circuit

Precision full-wave rectifier consisting of a half-wave rectifier and adder

There are several ways to implement a precision full-wave rectifier. The best-known solution is to expand the precision half-wave rectifier with a downstream inverting adding circuit with an additional operational amplifier, as shown in the adjacent circuit.

The input voltage is fed to one input of the addition stage with the resistor . The output voltage of the half-wave rectifier is fed to the other input of the addition stage with the resistor . As in the previous circuit, the same applies to both operational amplifiers ${\displaystyle R_{3}}$ ${\displaystyle u_{e}}$ ${\displaystyle R_{4}}$ ${\displaystyle u_{g}}$ ${\displaystyle u_{d}=0\;;\;i_{n}=0.}$

If the input voltage is negative , D2 is blocked, no current flows through ; . This means that no current flows through either . Since the voltage must be zero at the input of the second operational amplifier , a positive voltage must arise at the output of the addition stage . Additionally with must adjust. ${\displaystyle R_{2}}$ ${\displaystyle u_{g}=0}$ ${\displaystyle R_{4}}$ ${\displaystyle u_{d}=0}$ ${\displaystyle i_{n}=0}$ ${\displaystyle {\frac {u_{a}}{R_{5}}}+{\frac {u_{e}}{R_{3}}}=0}$

If the input voltage is positive , D2 is conductive, current flows through it; the tension becomes negative . The first amplifier appears . The same applies to the input of the second operational amplifier ${\displaystyle R_{2}}$ ${\displaystyle u_{g}}$ ${\displaystyle {\frac {u_{e}}{R_{1}}}+{\frac {u_{g}}{R_{2}}}=0}$ ${\displaystyle {\frac {u_{a}}{R_{5}}}+{\frac {u_{e}}{R_{3}}}+{\frac {u_{g}}{R_{4}}}=0.}$

This is simplified with the dimensioning : ${\displaystyle R_{1}=R_{2}=R_{3}=R_{5}=2\,R_{4}}$

* at ${\displaystyle u_{e}\leq 0}$	${\displaystyle u_{g}=0\ ;}$	${\displaystyle u_{a}=-u_{e}}$
* at ${\displaystyle u_{e}\geq 0\qquad }$	${\displaystyle u_{g}=-u_{e}\ ;\quad }$	${\displaystyle u_{a}=-u_{e}-2\,u_{g}=-u_{e}+2\,u_{e}=u_{e}}$

The amount of the input voltage appears at the output at all times. The full wave rectifier thus has the transfer function

${\displaystyle u_{a}=|u_{e}|}$.

The forward voltage is not included in the output signal of the rectifier circuit in that it is used instead as the output voltage. The amplifier only needs to be able to build up a higher voltage at its output . ${\displaystyle u_{g}}$ ${\displaystyle u_{a1}}$ ${\displaystyle U_{F}}$

The feedback resistance can be changed without affecting the function to adjust the overall gain. If, for example, the mentioned resistance is increased to 1.11 times the value, then the equivalent value of the output voltage is as large as the effective value of a sinusoidal input voltage. ${\displaystyle R_{5}}$

The output voltage is load-independent within the framework of the load capacity of the second operational amplifier. ${\displaystyle u_{a}}$

Bridge rectification

Precision bridge rectifier

The adjacent measuring circuit generates a current signal

${\displaystyle i_{a}=|u_{e}|/R}$

independent of and from the internal resistance of the ammeter . ${\displaystyle U_{F}}$

The circuit behaves within certain limits like a controlled ideal current source . The output current is proportional to the amount of the input voltage.

A disadvantage of the bridge rectifier circuit is that none of the connection points of the measuring device has the same potential as one of the connection points of the input voltage. A sequential circuit instead of the measuring device for further processing of the rectified current obtained in this way must be potential-free in relation to the input voltage.

Applications

Precision rectifiers are used, for example, to calculate the amount of alternating quantities in multimeters in the frequency range of analog audio technology . With batteryless current and voltage measuring devices , the distortion by passive diode measuring rectifiers is compensated by a non-linear scale division in the lower range in the alternating quantity measuring ranges . The use of a precision rectifier allows a linear division through to the zero point and the measurement of smaller voltages.

Precision half-wave rectifier for the measurement of alternating quantities for linear scale division despite non-linear diode characteristic

The adjacent measuring circuit shows a precision half-wave rectifier in an analog multimeter as an example . With the characteristics of the operational amplifier

${\displaystyle u_{d}=0\quad ;\quad i_{e}=0}$

applies:

${\displaystyle i_{a}=i_{m}={\frac {u_{m}}{R_{m}}}}$

During the positive half-oscillation of the current flows through the measuring mechanism; during the negative half-oscillation also flows , but bypasses the measuring mechanism. In the case of a sinusoidal input voltage with the amplitude , a moving - coil measuring mechanism that forms the equivalent results in a display of half the rectified value ${\displaystyle i_{a}}$ ${\displaystyle i_{a}}$ ${\displaystyle {\hat {u}}_{m}}$

${\displaystyle I_{\mathrm {Anzeige} }={\frac {1}{2}}\;{\overline {|i_{a}|}}={\frac {1}{\pi }}\cdot {\frac {{\hat {u}}_{m}}{R_{m}}}}$

The problem that a statement about the effective value of the measurable rectified value is only possible if the curve shape is known remains unaffected by the precision of the rectification.

literature

• Paul Horowitz, Winfield Hill: The Art of Electronics . 2nd Edition. Cambridge Press, 1989, ISBN 0-521-37095-7 , pp. 221-222 .
• Erwin Böhmer: Elements of Applied Electronics . Min. 16 editions since 1979, Vieweg;
  now by Erwin Böhmer, Dietmar Ehrhardt, Wolfgang Oberschelp.

Individual evidence

1. ↑ For example, fast universal diode 1N914 for electronics, data sheet [1]
2. ↑ ^{a b c} Klaus Bystron, Johannes Bergmeyer: Fundamentals of technical electronics . Hanser, 1988, p. 343 f
3. ↑ Ekbert Hering, Jürgen Gutekunst, Rolf Martin: Electrical engineering for mechanical engineers: Fundamentals. Springer, 1999, p. 196
4. ^ Albert Haug: Microelectronics and microprocessors for mechanical engineers. Vieweg, 1987, p. 187