Riemann-Siegel theta function
The Riemann-Siegel theta function is a special function from analytical number theory , a branch of mathematics. It is primarily used to investigate the zeros of the Riemann zeta function and thus as a tool in connection with the Riemann Hypothesis , a problem in mathematics that has not yet been solved , the solution of which would allow statements about the distribution of prime numbers . With the help of the Riemann-Siegel theta function, the number of so-called non-trivial zeros of the Riemann zeta function can be specified up to a given imaginary part. The Riemann-Siegel theta function also appears in the definition of Gram points - certain real numbers whose position often, but not always, limits the position of those zeros.
The theta function is named after the two German mathematicians Bernhard Riemann and Carl Ludwig Siegel . Riemann, who died in 1866 at the age of 39, left numerous private worksheets and mathematical notes. Siegel, born in 1896, took on these documents and in 1932 published a paper on Riemann's estate on analytical number theory. There he dealt with the now so called Riemann-Siegel formula and thus also the theta function.
The Riemann-Siegel theta function presented in this article must be distinguished from other mathematical functions that are also called “theta functions”, such as the Jacobian or Ramanujan theta function .
definition
The Riemann-Siegel theta function is defined for real things by
- .
Here referred to the circle number , the imaginary unit , the logarithm function , the gamma function and an argument function that is clearly defined by the following conditions: The values of the argument function must be determined so that true and a continuous function is.
This definition can also be in the form
if you choose the main branch of the logarithm and denote the imaginary part of a complex number .
This last form of definition is also suitable for defining the Riemann-Siegel theta function for complex arguments :
where the main branch of the logarithm is to be selected.
Properties of the theta function with real argument
Curve discussion
The Riemann-Siegel theta function with a real argument is a real analytic function . In particular, it can be differentiated continuously and any number of times . Such as B. the sine function it belongs to the odd functions . So it applies to everyone . In addition to the 0, it also has the two zeros
The real argument theta function takes in
a local minimum or maximum . The function values there are
For positive, growing goes against ; for negative, shrinking against .
Asymptotic development
The Riemann-Siegel theta function with a real argument has an asymptotic expansion , the leading terms of which have the following form:
When deriving this development, the function is replaced by its Stirling series in the definition of and an identity is used between the complex logarithm and the arctangent and its series representation. For larger values of , the asymptotic expansion truncated after the term already provides good approximations of the actual values of . So it applies
- .
If necessary, the quality of this approximation can be increased with the help of further elements of the asymptotic development.
Connection with the Riemann zeta function

The Riemann zeta function is one of the most important functions of analytic number theory. It owes its paramount importance to the connection between the position of its complex zeros and the distribution of the prime numbers . Its so-called trivial zeros are the negative even numbers, i.e. −2, −4, −6, −8 etc. In addition, it also has an infinite number of so-called non-trivial zeros, whose real parts are known to lie between 0 and 1. In his famous work from 1859, Bernhard Riemann suggested that all non-trivial zeros of the zeta function have the real part 1/2. This thesis, which has not been proven or refuted to this day, is known as the Riemann Hypothesis .
With a view to the Riemann Hypothesis, one tries first to obtain statements about zeros of the zeta function with real part 1/2. It turns out to be advantageous not to work directly with the Riemann zeta function , but with a close relative: the Riemann Xi function . This is defined for complex by
On the right-hand side, the factors in front of the zeta function precisely eliminate the trivial zeros of the zeta function and their poles in 1. Thus the zeros of the Xi function are identical to the nontrivial zeros of the zeta function. Compared to the Riemann zeta function but the function Xi has now the advantage on the so-called critical line , to assume only real values. Therefore, one can find simple zeros of the Xi function with real part 1/2 and thus non-trivial zeros of the zeta function with real part 1/2 by checking for sign changes along the critical straight line. These are employed in one. By simple transformations one is led not only to the definition of the Riemann-Siegel theta function, but also to the definition of the Riemann-Siegel Z function :
It denotes the real part of a complex number. As for the question of the change in sign of along the critical straight line, the expression within the first pair of square brackets always gives a negative real value for each real value. Further details of this expression do not need to be examined in connection with the required sign changes. The function within the second pair of square brackets is exactly the Riemann-Siegel Z-function, which is also called Hardy's Z-function after the British mathematician Godfrey Hardy :
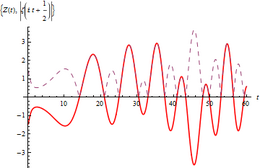
For further simplification, the two factors now urge the definition of a further function, namely the Riemann-Siegel theta function
because with their help then applies
In summary it now results:
When looking for a change of sign of the Xi function and thus for zeros of the zeta function on the critical straight line, the last equation does not appear to be very useful at first glance, since the value of is expressed with the help of . However, the value of good can be approximated without having to calculate the function value. The Riemann-Siegel formula is used for this
in which denotes a natural number and the cosine function . In the Riemann-Siegel formula, the value of depends only on and the selected , but no longer on . This also applies to the error term. With the help of the theta function and the Riemann-Siegel formula, approximations of the values of and thus the change in sign of can be determined. These sign changes indicate simple zeros of the Xi function on the critical straight line and thus zeros of the zeta function with real part 1/2.
Number of non-trivial zeros of the Riemann zeta function
If a positive real number, one denotes the number of all zeros of the Riemann zeta function with and . The value of indicates the number of non-trivalent zeros of the zeta function with a positive imaginary part in the so-called critical strip , which is defined as the set of complex numbers with a real part . The zeros are counted according to their multiples , with only non-trivial zeros with simple multiplicity being found so far.
If there is no imaginary part of a non-trivial zero of the zeta function, the value of exactly can be specified with the aid of the Riemann-Siegel theta function and an error function :
Since the error function grows much more slowly for things that get larger than , the value of is approximately exactly the same .
Grief points


The real zeros of the function are called Gram points . So if a real number is with , then a Gram point is called, named after the Danish mathematician Jørgen Pedersen Gram . Since the sine function takes its zeros in integer multiples of , a real one is a gram point if and only if
applies to a .
Gram points are usually numbered according to the following scheme: Because of this , the three real zeros of the theta function are obviously gram points. The largest of these zeros in is given the number 0 and is sometimes referred to as. Larger gram points are numbered in ascending order according to their size; smaller grief points in descending order. The following table shows the first, non-negative Gram points using this numbering:
| −3 | 0 | 0 |
| −2 | 3.4362182261 ... | −π |
| −1 | 9.6669080561 ... | −π |
| 0 | 17.8455995405… | 0 |
| 1 | 23.1702827012 ... | π |
| 2 | 27.6701822178 ... | 2π |
| 3 | 31.7179799547 ... | 3π |
| 4th | 35.4671842971 ... | 4π |
| 5 | 38.9992099640 ... | 5π |
| 6th | 42.3635503920 ... | 6π |
| 7th | 45.5930289815 ... | 7π |
| 8th | 48.7107766217… | 8π |
| 9 | 51.7338428133… | 9π |
| 10 | 54.6752374468 ... | 10π |
| 11 | 57.5451651795… | 11π |
| 12 | 60.3518119691… | 12π |
| 13 | 63.1018679824 ... | 13π |
| 14th | 65.8008876380 ... | 14π |
| 15th | 68.4535449175… | 15π |
If one now compares the Gram points with small numbers with the imaginary parts of the zeros of the Riemann zeta function along the critical straight line , these alternate. The wrong thesis that Gram points alternated with the imaginary parts of these zeros for all of them was misleadingly called Grams law by the American mathematician John Irwin Hutchinson . The first of the infinitely many counterexamples to this “law” can be found in the interval between the grief points
and
- :
This interval does not contain an imaginary part of a zero of the Riemann zeta function. However, the following imaginary part of the zero just misses this interval.
literature
Mathematical textbooks on the Riemann zeta function and the Riemann Hypothesis usually contain a representation of the Riemann-Siegel theta function. Most of these textbooks were written in English. Titchmarsh's book is a classic and still widely cited textbook. However, it does not contain an index and does not correspond to the form of presentation of mathematical textbooks that is usual today - in contrast to the books by Ivić, Karatsuba and Voronin. The book by Borwein et al. provides a concentrated summary of the fundamental properties of the Riemann zeta function and related functions on the first pages, while the rest of the book contains original mathematical works. The approach in Edwards' book is the explanation of mathematics in Bernhard Riemann's 1859 article.
- Peter Borwein , Stephen Choi, Brendan Rooney, Andrea Weirathmueller: The Riemann Hypothesis . Springer, New York 2008, ISBN 978-0-387-72125-5 (Section 3.5).
- Harold Edwards : Riemann's Zeta Function . Dover, Mineola 2001, ISBN 0-486-41740-9 (Section 6.5).
- Wolfgang Gabcke: New derivation and explicit residual estimate of the Riemann-Siegel formula. Dissertation Univ. Göttingen, 1979. Revised version (eDiss Göttingen 2015).
- Aleksandar Ivić : The Riemann Zeta-Function. Theory and Applications . Dover, Mineola 2003, ISBN 0-486-42813-3 (Chapter 10).
- Aleksandar Ivić: The Theory of Hardy's Z-Function . Cambridge University Press, New York 2013, ISBN 978-1-107-02883-8 (covers Hardy's Z function in detail and therefore also the Riemann-Siegel theta function).
- Anatoly A. Karatsuba , Sergei M. Voronin : The Riemann Zeta-Function . Walter de Gruyter, Berlin 1992, ISBN 3-11-013170-6 (Chapter 3, Paragraph 4).
- Bernhard Riemann : About the number of prime numbers under a given size . In: Monthly reports of the Royal Prussian Academy of Sciences in Berlin . Berlin 1859, p. 671-680 .
- Carl Ludwig Siegel : About Riemann's papers on analytical number theory. Sources and studies on the history of mathematics, astronomy and physics, Dept. B: Studies 2 . 1932, p. 45-80 .
- Edward Charles Titchmarsh : The Theory of the Riemann Zeta-Function . Oxford University Press, New York 2007, ISBN 978-0-19-853369-6 (first edition: 1951, reprint, sections 4.17, 9.2, 9.3, 9.4 and 10.6).
Web links
- Eric W. Weisstein : Riemann-Siegel Functions . In: MathWorld (English).
Individual evidence
- ↑ Harold Edwards : Riemann's Zeta Function. Dover, Mineola 2001, ISBN 0-486-41740-9 , Section 7.1, pp. 136 and 137. (English).
- ^ A b c d Andrew Odlyzko: On the Distribution of Spacings Between Zeros of the Zeta Function. In: Mathematics of Computations. Volume 48, No. 117, 1987, p. 276 (English).
- ^ Peter Borwein et al .: The Riemann Hypothesis. Springer, New York 2008, ISBN 978-0-387-72125-5 , section 3.3, p. 32 (English).
- ↑ Aleksandar Ivić : The Theory of Hardy's Z-Function. Cambridge University Press, New York 2013, ISBN 978-1-107-02883-8 , Notation Section, p. Xvi. (English).
- ↑ functions.wolfram.com: RiemannSiegelTheta. Definition of the Riemann-Siegel theta function.
- ↑ On-Line Encyclopedia of Integer Sequences : Sequence A114857. Decimal expansion of the 0th gram point, i.e. the largest real zero of the theta function.
- ↑ On-Line Encyclopedia of Integer Sequences: Sequence A114866. Decimal expansion of the position of the unique, local minimum of the Riemann-Siegel theta function.
- ↑ On-Line Encyclopedia of Integer Sequences: Sequence A114865. Decimal expansion of the value of the unique, local maximum of the Riemann-Siegel theta function.
- ↑ a b Harold Edwards: Riemann's Zeta Function. Dover, Mineola 2001, ISBN 0-486-41740-9 , Section 6.5, p. 120 (English).
- ↑ On-Line Encyclopedia of Integer Sequences: Sequence A036282. Numerator of the asymptotic expansion of the theta function.
- ↑ On-Line Encyclopedia of Integer Sequences: Sequence A114721. Denominator of the asymptotic expansion of the theta function.
- ↑ Harold Edwards: Riemann's Zeta Function. Dover, Mineola 2001, ISBN 0-486-41740-9 , Section 6.5, pp. 119 and 120 (English).
- ↑ Harold Edwards: Riemann's Zeta Function. Dover, Mineola 2001, ISBN 0-486-41740-9 , Section 6.3, p. 109 (English).
- ↑ a b Anatoly A. Karatsuba , Sergei M. Voronin : The Riemann Zeta-Function. Walter de Gruyter, Berlin 1992, ISBN 3-11-013170-6 , Chapter I, Paragraph 6, Section 1, Theorem 1, p. 22 (English).
- ↑ a b Peter Borwein et al .: The Riemann Hypothesis. Springer, New York 2008, ISBN 978-0-387-72125-5 , section 3.3, p. 31 (English).
- ^ Edward C. Titchmarsh : The Theory of the Riemann Zeta Function. Oxford University Press, New York 1951, Reprint 2007, ISBN 978-0-19-853369-6 , Section 9.2, p. 211 (English).
- ↑ Harold Edwards: Riemann's Zeta Function. Dover, Mineola 2001, ISBN 0-486-41740-9 , Section 6.5, p. 125 (English).
- ^ Peter Borwein et al .: The Riemann Hypothesis. Springer, New York 2008, ISBN 978-0-387-72125-5 , section 3.5, p. 33 (English).
- ^ John Irwin Hutchinson : On the roots of the Riemann zeta function. In: Trans. Amer. Math. Soc. Volume 27, pp. 49-60, 1925, regarding Grams law see p. 52 (English).
Remarks
- ↑ The gamma function has poles at all non-positive, integers, i.e. in 0, −1, −2, −3 etc. In the definition of the theta function with real , however, this does not pose a problem, since the expression then has these values does not accept. Rather, they are in , in order that vertical line in the complex plane, passing through the point extends.
- ↑ Aside from its poles, the gamma function delivers complex, also non-real, numbers as function values. Arguments of complex numbers other than 0 are always real. Since the expression for real is real anyway, the theta function with real argument is a real-valued function.
- ↑ Arguments of complex numbers not equal to 0 are only unique up to integer multiples of . For is and a real number. Therefore the condition means that the value 0 is to be chosen for the argument of , and not or or any other integer multiple of different from 0 .
- ↑ The continuity condition is fulfilled for the partial function, since it is a straight line. The gamma function is holomorphic apart from its poles , i.e. especially continuous. This means that it is also continuous along the straight line . Starting from the definition , that is , the values of the argument function can always be chosen so that the function and thus become continuous, and those values are uniquely determined by this continuity condition.
-
↑ Logarithms of complex numbers not equal to 0 are only unique up to integer multiples of . The definition of the main branch of the logarithm leads to the fact that is continuous and for :
- .
- ↑ Instead of , the critical strip is often defined as the set of all complex numbers with a real part , since according to the prime number theorem there are no zeros of the zeta function on the two vertical straight lines through 0 and 1, respectively. It is known that these two lines are not “critical”. Therefore, they can be dispensed with when defining the critical strip.




































![{\ displaystyle {\ begin {aligned} \ xi \ left ({\ frac {1} {2}} + it \ right) & = {\ frac {1} {2}} \ left ({\ frac {1} {2}} + it \ right) \ left (- {\ frac {1} {2}} + it \ right) \ pi ^ {- {\ frac {1} {4}} - {\ frac {it} {2}}} \, \ Gamma \ left ({\ frac {1} {4}} + {\ frac {it} {2}} \ right) \ zeta \ left ({\ frac {1} {2} } + it \ right) \\ & = - {\ frac {1} {2}} \ left ({\ frac {1} {4}} + t ^ {2} \ right) \ pi ^ {- {\ frac {1} {4}} - {\ frac {it} {2}}} \, \ Gamma \ left ({\ frac {1} {4}} + {\ frac {it} {2}} \ right ) \ zeta \ left ({\ frac {1} {2}} + it \ right) \\ & = \ left [- {\ frac {1} {2}} \ cdot e ^ {\ operatorname {Re} \ log \ Gamma \ left ({\ frac {1} {4}} + {\ frac {it} {2}} \ right)} \ cdot \ pi ^ {- {\ frac {1} {4}}} \ cdot \ left ({\ frac {1} {4}} + t ^ {2} \ right) \ right] \ cdot \ left [e ^ {i \ operatorname {Im} \ log \ Gamma \ left ({\ frac {1} {4}} + {\ frac {it} {2}} \ right)} \ cdot \ pi ^ {- {\ frac {it} {2}}} \ cdot \ zeta \ left ({\ frac {1} {2}} + it \ right) \ right] \ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fab1f611425db9fabdfb9962d54721e398c04711)

























































