Holditch theorem

A chord (blue) is moved within a curve (black) so that a point on the chord (red) draws another curve.

The set of Holditch is a set of plane geometry , the first time in 1858 by Hamnet Holditch was formulated. It provides a formula for the area of a surface that is created when a chord is moved along a closed curve .

formulation

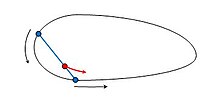
Let be a closed, convex curve. Let the chord of length be divided by the point into two segments, which have lengths and , and pass once. (So ​​that this is possible, it has to be sufficiently small.) The point describes a curve that does not overlap itself. Then the area between and has an area of . ${\displaystyle \Gamma }$ ${\displaystyle AB}$ ${\displaystyle a+b}$ ${\displaystyle C}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle \Gamma }$ ${\displaystyle a+b}$ ${\displaystyle C}$ ${\displaystyle \Gamma '}$ ${\displaystyle \Gamma }$ ${\displaystyle \Gamma '}$ ${\displaystyle \pi ab}$

The area is therefore independent of the shape and size of the curve and only depends on the length of the chord and the position of the point on it.

Holditch himself did not take into account a number of important points in the formulation, such as missing the condition that it is convex, that the tendon is short enough to be able to walk all the way around, and that it does not overlap itself . His proof also contains several unproven assumptions. ${\displaystyle \Gamma }$ ${\displaystyle \Gamma '}$

Special cases

Some special cases of Holditch's theorem can easily be proved by elementary geometry: If a circle is radius , then there is also a circle which has the same center as . Its radius is determined by drawing in a diameter of . This is divided by the point into two parts of length and , so that according to the chord rule applies. The area of ​​the ring between the two circles is in accordance with Holditch's statement. ${\displaystyle \Gamma }$ ${\displaystyle R}$ ${\displaystyle \Gamma '}$ ${\displaystyle \Gamma }$ ${\displaystyle r}$ ${\displaystyle \Gamma }$ ${\displaystyle C}$ ${\displaystyle R-r}$ ${\displaystyle R+r}$ ${\displaystyle ab=(R-r)(R+r)=R^{2}-r^{2}}$ ${\displaystyle \pi R^{2}-\pi r^{2}=\pi ab}$

If a rectangle , the sides of which are all longer than the chord, coincides with one part of the rectangle , only deviates in the corners and describes a quarter of an elliptical arc . The area between the curves therefore corresponds to the area of ​​an ellipse with the semi-axes and , so it is again . ${\displaystyle \Gamma }$ ${\displaystyle \Gamma '}$ ${\displaystyle \Gamma }$ ${\displaystyle \Gamma '}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle \pi ab}$

Generalizations

A generalization of Holditch's theorem comes from Arne Broman and at the same time provides a formal representation for the passage of the tendon.

Let be a closed, rectifiable plane curve, parameterized by for . Be continuous and of limited variation with , where is an integer. Let be points in the plane for and so that the segment has an angle of opposite a fixed reference straight line and is divided by the point into two partial segments of the lengths and . The curves they go through are and . Be and analog for and . Then: ${\displaystyle \Gamma _{A}}$ ${\displaystyle (x(t),y(t))=:A(t)}$ ${\displaystyle 0\leq t\leq 1}$ ${\displaystyle \theta :[0,1]\to \mathbb {R} }$ ${\displaystyle \theta (1)=\theta (0)+n\cdot 2\pi }$ ${\displaystyle n}$ ${\displaystyle t\in [0,1]}$ ${\displaystyle B(t)}$ ${\displaystyle C(t)}$ ${\displaystyle AB}$ ${\displaystyle \theta }$ ${\displaystyle C}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle \Gamma _{B}}$ ${\displaystyle \Gamma _{C}}$ ${\displaystyle I_{A}:=\int _{\Gamma _{A}}xdy}$ ${\displaystyle I_{B}}$ ${\displaystyle I_{C}}$

${\displaystyle I_{C}={\frac {b}{a+b}}I_{A}+{\frac {a}{a+b}}I_{B}-n\pi ab}$

Holditch's theorem results as a special case if and is. According to Green's theorem, the area between the curves is even , which is actually what it is according to the above formula . ${\displaystyle \Gamma _{A}=\Gamma _{B}}$ ${\displaystyle n=1}$ ${\displaystyle I_{A}-I_{C}}$ ${\displaystyle \pi ab}$

The proof of the theorem can be done by simple calculations with curve integrals .

It is probably not possible to generalize the theorem to higher dimensions.

Applications

Holditch's theorem and its generalizations can be applied to the study of kinematic chains , with their help it is possible to determine the space requirements of structures when the end points of moving rods are guided on certain paths.

swell

• Arne Broman: Holditch's Theorem. A fresh look at a long forgotten theorem. In: Mathematics Magazine. Vol. 54, No. 3, May 1981. pp. 99-108. ( JSTOR 2689793 )

Web links

• Eric W. Weisstein : Holditch's Theorem . In: MathWorld (English).