Takagi function

Approximation of the graph of the Takagi function on the unit interval.

Animation of the approximation of the graph of the Takagi function on the unit interval based on the nth partial sum for n = 0,1,2,3,4,5,10,50,100.

The Takagi function (also known as the Blancmange function ) is a real-valued function of a real variable. It is a continuous but not differentiable function over the entire domain of definition .

history

The function was originally given by the Japanese mathematician Takagi Teiji in 1903 as an example of a continuous and nowhere differentiable function. Karl Weierstrass and Bernard Bolzano had already found other examples of such functions in the 19th century . Initially, the function received little attention from Western mathematicians. In 1930 the Dutchman van der Waerden published a similar function with the base ten instead of two. Nine years later, the Norwegian mathematician Tambs-Lyche took up the Takagi function again as an example of a continuous and nowhere differentiable function accessible to beginning mathematics students. The function is also known as the Blancmange function due to the similarity of its graph to the sweet almond soup ( French : blanc-manger).

definition

The Takagi function is defined as

${\displaystyle T\colon [0,1]\to \mathbb {R} ,\;x\mapsto \sum _{n=0}^{\infty }{\frac {\phi (2^{n}x)}{2^{n}}}}$,

where is the distance from to the nearest whole number . ${\displaystyle \textstyle \phi (x):=\min _{k\in {\mathbb {Z} }}|x-k|}$ ${\displaystyle x}$

Takagi originally presented the function slightly differently. The range of definition can be periodically expanded to completely . ${\displaystyle \mathbb {R} }$

properties

Convergence and continuity

The Takagi function is well defined since the series converges for all of them . This can be shown, for example, with the Weierstrasse majorant criterion . See the sequence of functions with , for everyone . It applies to everyone that , there . In addition, according to convergence, the geometric series applies . So, according to Weierstrasse's majorant criterion, the series even converges evenly and absolutely . ${\displaystyle x\in [0,1]}$ ${\displaystyle \textstyle T(x)=\sum _{n=0}^{\infty }{\phi (2^{n}x) \over 2^{n}}}$ ${\displaystyle \textstyle (f_{n})_{n\in \mathbb {N} _{0}}}$ ${\displaystyle \textstyle f_{n}\colon [0,1]\to \mathbb {R} ,\;x\mapsto {\frac {\phi (2^{n}x)}{2^{n}}}}$ ${\displaystyle \textstyle n\in \mathbb {N} _{0}}$ ${\displaystyle \textstyle n\in \mathbb {N} _{0}}$ ${\displaystyle \textstyle \sup _{x\in [0,1]}f_{n}(x)\leq {\frac {1}{2^{n+1}}}=:M_{n}}$ ${\displaystyle \textstyle \phi (2^{n}x)\leq {\frac {1}{2}}}$ ${\displaystyle \textstyle \sum _{n=0}^{\infty }M_{n}={\frac {1}{2}}\sum _{n=0}^{\infty }\left({\frac {1}{2}}\right)^{n}={\frac {\frac {1}{2}}{1-{\frac {1}{2}}}}=1<\infty }$ ${\displaystyle \textstyle T(x)=\sum _{n=0}^{\infty }f_{n}(x)=\sum _{n=0}^{\infty }{\phi (2^{n}x) \over 2^{n}}}$

The Takagi function is continuous . Because the partial sums are continuous functions for all and, as shown above, converge uniformly to the Tagaki function. ${\displaystyle \textstyle \sum _{n=0}^{N}{\phi (2^{n}x) \over 2^{n}}}$ ${\displaystyle \textstyle N\in \mathbb {N} _{0}}$

Indistinguishability

The Takagi function is not differentiable at any point in its domain (in the sense of the topology induced by the ordinary amount on the real numbers ).

Proof (after Billingsley ): Be arbitrary. For everyone be and with , so that applies and . Be like above . Then the following applies for the difference quotient: ${\displaystyle x\in [0,1]}$ ${\displaystyle k\in \mathbb {N} }$ ${\displaystyle a_{k}:=2^{-k}s_{k}}$ ${\displaystyle b_{k}:=2^{-k}t_{k}}$ ${\displaystyle s_{k},t_{k}\in \mathbb {N} }$ ${\displaystyle a_{k}-b_{k}=2^{-k}}$ ${\displaystyle b_{k}\leq x<a_{k}}$ ${\displaystyle \textstyle f_{n}\colon [0,1]\to \mathbb {R} ,\;x\mapsto {\frac {\phi (2^{n}x)}{2^{n}}}}$

${\displaystyle {\frac {T(a_{k})-T(b_{k})}{a_{k}-b_{k}}}=\sum _{n=0}^{k-1}{\frac {f_{n}(a_{k})-f_{n}(b_{k})}{a_{k}-b_{k}}}=\sum _{n=0}^{k-1}f_{n}^{+}(x)}$,

where is the right derivative of at . The first equality is true because is for everyone . The second equality, however, follows, since the interval is linear with a slope . But because , according to the zero sequence criterion , the difference quotient for cannot converge. So it is not differentiable at this point . ${\displaystyle f_{n}^{+}(x)}$ ${\displaystyle f_{n}}$ ${\displaystyle x}$ ${\displaystyle f_{n}(a_{k})=f_{n}(b_{k})=0}$ ${\displaystyle n\geq k}$ ${\displaystyle f_{n}}$ ${\displaystyle [b_{k},a_{k}]}$ ${\displaystyle f_{n}^{+}(x)}$ ${\displaystyle f_{n}^{+}(x)\in \{-1,+1\}}$ ${\displaystyle k\to \infty }$ ${\displaystyle T}$ ${\displaystyle x}$

Graphic properties

The graph of the Takagi function can be approximated using the first partial sum of the series . The following graphic illustrates this for various values ​​of . In each step triangular waves with halving period length and height (in red) are added to the graph (which corresponds exactly to the next summand in the series). ${\displaystyle N\in \mathbb {N} _{0}}$ ${\displaystyle \textstyle T(x)=\sum _{n=0}^{\infty }{\phi (2^{n}x) \over 2^{n}}}$ ${\displaystyle N}$

${\displaystyle N=0}$	${\displaystyle N=1}$	${\displaystyle N=2}$	${\displaystyle N=3}$

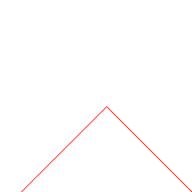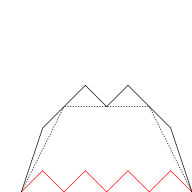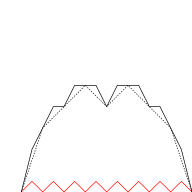
The Takagi function assumes its maximum of uncountably many points with a value of . Your graph is a fractal and has a Hausdorff dimension of one. ${\displaystyle \textstyle {\frac {2}{3}}}$

See also

• Weierstrass function

Individual evidence

1. ↑ ^{a b} Konrad Königsberger: Analysis 1 . 6th edition. Springer, Berlin 2004, ISBN 978-3-540-40371-5 , 9.11.
2. ^ Teiji Takagi: A Simple Example of the Continuous Function without Derivative . In: Phys.-Math. Soc. Japan . tape 1 , 1903, p. 176-177 .
3. ^ ^{A b c d e} Pieter C. Allaart and Kiko Kawamura: The Takagi Function: a Survey. In: Real Anal. Exchange 37 (2011/12), no.1, 1-54 . tape 37 , no. 1 , 2012, p. 1-54 .
4. ↑ Eric W. Weisstein: Blancmange Function. In: MathWorld-A Wolfram Web Resource. Retrieved July 26, 2018 .