Partial discharge
Partial discharge (abbreviated TE ) or pre-discharge is a term from high-voltage technology that primarily concerns the shape and properties of insulating materials . If strongly inhomogeneous field profiles occur in high-voltage insulation or along airways, the breakdown field strength typical of the material may be exceeded locally . In this state of imperfect electrical breakdown, the insulation between the electrodes is only partially bridged by discharges. Such partial discharges mainly occur when the insulation is exposed to alternating voltage .
Formation of partial discharges
Partial discharges arise in media with inhomogeneous field profiles through electron emission from free charge carriers, caused by external influences. The picture shows schematically the development of a partial discharge in a tip-plate electrode arrangement, caused by incident radiation. It shows an inhomogeneous electric field in which there are atoms. Radiation comes in from outside with the energy . This can for example be ultraviolet radiation or other ionizing radiation . If a photon with sufficient energy hits an atom to loosen an electron from its bond, a free electron is created ( photoelectric effect ). This in turn is drawn to the positively charged plate electrode due to the prevailing field, and on its way can release electrons from other atoms ( avalanche effect ). This creates a large number of free charge carriers that form a conductive channel in which an electrical discharge (movement of the charge carriers towards the electrode) takes place. Since this discharge does not extend over the entire distance between the electrodes, it is referred to as a partial discharge. Another cause of a partial discharge can be the "suction" of electrons from an electrode due to strong fields ( field emission ).
In technical applications, especially in high-voltage technology, attempts are made to prevent the formation of inhomogeneous field profiles, for example by means of field scattering electrodes and corona rings . However, damage to components can promote inhomogeneous field profiles and thus the development of partial discharges.
Categorization
The term partial discharge is an umbrella term under which the following partial discharge effects are summarized.
External partial discharges (corona)
External partial discharges are discharges on the surfaces of free metal electrodes into the surrounding air space. They occur primarily on sharp-edged parts where the field strength increases significantly. This phenomenon is generally known with the audible and visible corona discharges on high-voltage overhead lines. External pre-discharges can be avoided by the round design of all edges, as well as by field-controlling rings. Field-controlling rings are used, for example, on high-voltage cascades. The St. Elms fire also involves external partial discharges.
Internal partial discharges

All externally not visible discharge phenomena within insulating media are generally referred to as internal partial discharges. The insulating media can be solid, liquid or gaseous materials.
Discharges occur where inhomogeneities in the medium are under strong field influence, for example in the case of gas bubbles that are in an insulating liquid, such as oil, or in casting resin. These gas bubbles, consisting of air, carbon dioxide (e.g. in the case of the influence of moisture during the curing of polyurethane resin) or oil decomposition gases, have a lower dielectric constant than the surrounding oil, which increases the field strength. The insulating properties at the location of the gas bubble are disturbed by the locally lower dielectric strength, which is noticeable through partial discharges. Incorrect connection of built-in parts in components manufactured using cast resin or impregnation (switched-mode power supply transformers, high-voltage cascades) also lead to partial discharges. Further examples are non-encapsulated transformer windings made of enamelled copper wire in switched-mode power supply transformers and loosely wound film capacitors for AC voltage applications. Shielded cables are also affected if the braided shield or inner conductor is not completely in contact with the dielectric. Since this is hardly achievable, one makes do with conductive layers at the interfaces.
Due to the ultraviolet radiation and ionization, internal partial discharges lead in the long term to damage to the surrounding organic insulating material and must therefore be avoided.
Transformers (especially high-voltage transformers and switched-mode power supply transformers) are therefore often vacuum-soaked or cast under vacuum.
Sliding discharges
In the case of sliding discharges, the phenomenon of partial discharge occurs at the boundary layer of an insulating material along the field. In this case, the homogeneous course of the electrical field is disturbed and can lead to sliding discharges along the boundary layer. Dirt and moisture promote this phenomenon. However, when clean, many insulating materials have a lower dielectric strength along their surfaces than the air gap of the same length. Here, too, these sliding or pre-discharges lead to damage, especially in the case of organic insulating materials, to the occurrence of leakage currents and, as a result, to breakdown. Sliding discharges can be avoided by extending the boundary layer and protecting against moisture (ribs on insulators , impregnation). Another measure is the attachment of metal subdivisions of defined potentials (field control).
Importance and measurement technology

Partial discharges are generally undesirable; they lead to energy losses on overhead lines and to harmful effects caused by ionization on or in components. Partial discharge measurements are therefore carried out on electrical engineering components such as transformers , capacitors , high-voltage bushings, insulators , instrument transformers and optocouplers .
The focus here is on the safety aspect, since solid insulation, which can lead to partial discharges during operation, is not permanently reliable. In order to guarantee this long-term stability, the PD measurement proves that even if there is a partial discharge, it is safely below a limit value again above the highest operating voltage that occurs. In this way, the partial discharge extinction voltage (UTA) is determined, which must be above a limit value that was specified in the context of the insulation coordination with the customer in relation to the application. There are various standards for this in the area of, among others, the Association of Electrical, Electronic and Information Technologies (VDE) and the International Electrotechnical Commission (IEC 60270) .
The partial discharges are measured with typical measuring receivers in the range from about 100 kHz to a few MHz. The lower measurement threshold is also rare p by faults in shielded measuring stations under 1 C . In measuring stations, oscilloscopes represent the test voltage (mostly 50 Hz, but in the case of switched-mode power supply transformers in the range of their operating frequency) together with the high-frequency partial discharge pulses and, depending on their position relative to one another, allow further interpretations as to whether it is external or internal PD, for example. A typical PD measurement according to regulations includes the regulation of the operating voltage to the value of 1.8 times the rated voltage , which is held for a certain time. At this voltage there is no measurement, it only serves as an "excitation". The actual measurement takes place at 1.3 times the rated voltage.
An example of safety-relevant components are ignition transformers for controlling the power semiconductors in railway electric drives, which all undergo a 100% partial discharge measurement in the final test. Large transformers and other high-voltage components, for example in substations, are regularly checked with mobile PD measuring systems in order to be able to plan preventive maintenance and replacement measures.
Measurement of partial discharges
In order to be able to measure and assess PD impulses according to IEC 60270 (High-voltage test techniques - Partial discharge measurement), these must be decoupled from the test object and fed to a suitable evaluation system for signal conditioning, signal processing , visualization and data backup. PD measuring devices are available for this purpose, which usually allow single-channel PD measurements in partially predefined fixed frequency bands. These measuring systems are mainly optimized for test field use and do not allow sufficient flexibility to e.g. B. to be able to appropriately evade frequency-fixed interferers temporarily occurring under on-site conditions by varying the measurement frequency or measurement bandwidth. Sensitive PD measurements on site are usually not possible.
Additional methods are therefore in use, for example acoustic methods, the detection of ultraviolet radiation , the detection of decomposition products of the insulating materials or the reception of the radio waves generated by the PD in the UHF range.
Electric and magnetic processes
Conventional PD decoupling
According to IEC 60270 (High-voltage test techniques - Partial discharge measurement), partial discharges are measured at the end of the cable. The PD pulses are decoupled via a measuring impedance ( four-pole decoupling ), which converts the pulse-like recharging current of the coupling capacitor connected in parallel to the test object into a charge-equivalent voltage signal caused by the local insulation breakdown in the test object . This voltage signal reaches the PD measuring device via the cable .
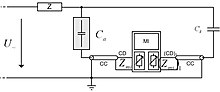
Measuring circles
Several types of interconnection of the device under test , coupling capacitor and measuring impedance ( , ) are possible. Figure 2 shows the measurement setup with a grounded coupling capacitor .
In this case the DUT is in series with the measurement impedance , which leads to a good measurement sensitivity for DUTs with a small capacitance value. In the event of a breakdown of the test object, the full test voltage is applied to the measurement impedance with this circuit , so that the downstream measurement technology must be protected against overvoltage.
Since an isolated installation or separation of the earth connection is not possible with most high-voltage test objects, the measuring impedance must be introduced into the earth branch of the coupling capacitor in this case. For this purpose, it must be set up isolated and the earth connection of the test object remains. Figure 3 shows this connection variant.
The sensitivity that can be achieved with both named variants of PD measurement is largely determined by the size of the available coupling capacitor and thus by the ratio of the capacitance to the test object . The measurable charge of a PD pulse is calculated from the apparent charge as follows:
Figure 4 illustrates the relationship graphically.
Due to their great length, cable systems represent an enormous capacitive load (e.g. 400 kV VPE diagonal Berlin: approx. 11.5 km, approx. 2.2 μF; London 400 kV VPE: 20 km, 4 , 4 μF; Augsburg 110 kV VPE: approx. 3.8 km, approx. 700 nF). With the commonly available capacitance values of on-site suitable coupling capacitors for the required voltage levels, this would inevitably result in a considerable reduction in the measurement sensitivity. A PD measurement with a coupling capacitor does not make sense. As an alternative, for single-phase PD measurements on cable systems, it is possible to use a neighboring phase (or both neighboring phases, cf.) as a coupling capacitor. At this point, the requirement for the coupling capacitor to be PD-free is given up in favor of a significantly increased measurement sensitivity. If PD signals occur, however, by comparing the measurement results of all three phases, it can be clearly clarified which of the phases is affected by PD.
Another variation in the simultaneous measurement of two phases of a cable system is the decoupling of PD signals via a bridge circuit (see Figure 5), which enables a high level of common mode rejection.
This measuring principle is based on the assumption that the measurable signals of occurring PD errors from the DUT do not correlate in time with pulses from the neighboring phase functioning as a coupling capacitor. In contrast, interference pulses (mainly corona interferers coupled into the cable ends of parallel live systems) run through both phases involved in the measurement and occur at the same time (and with the same polarity) at the measurement location. By using a ferrite transformer for PD decoupling, these common mode interferers can be effectively suppressed. This measuring method assumes that the test voltage source can provide sufficient power for several phases on site.
Measuring impedance
The measurement impedance is mostly set up as a passive analog bandpass filter . Low frequency components, primarily the area close to the test and operating frequency, are highly suppressed to protect the connected measurement technology . The PD pulses are decoupled in a broad undamped range (<1 MHz). Permanently integrated filters (band-stop filters) can also be installed in this decoupling area, which suppress, for example, narrow-band, frequency-fixed interferers such as amplitude-modulated radio transmitters. It must be ensured here that the reduction in the usable frequency spectrum consequently reduces the energy of the PD pulse that can be coupled out. In the case of mobile PD measurement systems, it can also be assumed that, due to regional differences in the terrestrial transmission frequencies, permanently implemented bandstop filters are not useful. Here the suppression of these interferers can be done by programmable filters on the software side of the PD measurement system, e.g. B. by adaptive filter algorithms.
Another purpose of bandpass filtering in the measurement impedance is a quasi-integration of the measurement signal in the time domain to determine the impulse charge. According to Fourier, the spectral energy of any current pulse is calculated according to:
As is well known, the current integral over time is the impulse charge we are looking for and is calculated as follows:
Mathematically, the spectral signal component for direct voltage (f = 0 Hz) corresponds to the charge value sought . However, since, as described above, frequencies in the range of the test voltage (and below) are suppressed during coupling, this frequency component is not available for further evaluation. Assuming that the course of the frequency spectrum is almost constant up to a characteristic cut-off frequency , a correct charge determination is possible by means of a bandpass measurement in the range of this constant amplitude of the frequency spectrum of a PD pulse above 0 Hz. If the current interference spectrum of the environment is known, the narrow-band bandpass measurement also enables the targeted selection of a frequency range for PD measurement that is largely free of frequency-fixed interferers.
Non-conventional field coupling
As already described in the previous chapter, the classic decoupling of PD pulses at the cable ends using a coupling capacitor and measuring impedance often does not lead to the required measuring sensitivities of a few pico coulombs . PD detection by means of field coupling is an alternative to this classic galvanic decoupling. With this method, suitable field sensors record the electrical and magnetic field components generated by PD pulses and convert them into measurable voltage signals.
Field sensors generally work in a frequency range above 1 MHz and are therefore not IEC-compliant. In addition, they are not considered to be calibratable in the classic sense (output signal in mV instead of pC). However, these sensors have already proven themselves through a large number of successful measurements under disturbed on-site conditions. Field sensors and their calibration will therefore be taken into account in upcoming standard adaptations, but not yet in the current revision of IEC 60060-3 for the standardization of on-site testing and measurement technology. In addition, it is common in testing operations for high-voltage cable systems that agreements between the customer and the testers supplement valid standards. The use of field sensors is already common today and in many cases the only sensible method for signal acquisition during PD measurements on extensive cable systems.
The area around the cable fittings is a useful installation location for field sensors. On the one hand, the field sensor can be implemented on site during the assembly of the fittings with little additional work. Field sensors can often be integrated into sets during their manufacture in the factory, so that no additional work steps are necessary on site. On the other hand, the sensor is placed with its mounting in close proximity to the set close to the potential TE void because the VPE - high voltage cable freedom TE is already in the cable plant to have been studied, so usually only components that are assembled on site, such as sleeves and terminations, come into question as PD defects.
Another positive effect of PD decoupling by means of field sensors is the interference-suppressing effect of the test item itself. Due to the large cable capacitance, the test item acts as a low-pass filter and thus attenuates external interference pulses in the relevant frequency range greater than 1 MHz to such an extent that they are released from the field sensors in the area of the Sockets can only be detected with a greatly reduced amplitude. The monitoring area of the field sensors can thus be limited to the vicinity of the sets.
Capacitive sensors
The electrical field component of a PD pulse is recorded by capacitive sensors. The sensor electrode can be implemented as a conductive strip in the form of a cylinder jacket around the cable core (CCS, Coaxial Cable Sensor, see Figure 6). The sensor electrode works together with the outer cable shield as a capacitance. A capacitive voltage divider is created from the cable and sensor, which enables pulse-like signals to be extracted from the power cable.
This type of capacitive sensor must be installed on site. As a result, the opened cable shield and the protective cable jacket must be restored after the sensor has been installed, and their proper condition must be verified. The measuring line, which leads the sensor potential for measurement from the cable to the outside, should also be mentioned as an additional weak point. This inevitably penetrates the cable jacket and must therefore be adequately protected against possible water ingress.
Capacitive field sensors that were implemented directly in the clothing during manufacture are more sophisticated in terms of design. The existing field-controlling deflectors can be used as capacitive sensor surfaces. The semiconducting and thus frequency-dependent character of the deflector material is used. While the deflector for the operating-frequency fields takes on the field-controlling function within the sleeve construction, high-frequency fields caused by PD can be tapped at this via a shunt resistor for measurement purposes.
Since in most cases only a single capacitive sensor is implemented per sleeve, it is not possible to precisely locate a PD error by evaluating the runtime within the sleeve. Fault location to the centimeter is only possible to a very limited extent, even with two sensors, due to the upper limit frequency of the sensor, which is limited to around 20 MHz.
In the frequency range of approx. 2 MHz to 20 MHz typical for capacitive sensors, high-frequency pulses are already so strongly attenuated as they propagate in the cable that the decrease in pulse amplitudes from the point of origin to the measurement location and the pulse deformation in general allow a clear differentiation of the pulse origin (see Fig Figure 7).
For example, corona disturbances can be clearly distinguished from TE from the socket. Independent of this, the high-precision recording of the absolute time enables the direction of the pulse propagation to be determined and thus also a reliable differentiation of the pulse origin.
For the reasons mentioned above, however, it is not possible to calibrate the capacitive sensor on site by feeding in a reference charge at the accessible cable end. The calibration pulse would have to run through the cable several 100 meters to the sensor in the first sleeve and would be strongly attenuated there. The calibration required for a quantitative PD evaluation must therefore take place in the laboratory using an additional sleeve with short cables. The sensitivity of the sensor is exclusively dependent on the cable-sleeve system (e.g. geometry, conductivity of the conductive layer). If there are two identical sensors on one socket, cross calibration is also conceivable. Here one of the sensors acts as a capacitor for feeding in the calibration signal, while the other sensor acts as a decoupling capacitor. According to the following equation, due to the symmetry of the sensors, half the value of the determined coupling attenuation corresponds to the attenuation value of an individual sensor:
Any signal losses that occur due to partial reflections within the sleeve construction must also be taken into account.
Directional coupling sensors
A directional coupler is a component known from antenna technology with which forward and reverse signals can be decoupled separately. The coupling behavior of directional coupler sensors is based on a superposition of inductive and capacitive coupling, the ratio of which can be adjusted. In an ideal directional coupler, both couplings are exactly the same size. Figure 8 shows the principle of constructive and destructive signal superposition.
A signal on line 1 (shown in Figure 8 by the directional current arrow , green) results in both a common-mode inductive coupling component ( , blue) and a push-pull capacitive coupling component ( , red) on line 2 , which are superimposed on the two measuring resistors and lead to the output signals described.
The directional coupler sensor is characterized by a clear indication of the direction of the pulse origin. A signal reaching the directional coupler sensor can be measured at the side of the directional coupler outputs (coupling path) facing the direction of origin (constructive superposition of the inductive and capacitive signal components), while ideally no output signal appears at the other output (blocking path) (destructive superposition). With ideal directional couplers, the signals in the blocking path are completely eliminated. In practice, real directional coupler sensors achieve a coupling ratio (signal ratio of blocking path to coupling path) of the order of 1:10. However, down to a signal ratio of 1: 2, a reliable statement about the direction of origin of the PD signals is usually unproblematic.
The directional coupler sensors are usually mounted inside the sleeve housing directly on the outer conductive layer of the cable, which is not influenced by this. Figure 9 shows a simple sensor for PD decoupling, which was subsequently attached to a cable sleeve.
By logically linking the four output signals of the two directional coupler sensors on a socket, the signals can be clearly classified as “coming from the left”, “coming from the right” and “TE from the socket”. For maximum decision-making certainty, which corresponds to a large directional ratio, the directional coupler sensor should be specially adjusted in its geometry for each cable, since the mechanical and electrical properties of the cable, e.g. B. the thickness of the insulation and the conductivity of the conductive layers are included in the directivity.
Inductive directional coupling sensors
Inductive coupling predominates in inductively tuned directional coupler sensors. In contrast to the directional coupler sensor considered up to now, the direction of pulse travel is determined by the polarity of the output signals of two sensors in the inductively tuned directional coupler. External interferences are coupled out with opposite polarity. Signals with the place of origin between the two sensors, e.g. B. TE from the socket, on the other hand, are decoupled with the same polarity and are thus clearly recognizable (Figure 10).
The functioning of the inductively tuned directional coupler sensors is derived from the basic principle of a directional coupler, in which the capacitive coupling is missing. The sensor and the inner conductor of the power cable forming a system of two coupled lines, a mutual inductance M K possess. The inductively tuned directional coupler sensor has only one output signal per sensor. The second output required for the directional coupler sensors is omitted because it contains redundant information. To monitor a socket, a sensor is installed on the left and right of the socket.
What is particularly advantageous about inductive directional coupler sensors is that, in contrast to “normal” directional coupler sensors, their geometry does not have to be specially adjusted for each cable and that the evaluation electronics only have to evaluate two signals on one sleeve. In addition, the required bandwidth of the evaluation electronics can be significantly reduced depending on the required sensitivity. At full bandwidth, however, the sensitivity is the same as with "normal" directional couplers. The decision-making certainty whether TE comes from the socket or from outside is not influenced. On the other hand, there is the justifiable disadvantage for practical use in many cases that the direction of origin can no longer be differentiated from external interference signals with the inductive directional coupler sensor.
Inductive sensors
Inductive sensors use the magnetic field component of a PD pulse and can be mounted outside over the sheath of the power cable. A shield must ensure that electrical fields do not interfere with the measurement signal. A common embodiment of an inductive sensor is the Rogowski coil , which is suitable for shielding electrical interference fields for decoupling PD pulses on power cables.
Rogowski coils are characterized by their large bandwidth and linear transmission behavior. When using line elements as shown in the adjacent figure, partial resonances may have to be expected when used at high cut-off frequencies (nanosecond range).
application
For useful applications of partial discharges see under ionizer and corona treatment .
With certain designs of nitrogen lasers , partial discharges are used to pre-ionize the discharge path so that the main discharge is more homogeneous.
In ignition devices for high-pressure gas discharge lamps and flash lamps , partial discharges support the ignition by ionizing the filling gas in the area of the mostly pointed electrodes with the help of a tip discharge .
literature
- Dieter König, Y. Narayana Rao: Partial discharges in energy technology equipment . VDE-Verlag GmbH, Berlin and Offenbach 1993, ISBN 3-8007-1764-6 .
Web links
Individual evidence
- ^ Crichton, Karlsson, Pedersen: Partial Discharges in Ellipsoidal and Spheroidal Voids, IEEE Transactions on Electrical Insulation, 1989, Vol 24, No. 2
- ↑ IEC 60270, High-voltage test techniques - Partial discharge measurement, Version 2000, 3rd Edition
- ↑ Plath, Heinrich, Rethmeier, Kalkner: Sensitive On-Site PD Measurements on Long Cable Systems, ISH03-13th International Symposium on High Voltage Engineering, Delft / Netherlands, 25-29th August 2003
- ^ Tian, Lewin, Davies, Swingler, Sutton, Hathaway: Comparison of On-line Partial Discharge Detection Methods for HV Cable Joints, IEEE Transactions on Dielectrics and Electrical Insulation, 2002, Vol. 9, No. 4th
- ↑ a b R.Plath, R. Heinrich, W. Weissenberg, K. Rethmeier, W. Kalkner: PD sensors for high-voltage XLPE cable fittings, ew-Elektrizitätswirtschaft issue 24/2002
- ↑ PCJM van der Wielen, Veen, Wouters, Steennis: Sensors for On-line PD Detection in MV Power Cables and their Locations in Substations ”, Proc. of the 7th International Conf. on Properties and Applications of Dielectric Materials, Nagoya, June 1-5, 2003
- ^ A b P. Wang, PL Lewin, SJ Sutton: Calibration of Capacitive Couplers for Online PD Detection in HV Cables, IEEE Electrical Insulation Magazine, 2005
- ↑ E DIN EN 60060-3 (VDE 0432-3): 2005-03, E DIN EN 60060-3 (VDE 0432-3): 2005-03: High-voltage testing technology - Part 3: Terms and requirements for on-site exams
- ↑ A.Küchler: High Voltage Engineering, 2nd Edition, Springer-Verlag, Berlin, 2005
- ^ Boggs, Braun, Stone: Attenuating Voltage Surges in Power Cable by Modifying the Semiconductive Shields, IEEE International Symposium on Electrical Insulation, Baltimore 1992
- ↑ R. Heinrich, K.Rethmeier, W.Kalkner, R.Plath, W.Weissenberg: Sensitive PD detection on high voltage XLPE cable lines using field coupling sensors, JiCable03 - 6th International Conference on Insulated Power Cables, 22-26 June 2003 , Paris-Versailles / France
- ↑ Henningsen, Polster, Fruth, Gross: Experience with an On-Line Monitoring System for 400 kV XLPE Cables, Proc. Of the 1996 IEEE Power Engineering Society Transmission and Distribution Conference, Sept. 1996, pp. 515-520
- ↑ Chen Min; K. Urano, A. Kato, Y. Sakaguchi, G. Okamoto, H. Ueno, K. Hirotu, A. Jinno, M. Okada, N. Yoshikawa: Study of partial discharge localization methods for EHV prefabricated joint, IEEE Power Engineering Society Summer Meeting, 2000
- ↑ DW Gross: On-site partial discharge diagnosis and monitoring on HV power cables, JiCable99 - 5th International Conference on Insulated Power Cables - June 20-24, 1999, Paris-Versailles / France
- ↑ Benzerouk, Patsch, Menzel: Identification of PD sources on the basis of waveform analysis, Hanau 2005
- ↑ Azcarraga, Garcia-Colon: Establishment of Ultra Wide Band Sensors Transfer Function for Qualitative PD Measurement, ISH05-14th International Symposium on High Voltage Engineering, Bejing / PRChina, 25-29th August 2005
- ^ Meinke, Friedrich-Wilhelm Gundlach , Lange, Locher: Taschenbuch der Hochfrequenztechnik, Vol. 1–3, Heidelberg 1986
- ↑ K.Rethmeier: Simulation and metrological verification of field sensors for location-selective PD measurement on high-voltage cable accessories, diploma thesis, TU-Berlin 1999
- ↑ Rethmeier, Kay - New decoupling methods and sensors for on-site partial discharge measurement on high-voltage cable systems , dissertation, TU-Berlin 2006
- ↑ D. Pommerenke, T. Strehl, W. Kalkner: Directional Coupler Sensor for Partial Discharge Recognition on High Voltage Cable Systems, ISH97 - 10th International Symposium on High Voltage Engineering, Montreal 1997
- ↑ R. Heinrich: Basic research on VHF / UHF sensors for on-site PD measurement on high-voltage cables with special attention to directional coupler technology, dissertation, TU-Berlin 2001
- ^ R. Heinrich, K. Rethmeier, W. Kalkner: Inductive directional couplers as new sensors for PD detection and localization on high voltage XLPE cable accessories, JiCable03 - 6th International Conference on Insulated Power Cables, 22-26 June 2003, Paris-Versailles / France
- ↑ Xin, Chengrong, Wang, Bin, Weijiang: Partial Discharge Measurement in XLPE Cable Joint by Using VHF Sensor, Proc. 2004 IEEE International Conf. on Solid Dielectrics, Toulouse, France, July 5-9, 2004
- ↑ W.Rogowski, W.Steinhaus: The measurement of magnetic power, Archives of Electrical Engineering, 1912
- ^ F. Kohlrausch: Practical Physics 2, BG Teubner, Stuttgart 1985
- ↑ L. Bergmann, C. Schaefer: Textbook of Experimentalphysik 2, Walter de Gruyter, Berlin 1987
- ↑ Schichler, Borsi, Gockenbach: Problems an New Solutions for Partial Discharge Measurement on High Voltage Cables under Noisy Conditions, IEEE Int. Symposium on Electrical Insulation, USA 1994
- ^ WF Ray, CR Hewson: High Performance Rogowski Current Transducers, IEEE - IAS Conf. Proc, Rome, September 2000
- ↑ H. Bellm, A. Küchler, J. Herold, A. Schwab: Rogowski coils and magnetic field sensors for measuring transient currents in the nanosecond range, Springer-Verlag 1985