Root diffusion process

This article or the following section is not adequately provided with supporting documents ( e.g. individual evidence ). Information without sufficient evidence could be removed soon. Please help Wikipedia by researching the information and including good evidence.

Three paths of root diffusion processes

The root diffusion process (the English term square root diffusion is also used in German-speaking countries ) is a stochastic process that is defined by a stochastic differential equation . Since this process class was first studied in 1951 by the Croatian- American mathematician William Feller , it has found numerous fields of application in various areas of financial mathematics .

Definition and parameters

Three independent processes with v0 = 1, theta = 0.6, sigma = 0.2, kappa = 20

Let real parameters and a Brownian motion be given. A stochastic process is called a root diffusion process with those parameters if it uses the stochastic differential equation ${\displaystyle \kappa \geq 0,\;\theta >0,\sigma }$ ${\displaystyle (W_{t}),\ t\geq 0}$ ${\displaystyle (X_{t}),\;t\geq 0}$

${\displaystyle dX_{t}=\kappa (\theta -X_{t})dt+\sigma {\sqrt {X_{t}}}dW_{t}}$

solves. In most cases, an initial condition is specified with, so that the above differential equation becomes a stochastic initial value problem . ${\displaystyle X_{0}=x}$

One reason for the popularity of this process is certainly that the modes of action of the individual parameters are easy to interpret (and can therefore be used as "adjusting screws" in modeling):

• ${\displaystyle \theta }$is the equilibrium level of the process ( mean reversion level ). If , the drift term is positive and "pulls" the process upwards, otherwise it is negative and tends downwards. So always drifts in anticipation . ${\displaystyle X_{0}<\theta }$ ${\displaystyle \kappa (\theta -X_{t})dt}$ ${\displaystyle X}$ ${\displaystyle X_{t}}$ ${\displaystyle \theta }$
• ${\displaystyle \kappa }$indicates the strength of this regulating function ( mean reversion speed ). For this is overridden and the course of depends only on the diffusion term . The larger , the more "rigid" is to bound. Theoretically, negative values ​​for would also be conceivable, but then the process would have completely different properties: if started above , it would diverge towards , otherwise it would soon be negative - and thus fall out of its own definition range. ${\displaystyle \kappa =0}$ ${\displaystyle X}$ ${\displaystyle {\sqrt {X_{t}}}dW_{t}}$ ${\displaystyle \kappa }$ ${\displaystyle X}$ ${\displaystyle \theta }$ ${\displaystyle \kappa }$ ${\displaystyle \theta }$ ${\displaystyle +\infty }$
• The parameter is the volatility of the process. It controls how much the Brownian motion is exposed to fluctuations. For large values ​​of will fluctuate very strongly over time, for converges exponentially to . ${\displaystyle \sigma }$ ${\displaystyle X}$ ${\displaystyle \sigma }$ ${\displaystyle X}$ ${\displaystyle \sigma =0}$ ${\displaystyle X}$ ${\displaystyle \theta }$

properties

theta = 1.4, otherwise the same values ​​as above

Although the above differential equation does not have a closed solution (i.e. it is not possible to express the resulting process as a function of and ), a lot can be said about the properties of the process: ${\displaystyle X}$ ${\displaystyle t}$ ${\displaystyle W}$

• For is never negative, i.e. H. it applies . If the stability condition also applies , it is almost certainly strictly positive. This is due to the fact that the diffusion term also tends towards zero and thus the positive drift "pulls" the process upwards again. ${\displaystyle \kappa \geq 0}$ ${\displaystyle X}$ ${\displaystyle \forall t\geq 0:\;P(X_{t}\geq 0)=1}$ ${\displaystyle 2\kappa \theta \geq \sigma ^{2}}$ ${\displaystyle X}$ ${\displaystyle X_{t}\to 0}$
• Was given a preceding value with , then has a non-central chi-squared distribution , in which the non-centrality parameter of depends. ${\displaystyle X_{u}}$ ${\displaystyle u<t}$ ${\displaystyle X_{t}}$ ${\displaystyle X_{u}}$
• In the long term, the distribution converges from regardless of the starting point to a gamma distribution with expected value and variance . If this distribution is chosen as the start distribution, it has the same distribution at all times. ${\displaystyle X_{t}}$ ${\displaystyle \theta }$ ${\displaystyle {\frac {\sigma ^{2}\theta }{2\kappa }}}$ ${\displaystyle X}$
• The root diffusion process is an affine process

application

Cox-Ingersoll-Ross model

here sigma = 0.4

In 1985, in their pioneering work A theory of the term structure of interest rates, the American mathematicians Cox, Ingersoll and Ross proposed the root diffusion process as a model for short-term interest rates . At the same time they presented new approaches for calculating transition probabilities of the process. Their interest rate model soon became one of the standard models on the market, so that the root diffusion process was soon nicknamed the CIR process .

Heston model for stochastic volatility

In 1993, Steven L. Heston gave the 'square-root diffusion' new popularity when he developed a complex capital market model by adding a stochastic volatility to the model of Black and Scholes , which the latter had assumed to be constant. This was simulated by a root diffusion and could thus for the first time be correlated with the stock market price via the Brownian movement : This made it possible to mathematically capture the natural phenomenon ( leverage ), according to which falling prices increase the excitement (volatility) in the markets. The Heston model is seen today as the most important extension to Black-Scholes and finally gave root diffusion a regular place in textbooks on stochastic processes.

Stochastic time shift

Same values ​​as above, but theta = 1 and kappa = 50 (note the scale)

Another possibility of using the CIR process to provide general Lévy processes (a much broader class than the process class examined by Heston) with stochastic volatility is based on an idea by Wolfgang Döblin ( Alfred Döblin's son ) from the 1930s : At the time, Döblin suggested controlling the volatility of a process by controlling the speed of the time in which the process runs. Many decades later it turned out that the root diffusion process is ideally suited to influencing this speed as an upstream "time machine". For example, if there is such a Lévy process and the process defined above, one obtains through a process with stochastic time. ${\displaystyle (L_{t}),\;t\geq 0}$ ${\displaystyle X}$ ${\displaystyle Y_{t}:=L_{X_{t}},t\geq 0}$ ${\displaystyle Y}$

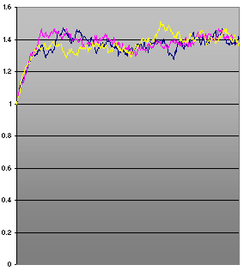
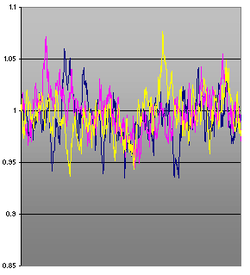
Simulation of the process

In practice there are two ways to simulate the CIR process, both of which have their advantages and disadvantages:

• One possibility is to use the known transition probability (non-central chi-square distribution) and to draw the next one (at any distance) directly for each given point. This method offers an exact (in the sense of: unambiguous) simulation of the process, but a normal and a gamma distributed random variable must be drawn for each step to determine the chi-square distributed update . The latter, however, is numerically complex to draw, which makes this technology appear unsuitable for Monte Carlo simulations , for example .
• The second option - not exact, but faster and suitable for finer grids - is the simulation using a simple Euler-Maruyama method (this is how the sample images for this article were created). It should be noted, however, that the Euler update can become negative in every step with a positive probability (which is not the case with the real process), which not only causes numerical problems.