Diameter: Difference between revisions

Content deleted Content added

Inline

Revision as of 00:04, 6 May 2024

Circle with
  circumference C

  diameter D

  radius R

  centre or origin O

In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere.

In more modern usage, the length $d$ of a diameter is also called the diameter. In this sense one speaks of the diameter rather than a diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius $r.$

d=2r\qquad {\text{or equivalently}}\qquad r={\frac {d}{2}}.

For a convex shape in the plane, the diameter is defined to be the largest distance that can be formed between two opposite parallel lines tangent to its boundary, and the width is often defined to be the smallest such distance. Both quantities can be calculated efficiently using rotating calipers.^[1] For a curve of constant width such as the Reuleaux triangle, the width and diameter are the same because all such pairs of parallel tangent lines have the same distance.

For an ellipse, the standard terminology is different. A diameter of an ellipse is any chord passing through the centre of the ellipse.^[2] For example, conjugate diameters have the property that a tangent line to the ellipse at the endpoint of one diameter is parallel to the conjugate diameter. The longest diameter is called the major axis.

The word "diameter" is derived from Ancient Greek: διάμετρος (diametros), "diameter of a circle", from διά (dia), "across, through" and μέτρον (metron), "measure".^[3] It is often abbreviated ${\text{DIA}},{\text{dia}},d,$ or $\varnothing .$

Generalizations

The definitions given above are only valid for circles, spheres and convex shapes. However, they are special cases of a more general definition that is valid for any kind of $n$ -dimensional (convex or non-convex) object, such as a hypercube or a set of scattered points. The diameter or metric diameter of a subset of a metric space is the least upper bound of the set of all distances between pairs of points in the subset. Explicitly, if $S$ is the subset and if $\rho$ is the metric, the diameter is

\operatorname {diam} (S)=\sup _{x,y\in S}\rho (x,y).

If the metric $\rho$ is viewed here as having codomain $\mathbb {R}$ (the set of all real numbers), this implies that the diameter of the empty set (the case $S=\varnothing$ ) equals $-\infty$ (negative infinity). Some authors prefer to treat the empty set as a special case, assigning it a diameter of $0,$ ^[4] which corresponds to taking the codomain of $d$ to be the set of nonnegative reals.

For any solid object or set of scattered points in $n$ -dimensional Euclidean space, the diameter of the object or set is the same as the diameter of its convex hull. In medical parlance concerning a lesion or in geology concerning a rock, the diameter of an object is the least upper bound of the set of all distances between pairs of points in the object.

In differential geometry, the diameter is an important global Riemannian invariant.

In planar geometry, a diameter of a conic section is typically defined as any chord which passes through the conic's centre; such diameters are not necessarily of uniform length, except in the case of the circle, which has eccentricity $e=0.$

Symbol

The symbol or variable for diameter, ⌀, is sometimes used in technical drawings or specifications as a prefix or suffix for a number (e.g. "⌀ 55 mm"), indicating that it represents diameter.^[5] Photographic filter thread sizes are often denoted in this way.^[6]

The symbol has a Unicode code point at U+2300 ⌀ DIAMETER SIGN, in the Miscellaneous Technical set, and should not be confused with several other Unicode characters that resemble it but have unrelated meanings.^[7] It has the compose sequence Composedi.^[8]

Diameter vs. radius

The diameter of a circle is exactly twice its radius. However, this is true only for a circle, and only in the Euclidean metric. Jung's theorem provides more general inequalities relating the diameter to the radius.

References

^ Toussaint, Godfried T. (1983). "Solving geometric problems with the rotating calipers" (PDF). Proc. MELECON '83. Mediterranean Electrotechnical Conference, 24-26 May 1983, Athens. IEEE. CiteSeerX 10.1.1.155.5671. (pdf pages in reversed order)
^ Bogomolny, Alexander. "Conjugate Diameters in Ellipse". www.cut-the-knot.org.
^ "diameter - Origin and meaning of diameter by Online Etymology Dictionary". www.etymonline.com.
^ "Re: diameter of an empty set". at.yorku.ca.
^ Puncochar, Daniel E. (1997). Interpretation of Geometric Dimensioning and Tolerancing. Industrial Press Inc. p. 5. ISBN 9780831130725.
^ Ciaglia, Joseph (2002). Introduction to Digital Photography. Prentice Hall. p. 9. ISBN 9780130321367. The filter diameter (in mm) usually follows the symbol ⌀
^ Korpela, Jukka K. (2006). Unicode Explained. O'Reilly Media, Inc. p. 171. ISBN 9780596101213.
^ Monniaux, David. "UTF-8 (Unicode) compose sequence". Retrieved 2018-07-13.

[1] Toussaint, Godfried T. (1983). "Solving geometric problems with the rotating calipers" (PDF). Proc. MELECON '83. Mediterranean Electrotechnical Conference, 24-26 May 1983, Athens. IEEE. CiteSeerX 10.1.1.155.5671. (pdf pages in reversed order)

[2] Bogomolny, Alexander. "Conjugate Diameters in Ellipse". www.cut-the-knot.org.

[3] "diameter - Origin and meaning of diameter by Online Etymology Dictionary". www.etymonline.com.

[4] "Re: diameter of an empty set". at.yorku.ca.

[5] Puncochar, Daniel E. (1997). Interpretation of Geometric Dimensioning and Tolerancing. Industrial Press Inc. p. 5. ISBN 9780831130725.

[6] Ciaglia, Joseph (2002). Introduction to Digital Photography. Prentice Hall. p. 9. ISBN 9780130321367. The filter diameter (in mm) usually follows the symbol ⌀

[7] Korpela, Jukka K. (2006). Unicode Explained. O'Reilly Media, Inc. p. 171. ISBN 9780596101213.

[8] Monniaux, David. "UTF-8 (Unicode) compose sequence". Retrieved 2018-07-13.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

@@ Line 1: / Line 1: @@
+{{Short description|Straight line segment that passes through the centre of a circle}}
-{{Otheruses}}
+{{Other uses}}
+{{use British English|date=March 2021}}<!-- so centre not center -->
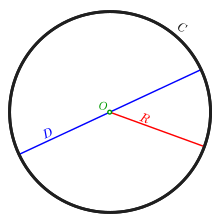
-[[File:Circle-withsegments.svg|thumb|200px|right|Circle with [[circumference]] (C) in black, diameter (D) in cyan, radius (R) in red, and centre or origin (O) in magenta.]]
+[[File:Circle-withsegments.svg|thumb|right|Circle with {{legend-line|black solid 3px|[[circumference]] ''C''}}
+{{legend-line|blue solid 2px|diameter ''D''}}
+{{legend-line|red solid 2px|radius ''R''}}
+{{legend-line|green solid 2px|centre or origin ''O''}}]]
 {{General geometry}}
-In [[geometry]], a '''diameter''' of a [[circle]] is any straight [[line segment]] that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest [[chord (geometry)|chord]] of the circle. Both definitions are also valid for the diameter of a [[sphere]].
+In [[geometry]], a '''diameter''' of a [[circle]] is any straight [[line segment]] that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest [[Chord (geometry)|chord]] of the circle. Both definitions are also valid for the diameter of a [[sphere]].
-In more modern usage, the length of a diameter is also called the diameter. In this sense one speaks of ''the'' diameter rather than ''a'' diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the [[radius]] '''r'''.
+In more modern usage, the length <math>d</math> of a diameter is also called the diameter. In this sense one speaks of {{em|the}} diameter rather than {{em|a}} diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the [[radius]] <math>r.</math>
-: <math>d = 2r \quad \Rightarrow \quad r = \frac{d}{2}.</math>
+:<math>d = 2r \qquad\text{or equivalently}\qquad r = \frac{d}{2}.</math>
-For a [[convex set|convex shape]] in the plane, the diameter is defined to be the largest distance that can be formed between two opposite [[parallel lines]] tangent to its boundary, and the ''width'' is often defined to be the smallest such distance. Both quantities can be calculated efficiently using [[rotating calipers]].<ref>{{cite journal
+For a [[convex set|convex]] shape in the [[plane (geometry)|plane]], the diameter is defined to be the largest distance that can be formed between two opposite [[parallel lines]] [[tangent]] to its boundary, and the {{em|width}} is often defined to be the smallest such distance. Both quantities can be calculated efficiently using [[rotating calipers]].<ref>{{cite conference |last=Toussaint |first=Godfried T. |contribution=Solving geometric problems with the rotating calipers |title=Proc. MELECON '83 |conference=Mediterranean Electrotechnical Conference, 24-26 May 1983, Athens |year=1983 |publisher=IEEE |citeseerx=10.1.1.155.5671 |contribution-url=http://www-cgrl.cs.mcgill.ca/~godfried/publications/calipers.pdf }} (pdf pages in reversed order)</ref> For a [[curve of constant width]] such as the [[Reuleaux triangle]], the width and diameter are the same because all such pairs of parallel tangent lines have the same distance.
-| author = Toussaint, Godfried T.
-| title = Solving geometric problems with the rotating calipers
-| publisher=Proc. MELECON '83, Athens
-|year = 1983
-| citeseerx = 10.1.1.155.5671
-}}</ref> For a [[curve of constant width]] such as the [[Reuleaux triangle]], the width and diameter are the same because all such pairs of parallel tangent lines have the same distance.
 {{Anchor|Ellipse}}
-For an [[ellipse]], the standard terminology is different. A diameter of an ellipse is any [[Chord (geometry)|chord]] passing through the center of the ellipse.<ref>{{cite web|url=http://www.cut-the-knot.org/Curriculum/Geometry/ConjugateDiameters.shtml|title=Conjugate Diameters in Ellipse|first=Alexander|last=Bogomolny|website=www.cut-the-knot.org}}</ref> For example, [[conjugate diameters]] have the property that a tangent line to the ellipse at the endpoint of one of them is parallel to the other one. The longest diameter is called the [[major axis]].
+For an [[ellipse]], the standard terminology is different. A diameter of an ellipse is any [[chord (geometry)|chord]] passing through the centre of the ellipse.<ref>{{cite web|url=http://www.cut-the-knot.org/Curriculum/Geometry/ConjugateDiameters.shtml|title=Conjugate Diameters in Ellipse|first=Alexander|last=Bogomolny|website=www.cut-the-knot.org}}</ref> For example, [[conjugate diameters]] have the property that a tangent line to the ellipse at the endpoint of one diameter is parallel to the conjugate diameter. The longest diameter is called the [[major axis]].
-The word "diameter" is derived from [[Ancient Greek|Greek]] διάμετρος (''diametros''), "diameter of a circle", from διά (''dia''), "across, through" and μέτρον (''metron''), "measure".<ref>{{cite web|url=http://www.etymonline.com/index.php?term=diameter|title=diameter - Origin and meaning of diameter by Online Etymology Dictionary|website=www.etymonline.com}}</ref> It is often abbreviated '''DIA''', '''dia''', '''d''', or '''⌀'''.
+The word "diameter" is derived from {{lang-grc|διάμετρος}} ({{transl|grc|diametros}}), "diameter of a circle", from {{lang|grc|διά}} ({{transl|grc|dia}}), "across, through" and {{lang|grc|μέτρον}} ({{transl|grc|metron}}), "measure".<ref>{{cite web|url=http://www.etymonline.com/index.php?term=diameter|title=diameter - Origin and meaning of diameter by Online Etymology Dictionary|website=www.etymonline.com}}</ref> It is often abbreviated <math>\text{DIA}, \text{dia}, d,</math> or <math>\varnothing.</math>
-==Generalizations==
+== Generalizations ==
+{{See also|Metric space#Diameter of a metric space}}
-The definitions given above are only valid for circles, spheres and convex shapes. However, they are special cases of a more general definition that is valid for any kind of ''n''-dimensional convex or non-convex object, such as a [[hypercube]] or a set of scattered points. The '''diameter''' of a [[subset]] of a [[metric space]] is the [[supremum|least upper bound]] of the set of all distances between pairs of points in the subset. So, if ''A'' is the subset, the diameter is
-:[[supremum|sup]] { d(''x'', ''y'') | ''x'', ''y'' ∈ ''A'' } .
-If the [[distance function]] d is viewed here as having [[codomain]] '''R''' (the set of all [[real number]]s), this implies that the diameter of the [[empty set]] (the case {{nowrap|1=''A'' = ∅}}) equals −∞ ([[negative infinity]]). Some authors prefer to treat the empty set as a special case, assigning it a diameter equal to 0,<ref>{{cite web|url=http://at.yorku.ca/cgi-bin/bbqa?forum=ask_a_topologist_2004;task=show_msg;msg=0860.0002|title=Re: diameter of an empty set|website=at.yorku.ca}}</ref> which corresponds to taking the codomain of d to be the set of nonnegative reals.
+The definitions given above are only valid for circles, spheres and convex shapes. However, they are special cases of a more general definition that is valid for any kind of <math>n</math>-dimensional (convex or non-convex) object, such as a [[hypercube]] or a [[set (mathematics)|set]] of scattered points. The {{em|{{visible anchor|diameter|Diameter of a set|Diameter of a subset}}}} or {{em|{{visible anchor|metric diameter|Metric diameter of a set|Metric diameter of a subset}}}} of a [[subset]] of a [[metric space]] is the [[supremum|least upper bound]] of the set of all distances between pairs of points in the subset. Explicitly, if <math>S</math> is the subset and if <math>\rho</math> is the [[Metric (mathematics)|metric]], the diameter is
-For any solid object or set of scattered points in n-dimensional [[Euclidean space]], the diameter of the object or set is the same as the diameter of its [[convex hull]]. In medical [[Idiom#Parlance|parlance]] concerning a lesion or in geology concerning a rock, the diameter of an object is the supremum of the set of all distances between pairs of points in the object.
+<math display="block">\operatorname{diam}(S) = \sup_{x, y \in S} \rho(x, y).</math>
+If the metric <math>\rho</math> is viewed here as having [[codomain]] <math>\R</math> (the set of all [[real number]]s), this implies that the diameter of the [[empty set]] (the case <math>S = \varnothing</math>) equals <math>- \infty</math> ([[negative infinity]]). Some authors prefer to treat the empty set as a special case, assigning it a diameter of <math>0,</math><ref>{{cite web|url=http://at.yorku.ca/cgi-bin/bbqa?forum=ask_a_topologist_2004;task=show_msg;msg=0860.0002|title=Re: diameter of an empty set|website=at.yorku.ca}}</ref> which corresponds to taking the codomain of <math>d</math> to be the set of nonnegative reals.
-In [[differential geometry]], the diameter is an important global [[Riemannian geometry|Riemannian]] [[invariant (mathematics)|invariant]].
+For any solid object or set of scattered points in <math>n</math>-dimensional [[Euclidean space]], the diameter of the object or set is the same as the diameter of its [[convex hull]]. In medical [[Idiom#Parlance|parlance]] concerning a lesion or in geology concerning a rock, the diameter of an object is the least upper bound of the set of all distances between pairs of points in the object.
-In plane geometry, a diameter of a [[conic section]] is typically defined as any chord which passes through the conic's centre; such diameters are not necessarily of uniform length, except in the case of the circle, which has [[eccentricity (mathematics)|eccentricity]]&nbsp;''e''&nbsp;=&nbsp;0.
+In [[differential geometry]], the diameter is an important global [[Riemannian geometry|Riemannian]] [[Invariant (mathematics)|invariant]].
-==Symbol==
-[[Image:Technical Drawing Hole 01.svg|thumb|122px|Sign ⌀ in a technical drawing]]
-[[Image:Sign diameter.png|thumb|150px|Sign {{unichar|2205|EMPTY SET|ulink=Mathematical Operators}} from an [[AutoCAD]] drawing in dim.[[shapefile|shx]] font with an angle 16°. This font does not contain {{unichar|2300|DIAMETER SIGN|ulink=Miscellaneous Technical}}.]]
-{{distinguish|text=the Scandinavian letter "[[Ø]]", the [[empty set]] symbol {{italics correction|"}}''∅''", the [[slashed zero]], or the greek letter [[phi]] (Φ)}}
+In [[planar geometry]], a diameter of a [[conic section]] is typically defined as any chord which passes through the [[center (geometry)#Projective conics|conic's centre]]; such diameters are not necessarily of uniform length, except in the case of the circle, which has [[Eccentricity (mathematics)|eccentricity]] <math>e = 0.</math>
-The [[symbol]] or [[variable (mathematics)|variable]] for diameter, {{char|⌀}}, is sometimes used in technical drawings or specifications as a prefix or suffix for a number (e.g. "⌀ 55 mm", indicating that it represents diameter. For example, photographic [[filter thread]] sizes are often denoted in this way.
+== Symbol ==
-In [[German (language)|German]], the diameter symbol (German ''[[:de:Durchmesserzeichen|Durchmesserzeichen]]'') is also used as an [[average]] symbol (''Durchschnittszeichen'').
+{{redirect|⌀}}
+[[Image:Technical Drawing Hole 01.svg|thumb|122px|Sign ⌀ in a technical drawing]]
+[[File:Hama UV Filter 1.jpg|thumb|A [[photographic filter]] marked as having a 58mm thread diameter]]
+The [[symbol]] or [[Variable (mathematics)|variable]] for diameter, {{char|⌀}}, is sometimes used in technical drawings or specifications as a prefix or suffix for a number (e.g. "⌀ 55 mm"), indicating that it represents diameter.<ref>{{cite book|title=Interpretation of Geometric Dimensioning and Tolerancing|first=Daniel E.|last=Puncochar|publisher=Industrial Press Inc.|year=1997|isbn=9780831130725|page=5|url=https://books.google.com/books?id=76la9qNmt24C&pg=PA5}}</ref> Photographic [[filter thread]] sizes are often denoted in this way.<ref>{{cite book|title=Introduction to Digital Photography|first=Joseph|last=Ciaglia|publisher=Prentice Hall|year=2002|isbn=9780130321367|page=9|quote=The filter diameter (in mm) usually follows the symbol ⌀}}</ref>
+The symbol has a [[Unicode]] [[code point]] at {{unichar|2300|Diameter sign|html=}}, in the [[Miscellaneous Technical]] set, and should not be confused with several other Unicode characters that resemble it but have unrelated meanings.<ref>{{cite book|title=Unicode Explained|first=Jukka K.|last=Korpela|publisher=O'Reilly Media, Inc.|year=2006|isbn=9780596101213|page=171|url=https://books.google.com/books?id=lxndiWaFMvMC&pg=PA171}}</ref> It has the [[compose sequence]] {{key press|[[Compose key|Compose]]|d|i|chain=}}.<ref>{{cite web |url=http://cgit.freedesktop.org/xorg/lib/libX11/plain/nls/en_US.UTF-8/Compose.pre |title=UTF-8 (Unicode) compose sequence |last=Monniaux |first=David |access-date=2018-07-13}}</ref>
-===Similar symbols===
-It is [[Homoglyph|similar in size and design]] to {{char|ø}}, the [[Ø|Latin small letter o with stroke]]. The diameter symbol ⌀ is distinct from the [[empty set]] symbol {{char|∅}}, from an ([[italic script|italic]]) uppercase [[Phi (letter)|phi]] {{char|''Φ''}}, and from the Nordic vowel {{char|Ø}} ([[Ø|Latin capital letter O with stroke]]).<ref>{{citation|title=Unicode Explained|first=Jukka K.|last=Korpela|publisher=[[O'Reilly Media, Inc.]]|year=2006|isbn=978-0-596-10121-3|pages=23–24|url=https://books.google.com/books?id=lxndiWaFMvMC&pg=PA23}}.</ref> See also [[slashed zero]].
+== Diameter vs. radius ==
-===Encodings===
+The diameter of a circle is exactly twice its radius. However, this is true only for a circle, and only in the [[Euclidean distance|Euclidean metric]]. [[Jung's theorem]] provides more general inequalities relating the diameter to the radius.
-The symbol has a [[Unicode]] [[code point]] at {{unichar|2300|Diameter sign|html=}}, in the [[Miscellaneous Technical]] set. On an [[Apple, Inc.|Apple]] [[Macintosh]], the diameter symbol can be entered via the character palette (this is opened by pressing {{key press|Opt}}{{key press|Cmd}}{{key press|T}} in most applications), where it can be found in the Technical Symbols category. In Unix/Linux/ChromeOS systems, it is generated using {{keypress|ctrl|shift|u}}{{nbsp}}{{keypress|2|3|0|0|space|chain=}} It can be obtained in UNIX-like operating systems using a [[Compose key]] by pressing, in sequence, {{key press|[[Compose key|Compose]]}}{{key press|d}}{{key press|i}}<ref>{{cite web |url=http://cgit.freedesktop.org/xorg/lib/libX11/plain/nls/en_US.UTF-8/Compose.pre |title=UTF-8 (Unicode) compose sequence |last=Monniaux |first=David |access-date=2018-07-13}}</ref>
+== See also ==
-The character will sometimes not display correctly, however, since many [[Typeface|font]]s do not include it. In many situations the letter ø (the Latin small letter o with stroke) is an [[typographic approximation|acceptable substitute]], which in Unicode is {{unichar|00F8|html=}}. and on a Macintosh by pressing {{key press|Opt}} {{key press|O}} (the letter [[o]], not the number [[0 (number)|0]]). In Unix/Linux/ChromeOS systems, it is generated using {{keypress|ctrl|shift|u}}{{nbsp}}{{keypress|F|8|space|chain=}} or {{keypress|Compose|o|/|chain=}}. [[AutoCAD]] uses {{unichar|2205|EMPTY SET|ulink=Mathematical Operators}} available as a shortcut string {{Kbd|%%c}}.
+{{Div col|colwidth=30em}}
+* {{annotated link|Angular diameter}}
-In [[Microsoft Word]] the diameter symbol can be acquired by typing 2300 and then pressing Alt+X.
+* [[Caliper]], [[Micrometer (device)|micrometer]], tools for measuring diameters
+* {{annotated link|Conjugate diameters}}
-In [[LaTeX]] the diameter symbol can be obtained with the command <code>\diameter</code> from the wasysym package.
+* {{annotated link|Diameter (group theory)}}, a concept in [[group theory]]
-==See also==
-{{Div col|colwidth=20em}}
-* [[Angular diameter]]
-* [[Caliper]], [[micrometer]], tools for measuring diameters
-* [[Conjugate diameters]]
-* [[Diameter (group theory)]], a concept in [[group theory]]
 * [[Eratosthenes]], who calculated the diameter of the [[Earth]] around 240 BC.
-* [[Distance (graph theory)|Graph or network diameter]]
+* {{annotated link|Distance (graph theory)|Graph or network diameter}}
-* [[Hydraulic diameter]]
+* {{annotated link|Hydraulic diameter}}
-* [[List of gear nomenclature#Inside diameter|Inside diameter]]
+* {{annotated link|List of gear nomenclature#Inside diameter|Inside diameter}}* {{annotated link|Semidiameter}}
+* {{annotated link|Sauter mean diameter}}
-* [[Jung's theorem]], an inequality relating the diameter to the radius of the [[circumradius|smallest enclosing ball]]
+* {{annotated link|Tangent lines to circles}}
-* [[Semidiameter]]
-* [[Sauter mean diameter]]
-* [[Tangent lines to circles]]
 * The [[Screw thread#Diameters|diameters]] of a screwthread
-* [[Ø (disambiguation)]]
 {{div col end}}
-==References==
+== References ==
-{{Reflist}}
+{{reflist|group=note}}
+{{reflist}}
 {{Wiktionary|diameter}}

v t e Common punctuation and other typographical symbols
space , comma : colon ; semicolon ‐ hyphen ’ ' apostrophe ′ ″ ‴ prime . full stop
& ampersand @ at sign ^ caret / slash \ backslash … ellipsis * asterisk ⁂ asterism * * * dinkus
- hyphen-minus ‒ – — dash ⹀ ⸗ double hyphen
? question mark ! exclamation mark ‽ interrobang ¡ ¿ inverted ! and ? ⸮ irony punctuation
# number sign № numero sign º ª ordinal indicator % percent sign ‰ per mille ‱ basis point ° degree symbol ⌀ diameter sign
+ − plus and minus signs × multiplication sign ÷ division sign ~ tilde ± plus–minus sign ∓ minus-plus sign ^ caret
_ underscore ⁀ tie \| ¦ ‖ vertical bar • bullet · interpunct
© copyright symbol © copyleft ℗ sound recording copyright ® registered trademark ^SM service mark symbol ^TM trademark symbol
‘ ’ “ ” ' ' " " quotation mark ‹ › « » guillemet ( ) [ ] { } ⟨ ⟩ bracket ” ditto mark
† ‡ dagger ❧ fleuron (hedera, aldus) ☞ manicule ◊ ⌑ lozenge ¶ ⸿ pilcrow (paragraph mark) § section mark
Version of this table as a sortable list Currency symbols Diacritics (accents) Logic symbols Math symbols Whitespace Chinese punctuation Hebrew punctuation Japanese punctuation Korean punctuation