Limited growth

In mathematics, limited growth ( limited growth ) is a growth that is limited by a natural limit (also called capacity (limit) or saturation (limit / value) ). Growth can both up (limited shrinkage) and downwards limited to be.

properties

Model description

In the classic growth model of limited growth, the rate of change or proportional to the saturation deficit (also called residual stock or saturation deficit). The saturation deficit itself decreases exponentially . This remainder indicates the shortfall until the limit is reached. The stock in turn results from the difference between the saturation limit and the saturation deficit. ${\displaystyle B_{n+1}-B_{n}}$ ${\displaystyle B'(t)}$ ${\displaystyle S-B(t)}$

Essential terms and notation

• ${\displaystyle t}$denotes time .
• ${\displaystyle B}$ be the size of the population under consideration.
• ${\displaystyle B\left(0\right)={{B}_{0}}}$identifies the initial balance ( initial condition ) at the point in time . ${\displaystyle t=0}$
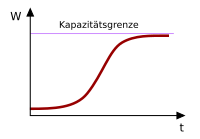
• ${\displaystyle S}$denotes the natural limit which, as a limit value for the size of the population, cannot (theoretically) be exceeded. It forms the asymptote of the growth function and prevents the stock from growing to infinity as with linear and exponential growth .
• ${\displaystyle k}$ be the growth constant.
• ${\displaystyle B'}$indicates the growth rate or the growth rate .

Differential equation

Differential equations (DGL) serve to describe the continuous ( steady ) growth model.

The DGL for limited growth is: ${\displaystyle {B}'\left(t\right)={\frac {\operatorname {d} B}{\operatorname {d} t}}=k\left(S-B\left(t\right)\right)}$

This is a linear inhomogeneous differential equation with constant coefficients and can be solved using the " variable separation " method.

Explicit representation (growth function)

The special solution of the DGL forms the explicit representation and thus at the same time the growth function .

The functional equation for a limited growth is: The growth is degressive . The rate of growth decreases over time. ${\displaystyle B\left(t\right)=S-(S-{{B}_{0}}){{\operatorname {e} }^{-kt}}}$

For an upwardly restricted growth with , the graph of the function rises strictly monotonically and describes a right-hand curve. ${\displaystyle S>{{B}_{0}}}$

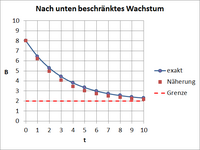
For a downwardly restricted growth with the graph of the function falls strictly monotonically and describes a left curve. ${\displaystyle S<{{B}_{0}}}$

For the special case of the growth function has the form: . ${\displaystyle S=0}$ ${\displaystyle B\left(t\right)=S-(S-{{B}_{0}}){{\operatorname {e} }^{-kt}}=0-(0{{\operatorname {e} }^{-kt}}-{{B}_{0}}{{\operatorname {e} }^{-kt}})=(0-0{{\operatorname {e} }^{-kt}})+{{B}_{0}}{{\operatorname {e} }^{-kt}}={{B}_{0}}{{\operatorname {e} }^{-kt}}}$

Here the limit coincides with the x-axis ( abscissa ). This corresponds to the classic case of an exponential decrease .

Recursive representation

To describe the discrete model as a recursive representation derived from differences are consequences .

Exact discretization

Be it . ${\displaystyle B_{n}=S-(S-B_{0})\mathrm {e} ^{-k\Delta t\cdot n}}$

Then the recurrence formula is: , ${\displaystyle B_{n+1}=B_{n}\mathrm {e} ^{-k\Delta t}+S\left(1-\mathrm {e} ^{-k\Delta t}\right)}$

where represents an equidistant sequence of points in time and means the corresponding stock sizes. ${\displaystyle \Delta t}$ ${\displaystyle t_{n}=t_{0},t_{1},t_{2},\dotsc }$ ${\displaystyle B_{n}=B_{0},B_{1},B_{2},\dotsc }$

Approximate discretization

The following approximation results from using the explicit Euler method : ${\displaystyle B_{n+1}=B_{n}+k\Delta t\left(S-B_{n}\right)}$

With ${\displaystyle B_{n}=B_{0}(1-k\Delta t)^{n}-S(1-k\Delta t)^{n}+S}$

Comparison between the exact and approximate representation

The comparison of the coefficients of the exact and approximate formulas shows that the two representations are not identical. By series expansion of the exponential function :

${\displaystyle \mathrm {e} ^{-k\Delta t}=1+{\frac {-k\Delta t}{1!}}+{\frac {(-k\Delta t)^{2}}{2!}}+\dotsb }$

it turns out, however, that both representations agree except for terms higher than 1st order.

Limited logistical growth

→ Main article : Logistic function  and population dynamics

In addition to the classic model, growth that can be described by a logistic function is also limited upwards. Here the rate of change is proportional to the product of stock and saturation deficiency . ${\displaystyle \,B'(t)}$ ${\displaystyle B(t)\cdot (S-B(t))}$

See also : Logistic growth

Examples

Growth limited to the top

Warming up a cold drink

If the temperature of a cold drink is below the ambient temperature, the drink is heated up to the ambient temperature, which forms the upper limit.

Sale of cellular connections at a fixed location

If all residents of the place have a mobile phone connection, the upper limit has been reached.

Taking medication

At the beginning of the intake, an active ingredient level builds up, which describes the upper limit with continuous medication.

Spread of a population in a limited area

A population e.g. B. Fish does not keep growing, but due to limited resources such as food, oxygen, space etc. there is a natural limit.

Downward growth restricted

Cooling off a hot drink

If the temperature of a hot beverage is above the ambient temperature, the beverage cools down to the ambient temperature, which forms the lower limit.

literature

• Joachim Engel: Application-Oriented Mathematics: From Data to Function. Pp. 152-154, Springer Verlag, Heidelberg 2010, ISBN 978-3-540-89086-7 .
• Hermann Haarmann, Hans Wolpers: Mathematics to obtain the general university entrance qualification, non-technical subjects. Pp. 273-274, 2nd edition. Merkur Verlag, Rinteln 2012, ISBN 978-3-8120-0062-8 .
• Harro Heuser: Ordinary Differential Equations: Introduction to Teaching and Use. Pp. 25-27, 70-72, Teubner Verlag, Wiesbaden, 5th edition 2006, ISBN 978-3-519-42227-3 .
• Klaus Schilling: Analysis: Qualification Phase. Pp. 207-218, EINS Verlag, Cologne 2012, ISBN 978-3-427-06660-6 .
• Walter Seifritz: Growth, Feedback and Chaos: An Introduction to the World of Nonlinearity and Chaos. Hanser Verlag, Munich 1987, ISBN 3-446-15105-2 .

Web links

• To the wiki: Limited growth
• Task examples with solutions (Abitur tasks Baden-Württemberg) ( Memento from December 23, 2012 in the Internet Archive )