Population dynamics
Population dynamics is the change in size, but also in the spatial distribution of biological populations in shorter or longer periods of time. Research into population dynamics in single or multiple coupled populations is a prominent subject in biology , especially ecology and theoretical biology . The population dynamics of species are determined by multifactorial interactions both within the population and with its animate and inanimate environment. This applies to short periods as well as very long periods.
Synecological aspects
Natural, but also most artificial systems, consist of several types, between which there are various interactions:
Boundary conditions of population growth
A distinction is made between two groups of factors that limit the density of a population:
Density-independent factors
They are independent of the number of individuals that populate a biotope .
- Weather and climatic conditions : The climatic events, which change over the day and week and vary slightly from year to year, with factors such as temperature, amount of precipitation, wind, solar radiation, etc.
- Disasters : Unpredictable events such as volcanic eruptions , devastating storms , floods , which can lead to the death of part of the population or the whole population (local extinction).
- Unspecific predators : enemies whose prey spectrum normally includes other living beings, and whose own population size is therefore independent of the prey they accidentally hunt.
- Inter-species (interspecific competition) competition : The population developments of different animal species in the same biotope with similar demands on food, territories and other resources can be more or less independent of one another if they occupy different ecological niches .
- Non-infectious diseases: In contrast to infectious diseases , which spread more easily in a denser population, non-infectious diseases are statistically occurring random events whose relative frequency does not increase with increasing density.
- Pesticides : The use of pesticides (in agriculture ) leads to the death of part of the population or even the entire population of certain species against which the pesticide is used, depending on the amount and intensity of the chemical substances used .
- Behavioral factors: reactions of prey animals and / or predators to environmental stimuli with trophic cascades
Density-dependent factors
The strength of their effects depends on the current population density.
- Intraspecific competition : The competition between individuals in a population for resources such as food , habitat, etc. This depends on the species-specific needs. Individuals of some animal species need large territories , while others live together in social associations (e.g. herds or states ) in a smaller space.
- Social stress (crowding factor): The coexistence of animals causes stress through encounters and aggression. The greater the density, the greater the stress, until behavioral changes, sterility or even death occur in some animal species.
- Predators: Animals that serve as prey for predators also have an impact on their population density. If the number of prey animals increases, the predators can raise correspondingly more young, which in turn increase the enemy pressure on the prey. (See predator-prey relationship )
- Contagious diseases ( infectious diseases ): Wherever individuals live in great confinement, there is also an increasing risk that an infectious disease will spread rapidly through the transmission of the pathogen and thus become an epidemic .
- Parasites: When there is a high population density, like infectious diseases, they can spread faster.
Basic forms of population dynamics
One-species models
One form of density-dependent growth is described by the logistic equation .
Logistic equation and influencing factors
Influencing factors are
- the birth rate
- the death rate
- the limiting capacity factor
- the reproductive self-restraint
In nature, the capacity limit is influenced by the following factors:
- density-independent factors, e.g. B.
- climate
- density-dependent factors, e.g. B.
- Resources like food, space
- Hiding places
- Crowd factor (social stress)
- emigration
- intraspecific competition - intraspecific competition
See also: Gompertz 'refined form of the logistic model and the mathematical derivation of the logistic function .
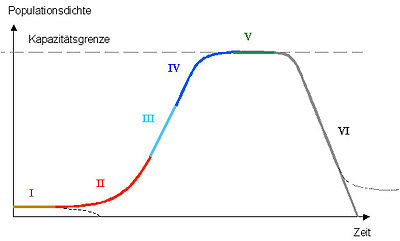
Typical phases of population development
Note: Not all phases have to occur in a real population. In the graphic, the downward branch in phase I shows, for example, that the population can die in phase I. The turn to the right in Phase VI indicates that population decline does not have to lead to extinction.
Phase I: lag phase ( to slow down), start-up phase, zero growth at a low level
The population size is far from the capacity limit. The birth rate is roughly equal to the death rate. There is no shortage of resources, density-dependent factors practically play no role, there is no competition. The birth rate is low, because with this low population density, intra-species encounters are random. The density-dependent mortality from predators only plays a minor role, as there are enough hiding places in the habitat for the few individuals. Infectious diseases also have little effect due to the rare intra-species encounters.
- Founder population: Small populations arise through the emigration of part of the population (example lemmings) or through disasters. If a small population colonizes a new habitat, some time can pass before the new food sources are optimally used by the population by changing the nutritional conditions.
- Substrate adaptation: In the case of microorganisms that can utilize different substrates, it usually takes some time (minutes to hours) for them to adapt to changed substrate offerings (for example, switching from anaerobic to aerobic metabolism in yeast cells). Hardly any growth can be observed during this transition phase. This applies in general if the capacity limit increases significantly due to improved living conditions.
Fluctuations in population density (oscillations) can, for example, be genetic, fluctuations are random. If the population falls below a certain density, the population can become extinct. When a certain value is exceeded, the population can enter the exponential phase.
Phase II to IV: phase of positive growth
The birth rate is higher than the mortality rate.
- Phase II: exponential growth (log phase). At first there is exponential growth, as the birth rate increases faster than the mortality rate. The resources are so abundant that intra-species competition does not matter. The predator population is initially so small or there are so many hiding spots that the mortality rate remains low. With very favorable living conditions, the exponential population growth can lead to a mass increase . However, as the population increases, so does the death rate.
- Phase III: linear growth. If the birth rate and death rate increase at the same rate, the population increases linearly.
- Phase IV: retarded growth. As the capacity limit increases, intra-species and possibly inter-species competition play an increasingly important role, so that the rise in the birth rate is slowed down and the death rate continues to rise. As the prey density increases, so does the population density of the predators, or the predators increasingly specialize in this prey. Further growth will be slowed down.

Phase V: stationary phase
The high birth rate is offset by a high density-dependent mortality rate (intra-species competition, stress, epidemics, etc.). There is maximum occupation of the habitat, the resources are used optimally without exhausting them (see load-bearing capacity of habitats ). The population density fluctuates around the value K , the capacity limit. Influences independent of density (e.g. seasons) lead to an oscillating or (in the case of unfavorable habitats with strongly fluctuating environmental influences) a fluctuating course. The larger a population, the more stable this stationary phase is. An overhang increases the death rate and / or lowers the birth rate in the short term. It can be reduced by emigration (example: lemmings ).
Phase VI: withering away
The birth rate is now lower than the death rate. With small populations, random fluctuations can lead to extinction. A lowering of the capacity limit, for example through environmental changes or the immigration of new predators, can bring about a new equilibrium at a lower level.
Multi-species models
A relatively simple case arises from interactions between two species that are in a predator-prey relationship . This case is classically described by the Lotka-Volterra rules .
More complex relationships result from the interaction of several species. There are approaches to describe and simulate such relationships with the help of mathematical models .
Population as a system
In the following, a mathematical modeling is to be developed based on considerations of system theory . It is first assumed that the resources for the population are unlimited. In contrast to some references, the birthrate and mortality rate are viewed as internal control variables . A change in population, for example due to birth, is therefore not perceived as a result of an influx from outside. (This would be more the case with immigration). Interactions with the environment in the form of immigration or emigration are also not taken into account.
- The birth rate is the positive control variable: the higher the birth rate, the larger the population.
- The death rate is the negative control variable: the higher the death rate, the smaller the population.
In general, such systems are represented by partial differential equations such as B. the Fisher equation . Special cases of this equation are dealt with below.
Population as an isolated system with no reaction
Influence of the birth rate
Only the influence of the birth rate on the rate of change of the population size N is considered:
(1)
This results (through integration ) under the condition that the birth rate is constant ( ) for the population size at any point in time t with the output variable N ( t = 0) = N 0 :
(2)
This results in positive linear growth , the speed of which depends only on the birth rate: the higher the birth rate, the faster the growth.
This system can be used as a model for insect states ( bees , ants , termites ) or other animal populations ( wolf packs ) in which only one female gives birth, but neglecting the death rate. However, it should not be forgotten that modeling leads to continuous growth, which in nature takes place in discrete steps. The birth rate is also likely to be constant only temporarily under ideal conditions.
Influence of the death rate
The mortality rate is:
(3)
with = c 2 = const. > 0.
(4)
This results in negative linear growth.
The extinction time, i.e. the time when the population became extinct, can also be calculated.
There is no equivalent for this in nature, since the death rate always depends on the population size. A regular removal of animals, for example from a herd of cattle for slaughter, would already correspond to the change in an open system.
Influence of birth and death rates
If the birth and death rates are taken into account at the same time, the change in the population over time results from:
(5)
Insertion of equations (2) and (4) and subsequent integration give:
(6)
Although the growth is still linear, whether the population increases, decreases or stagnates depends on the size of the birth and death rate:
- c 1 > c 2 : positive growth
- c 1 <c 2 : negative growth with
- c 1 = c 2 : zero growth ( stagnation )
Population as an isolated system with retroactive effects
In nature, birth and death rates depend on population density and the capacity of the ecosystem.
Independent birth rate and dependent death rate
In the following, the birth rate should continue to be independent of the population size, while the death rate depends on the population density: (The greater the population density , the greater the death rate). From this proportionality , with the help of the proportionality factor c 2 = const. > 0 the equation:
(7)
For the rate of change of the population size due to the death rate alone we get:
(8th)
This results from integration:
(9)
The inclusion of the constant birth rate independent of the population density gives:
(10)
Integration results in the equation
(11)
This system can change into a state of equilibrium different from N 0 . Equilibrium prevails when exactly as many are born as also die again, if so , or even if the rate of change is the population size .
From equation (10) the following results for the population size in equilibrium (equilibrium):
(12)
When the system is in equilibrium from the beginning and therefore in a stationary state. Despite growth through birth and loss through death, the population density does not change; there is zero growth. Otherwise the state of equilibrium is only reached (mathematically) with . The point in time from which one can practically speak of equilibrium could be calculated by stipulating that a minimal difference in comparison to N (for example 0.01%) is already regarded as an equilibrium situation.
Half-life of the equilibrium curve:
(13)
Based on the enzyme kinetics , a time could be calculated which corresponds to the Michaelis constant. t ½ N eq would be the point in time at which the population has reached half the equilibrium size:
(14)
Birth and death rates depend on population size
If all females in populations contribute to the birth rate, the birth rate also depends on the population density:
(15)
(The greater the population density, the greater the birth rate.) From this proportionality, with the help of the proportionality factor c 1 = const. > 0 the following equation:
(16)
For the rate of change of the population size due to the birth rate we get:
(17)
This results from integration:
(18)
This results in the rate of change in population size, taking into account the birth and death rate:
(19)
This results from integration:
(20)
Case distinctions:
- c 1 = c 2 : zero growth (stationary) at N 0
- c 1 > c 2 : positive exponential growth (accelerated increase)
- c 1 < c 2 : negative exponential growth (delayed decrease)
This system does not have an equilibrium state different from N 0 .
In a real population, however, the birth and death rate depend not only on the population density, but also on the distance between the population and the capacity limit , which is the maximum possible population size in the system: the closer a population is to the capacity limit (i.e. the smaller the Difference K - N ), the lower the birth rate and the higher the death rate.
These relationships are described in a simplified manner by the model of logistic growth (Verhulst):
Mathematical modeling
Basic equation (after Pierre-François Verhulst ):
(21)
Integration results in:
(22)
Case distinction:
- N < K : N ( t ) ≈ e rt , exponential (positively accelerated) growth when the population size is still very far away from the capacity limit.
- N = K : N ( t ) = K, zero growth (stagnation) when the population size equals the capacity limit.
- N > K : negative growth when the population density is above the capacity limit.
The model agrees quite well with the observations for organisms that multiply by dividing into two ( bacteria , yeasts and other eukaryotic unicellular organisms ) and higher organisms that have a low rate of reproduction per generation and whose generations overlap.
Are not described fluctuations and oscillations of the population density around the capacity limit and reduce the population near full capacity.
An extension of the formula of logistic growth to include time delays also results in periodic fluctuations in the model:
(23)
- = Delay in reproduction, e.g. gestation period
- = Response time delay of the population, for example when the capacity limit is exceeded
Models for interacting populations
Predator prey system
Predator-prey system according to the Lotka-Volterra equation :
(24.1)
(24.2)
N ( t ): number of prey animals at time t
P ( t ): number of predators at time t ,
a , b , c , d > 0: coefficients
Competitive model
(25.1)
(25.2)
r ( i ): linear birth rates
K ( i ): capacities, limited by resources
b (12), b (21): competitive effects from N 2 to N 1 , or from N 1 to N 2
Mutualism
(26.1)
(26.2)
Fluctuating population sizes
While the theoretical models contribute to the interpretation of actually observed fluctuations, they cannot always explain these fluctuations unequivocally. More or less regular fluctuations are also known as oscillations .
Examples of fluctuations:
- The best-known example is the lemmings with a turnover rate of 3 to 5 years, but a clear explanation is still pending.
- For the arctic fox in Scandinavia, a fluctuation rate of its population size of 3, elsewhere from 7 to 11 and in still others from 22 to 25 years is given; here the predator-prey system has to be applied twice: to him as predator and on him as prey.
- Fluctuations are also very clearly perceived in European wild animal populations, especially with wild boars . In the Hochtaunus district , the years 2000 to 2003 were considered to be very rich in wild boar, 2004 and 2005 as very poor in wild boar and again in 2008 as extraordinarily rich in wild boar. The local press provides extensive information about wild boar damage in one year and lack of wild boar meat in the other. The predator-prey system may apply here , with humans playing the role of predator , but other factors also play important roles, including swine fever and increased hunt due to swine fever, which reduced the transmission rate .
literature
- Josef Hofbauer , Karl Sigmund : Evolution theory and dynamic systems. Mathematical Aspects of Selection . Parey Verlag, Berlin, Hamburg 1984, ISBN 978-3-489-61834-8 .
- James D. Murray : Mathematical Biology, Volume I (3rd edition), Springer-Verlag , 2002
See also
Individual evidence
- ↑ Paws without claws? Ecological effects of large carnivores in anthropogenic landscapes [1]
- ↑ Literature review, section 2.1.5 Population dynamics, emigration behavior and population structure (p. 9)
- ↑ Lydia Bauer: Wild boar and deer in the districts ... since 1950: Shooting and population development, possible influencing factors, wild boar damage in agriculture Diploma thesis, Vienna 2006 (PDF; 7.4 MB)









































![{\ displaystyle {\ frac {\ mathrm {d} N_ {1}} {\ mathrm {d} t}} = r_ {1} N_ {1} \ left [1 - {\ frac {N_ {1}} { K_ {1}}} - b_ {12} {\ frac {N_ {2}} {K_ {1}}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3c207220d5c803d648f962f598e5eb851dff1de)
![{\ displaystyle {\ frac {\ mathrm {d} N_ {2}} {\ mathrm {d} t}} = r_ {2} N_ {2} \ left [1 - {\ frac {N_ {2}} { K_ {2}}} - b_ {21} {\ frac {N_ {1}} {K_ {2}}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5aa49220a4d59b619caa459fdb11c7a9804c2a7)
![{\ displaystyle {\ frac {\ mathrm {d} N_ {1}} {\ mathrm {d} t}} = r_ {1} N_ {1} \ left [1 - {\ frac {N_ {1}} { K_ {1}}} + b_ {12} {\ frac {N_ {2}} {K_ {1}}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ec8cceb23cd80e1df205966a210e328b45ba55c)
![{\ displaystyle {\ frac {\ mathrm {d} N_ {2}} {\ mathrm {d} t}} = r_ {2} N_ {2} \ left [1 - {\ frac {N_ {2}} { K_ {2}}} + b_ {21} {\ frac {N_ {1}} {K_ {2}}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc80e98efc48238eb64f19de15eef74d8f1b2788)