Block encryption
A block cipher (also block cipher or in English block cipher called) is a deterministic encryption method comprising a plaintext block, d. H. A plaintext section of fixed length is mapped to a ciphertext or ciphertext block of fixed (usually the same) length. This mapping is influenced by a key . If you know this, you can calculate the plain text from the ciphertext, with about the same effort as for the encryption. Without knowing the key, however, this is much more difficult and generally impractical.
In contrast to a stream cipher , a block cipher can only encode a block of the given length, whereby the block length is typically 64 bits to 256 bits. Longer texts are filled up to a multiple of the block length and divided into blocks, and an operating mode is selected which defines how the block cipher is to be applied to it.
Block ciphers are also used as building blocks for the construction of further cryptographic procedures, e.g. B. cryptographic hash functions are used.
conditions
A block cipher is supposed to withstand many attack scenarios. If, for example, an attacker has any number of pairs of plain text and ciphertext blocks generated with the same key, he should still not be able to determine the key or to decipher another ciphertext generated with this key in any other way . This should still apply even if the attacker can freely choose the plaintext blocks, i.e. can find out for each block constructed by him which is the ciphertext block belonging to the given key. Even if the attacker can freely choose a plain text or ciphertext block, it should be impossible for him to find out the key.
It is assumed that the attacker knows the internal structure of the encryption. The protection of the data should not depend on the secrecy of the procedure, but only on the secrecy of the key ( Kerckhoffs' principle ).
Neither the block size nor the key length can be too small. A block size of 64 bit, which is common with older block ciphers, is already borderline. If there are too few possible block values (here ), then a code book attack is possible. An attacker collects as many pairs of plain text and ciphertext blocks as possible for a particular key, and if one of these ciphertext blocks appears in any message (and the key has not been changed in the meantime), he also knows the plaintext block. On the other hand, if the key is too small, it is practical to try out all possible keys to find the right one. Modern methods use at least 128 bits as block and key length.
history
Lucifer is considered to be the first block cipher that can be used for civil purposes, it was developed by IBM in 1971 on the basis of Horst Feistel's cryptographic work. A revised version of Lucifer was adopted by the National Bureau of Standards (NBS) of the USA (from which the National Institute of Standards and Technology, NIST emerged in 1988) and declared a DES (Data Encryption Standard) after changes by the NBS itself and the NSA were made on the algorithm. The DES was presented to the public in 1976 and found widespread use. The block size of the DES is 64 bits and the key length is 56 bits.
As early as the end of the 1990s, DES could be broken by brute force attacks due to its small key length (see EFF DES Cracker ). It was therefore replaced by the AES (Advanced Encryption Standard) in 2001 after a five-year tender phase. The AES selection process is viewed by many cryptographers worldwide as exemplary because of its open design. The AES algorithm was developed by Joan Daemen and Vincent Rijmen under the name Rijndael. The block size is 128 bits and the key length is 128, 192 or 256 bits, selectable by the user.
Mathematical description
A block cipher is a function
- ,
which maps a plain text block to a ciphertext block , with the key as a parameter. The encryption function must be injective for every possible key , since then and there is a decryption function that calculates the plaintext for every ciphertext:
- .
This is equivalent to the statement that the decryption function is left-inverse to the encryption function.
Most often , and the encryption and decryption functions are then for each key from S bijective . Today, it also almost exclusively used Bitblockchiffren that on blocks with b bits work: . The block size is usually 64 or 128 bits, but larger values also occur (e.g. threefish ; up to 1024 bits).
A block cipher is called involutorial if encryption and decryption are identical, i.e. if:
- .
A bijective mapping from to is a permutation of elements. There is consequently an extremely large number ( ) of different mappings (see faculty ).
Using the key of a block cipher, exactly one of the possible bijective images is selected. Since the key length of typical block ciphers is far less than bits, only a small part of all possible images is covered by the totality of all keys. With a block size of only 8 bits, a 1684-bit key would be necessary to implement all permutations.
Design principles
There are two goals for the internal processing of the block data : Through confusion , the connection between secret and plain text should be made as complex and opaque as possible. Diffusion is intended to distribute the information at one point in the plaintext block over the entire ciphertext block; in the end, each bit of the ciphertext block should depend on each bit of the plaintext block and the key. If something is changed in these, each ciphertext bit should change with a probability of 1/2, without a recognizable system. There should be no possibility of obtaining any information about the plaintext or the key from a ciphertext.
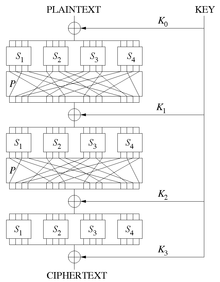
All modern block ciphers such as AES or DES are designed as iterated block ciphers. This means that the input is processed in several successive rounds that are structured in the same way (round function).
The difficulty in developing an encryption is to find a reversible transformation which meets the cryptographic requirements (confusion and diffusion) and which can be implemented and carried out efficiently with little effort. That is why you usually do not try to find a complex function that encrypts the text in a single step, but restrict yourself to a relatively simple round function. Only when they are used multiple times does a sufficiently complex encryption function result. The round function causes both confusion and diffusion, which effectively interlocks with each other during encryption. Sufficient rounds are run through to completely mix the data block several times, usually around 8 to 64 rounds. The round function is also set up in such a way that the diffusion properties between encryption and decryption do not differ significantly, so that there is also good diffusion during decryption.
The successive rounds should not work exactly the same as the process otherwise the so-called slide-attack (Engl. Slide attack ) would be vulnerable. This is why several different round keys are usually calculated from the user key, and in each round a different one is linked to the data block, either as a second entry in the round function:
- ,
or between applications of the round function, e.g. B. by bitwise XOR operation :
with lap number . This includes the round function, the plain text, the user key and the key classification function that provides the individual round keys. Cyclically repeating round keys should be avoided, as this would also enable a slide attack.
In addition, it is unfavorable if a section of the round keys only depends on a limited amount of data in the user key, for example in that the round keys used during the first half of the encryption only depend on one half of the user key and the remaining round keys only on the second half of the user key. The procedure would then be vulnerable to the meet-in-the-middle attack .
Feistel cipher
Feistel cipher, also known as Feistel network, is a general structure with which block ciphers can be implemented. Horst Feistel , who worked on the cipher Lucifer at IBM in 1970, is considered to be the inventor. A block of plain text is divided into two parts and processed in several rounds. In each round a block part is entered into the round function together with a round key and its output is linked to the other block part. Feistel networks allow decryption without having to calculate the inverse of the round function. Many ciphers, for example DES , Twofish and Blowfish , are structured as Feistel networks.
Lai Massey cipher
Here, similar to the Feistel network, a round function is used in such a way that its inverse does not have to be calculated for decryption. The data block is split in half . In each round you connect both halves with each other, enter the result in the round function and then connect their output with each of the block halves:
- .
This is done in such a way that is and you get the same input again when you repeat the operation . This makes it easy to reverse the round. The easiest way to do this is to use the bitwise XOR for and . Another possibility is to use for the subtraction , and for the encryption the addition and for the decryption the subtraction (or vice versa), each modulo , where the word length is in bits.
So that the successive rounds do not cancel each other out during encryption, the data block must be modified with another operation between the rounds. For this purpose, the bits of one half of the block are often permuted (e.g. by bit rotation ).
Examples of Lai-Massey ciphers are IDEA and IDEA NXT
Substitution-Permutation Network
The rounds of a substitution-permutation network are divided into three parts: First, the round key is linked to the data block. Then an S-Box is applied to the data block, which is divided into parts of bits that are substituted for themselves. Then the bits of the data block are permuted so that the output of an S-box is distributed over several S-boxes and finally over the entire data block in the next round. Often this permutation is replaced by a more complex operation, such as B. Serpent and AES to accelerate diffusion. In the last round, the permutation is superfluous, instead it is linked again with a round key.
These three steps have to be inverted for decryption. The S-Box must be bijective and the inverse S-Box must be used for decryption.
primitive
The individual operations in the round function (so-called cryptographic primitives) are often selected from those that can be carried out quickly by most microprocessors with a single machine command, so that the encryption can be easily and efficiently programmed in software:
- Addition , subtraction and multiplication of integers modulo , wherein the width of a data word in bits is
- bitwise Boolean operations: AND, OR, XOR, NOT
- Bit rotation
- Bit shift
With bit rotation and shifting, the shifting width can be constant, key-dependent (e.g. CAST ) or data-dependent ( RC5 , RC6 , MARS ).
Many modern block ciphers are so-called ARX ciphers, such as Threefish. This means that they are only made up of addition, rotation with constant width and XOR. This makes them easy to implement and efficient, although many rounds are usually necessary for sufficient strength of the encryption.
S-boxes are less efficient to implement in software, but they are also strong sources of confusion and therefore very effective cryptographically, because you can (largely) freely determine how the input bits are mapped from an S-box to the output bits. S-boxes can be constant (DES, AES, CAST) or key-dependent ( Blowfish ).
With regard to the implementation in hardware, the permutation of bits is also used in many ciphers (abundant, e.g. with DES), which can be easily implemented here, you just have to connect each bit line to the correct input of the subsequent gate . With software implementation, on the other hand, general bit permutations are awkward; the data word has to be broken down into individual bits, shifted and reassembled. Most of the time, this is easiest to represent as an S-Box that z. B. 8 bits are always replaced by a whole word that contains the entered bits in the correct positions, after which these words are combined by bitwise OR. A substitution with subsequent bit permutation can be combined into one operation.
Cryptographic modes of operation
A cryptographic operating mode defines how the encryption of several plaintext blocks is carried out by defining the type of encryption algorithm used on the data stream. The susceptibility to errors and security varies depending on the requirements of the application. The international standard ISO 10116 defines four different operating modes for block-oriented encryption algorithms:
- Electronic Code Book (ECB) : Each block is encrypted separately.
- Cipher Block Chaining (CBC) : Each block is XORed with the previous ciphertext block before it is encrypted.
- Cipher Feedback (CFB) : A ciphertext block is created by XORing the plaintext block with the previously encrypted ciphertext block.
- Output Feedback (OFB) : The block cipher is used like a stream cipher in that an initialization vector is repeatedly encrypted in order to link the next plain text block with it via XOR.
There is also Counter Mode (CTR) , in which a nonce is encrypted together with the number of a block. The result is XOR-linked with this block in the manner of stream encryption.
Some newer block ciphers, such as B. Threefish , accept an additional input, the so-called tweak , which influences the mapping of the plain text to the ciphertext . In English they are called tweakable block ciphers ; a German translation has not yet spread. If the tweak is changed, the permutation of the block values changes, just like if the key is changed. While the latter is time-consuming due to the complex key classification of many ciphers (an extreme example is Blowfish ), the tweak can be changed very easily and quickly.
This makes further operating modes possible. So you can modify ECB in such a way that each block is encrypted with a different tweak (but the same key). The tweak does not have to be kept secret. B. simply use the sequential number of the block. As a result, the same plain text blocks are no longer mapped to the same ciphertext blocks.
Well-known block ciphers
Some well-known block ciphers are:
- Camellia
- RC2
- Data Encryption Standard (DES)
- Triple DES (3DES)
- Advanced Encryption Standard (AES)
- International Data Encryption Algorithm (IDEA)
- FEAL
- RC5
- RC6
- Serpent
- Blowfish
- Twofish
- Skipjack
- CAST
- MARS
- Tiny Encryption Algorithm (TEA)
- Extended Tiny Encryption Algorithm (XTEA)
- SEED
Web links
- Klaus Pommerening: Bit block encryption . (PDF; 1.0 MB) Department of Mathematics at Johannes Gutenberg University
- Stefan Labitzke, Sven Kampfhenkel: Security aspects in software technology . (PDF; 1.7 MB), Faculty IV Computer Science at TU Berlin
Individual evidence
- ↑ Alex Biryukov and David Wagner on slide attacks (PDF)
- ↑ Bruce Schneier: Applied Cryptography. Protocols, Algorithms and Source Code in C . 2nd Edition. John Wiley & Sons, New York 1996, ISBN 0-471-11709-9 , pp. 206-208 .