
Curve
C (with locally variable curvature) and its circle of curvature to point
P.

Curve
C (with locally constant curvature) and its circle of curvature in the extreme
P.
The circle of curvature (also known as the osculating circle or osculating circle ) at a certain point on a flat curve is the circle that best approximates the curve at this point. The center of the circle of curvature is called the center of curvature .

Its radius , the radius of curvature , is the amount of the reciprocal of the curvature of the curve in . Its tangent at this point coincides with the tangent of the curve.

Since the curvature of a curve generally varies locally, the circle of curvature usually only hugs the given curve in an infinitesimally small area. It runs on one side of the contact point inside and on the other side outside the curve , so it intersects the curve at a certain distance from . Only when the curvature of the curve has an extreme at the given point does the circle nestle against the curve over a longer stretch of the curve and does not change the side of the curve; there is then no intersection between the curve and the circle of curvature.




determination
The center point of the circle of curvature is the limit position of the intersection of the normals of the curve when the points of the normals strive towards each other:

t
1 , t
2 , ... are the tangents, n
1 , n
2 , ... are the normals in the points P
1 , P
2 , ... The points P
1 , P
2 , ... approach each other the vertex S. The intersection points K
1 , K
2 , ... approach the center of curvature K
If the curve is given in the parametric representation , its radius, the radius of curvature, is given by

- (1) .

The center of the circle of curvature then has the coordinates


The amount of the radius for determining the center point must be omitted so that the circle of curvature lies on the correct side of the curve! So
- (2) and

- (3) .

The path that the centers of the circles of curvature describe is called the evolute of the curve.
Radius of curvature of a function graph
A radius of curvature can also be specified for the graph of a function . The curvature of the function at the point
is understood to be the curvature of the graph of the function in the point . With the transformation and the function is transferred to a parametric representation and it is:







-
 .
.
The derivatives are:
-
 and .
and .
Thus the following applies for the radius of curvature of a function graph at the point after insertion in (1):


- (4) .

For the center of the circle of curvature:

- (5)

- (6)

Examples
circle

Animation of the curvature of a circle of radius 2, run through clockwise
The parametric representation of a circle is:

The derivatives are:
-
 ;
; 
-
 ;
; 
Inserted into (1) it follows for the radius of curvature of a unit circle with a radius of one:
- The radius of curvature of a circle is constant and is as large as its radius, r = 1.
The adjacent animation shows the circle of radius 2, traversing at constant speed 1 in a clockwise direction. He has parametric representation

and constant curvature equal . Its radius of curvature is constantly equal to 2, that is, equal to its radius. (The "acceleration vector" in this animation is the second derivative .)


parabola
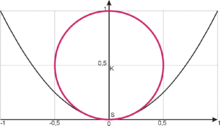
The circle of curvature of a normal parabola at its apex has a radius of 0.5
The following applies to the normal parabola :



If we insert into (4), it follows for the radius of curvature:

At the point x = 0 the radius of curvature is r = 0.5 (see figure). For large x the radius of curvature ~ x 3 increases , the curve becomes straighter and straighter.
Lissajous curve

Animation of the circle of curvature for a Lissajous curve
The parametric plot of a Lissajous curve with a frequency ratio of 2: 3 is

The first derivatives are:

The second derivatives are:

If you insert this in (1) and use the addition theorems for sine and cosine, then it follows for the radius of curvature of this Lissajous curve:

The illustration shows an animation of the circle of curvature. The "acceleration vector" in this figure is the second derivative of after the arc length .



See also
-
Clothoid , the radius of curvature is inversely proportional to the length of the curve
-
Snuggly ball , a generalization on space curves
literature
Web links














































