Shift register with linear feedback
A linear feedback shift register (Engl. Linear feedback shift register , just LFSR ) is a feedback shift register , which for the generation of strictly deterministic pseudo-random number sequences can be used. The linear logic function XOR is used for feedback .
The starting value is called the seed . Since the output of the register is strictly deterministic and depends entirely on its current state, but the register only has a finite number of states at the same time, it must inevitably arrive at its starting value at some point. With shift registers having a width of n bits, this results in a maximum period length of 2 n −1. From this point on, the output sequence is repeated, the register is in a repeat cycle. Depending on the chosen implementation, this sequence is of different length; at most, sequences of maximum length can be generated.
In addition to the generation of pseudo-random number sequences, applications are in the field of fast digital synchronous counters, since these counters work without carryover, in the field of communications technology and cryptography in scramblers to make data sequences spectrally white , in coding theory in the coding and decoding of cyclic codes , such as in the cyclical redundancy check (CRC) or the Hamming code , and in the field of digital modulation technology in the code division multiplex method (CDMA) and in the field of steganography .
Shift registers with linear feedback can be efficiently implemented both directly in hardware, such as FPGAs , and in software. In the software implementation, since most processors work with register widths larger than one bit, work is typically carried out with tables calculated in advance, which directly map the internal state of the shift register.
function
An LFSR is implemented in digital technology as a shift register with n storage elements. The individual storage elements are typically D flip-flops , each of which can store one bit. In contrast to a normal shift register, there are branches between certain D flip-flops, which represent the feedback. The number and position of these branches in the register chain is determined by a primitive polynomial , the so-called generator polynomial , in order to achieve the maximum possible period length of 2 n −1 . In this case, n is also equal to the degree of the generator polynomial.
A primitive polynomial as generator polynomial is not absolutely necessary, but non-primitive polynomials result in shorter period lengths. However, shorter period lengths can also be achieved with a smaller number of flip-flops and the use of a corresponding primitive polynomial of a lower degree, which is why practically only primitive polynomials are used as generator polynomials.
For initialization, in English this start value is also referred to as seed , the shift register can be filled with any values with XOR feedback - but not only with zeros, since then the register would never come out of this state, the shift register a trivial sequence of constant zeros would generate. Instead of the XOR links, XNOR links can also be used; In this case, all values except all ones are allowed as starting values, which again results in a maximum period length of 2 n −1. Depending on the technology, it is easier to implement the state with all zeros as the defined initial state. Linking by means of XNOR has the advantage that this state with all zeros is suitable as a starting value and does not lead to the trivial constant zero sequence, as with XOR.
An LFSR can also be implemented so that it has the maximum period length of 2 n . In this case, after one pass, all '0' appear in the shift register, which as a special case must be recognized by an additional logic circuit and compensated for by inverting the feedback, which is then activated. This possibility is also available with XNOR links; the special case here is instead the state with all ones.
Like any other shift register, the LFSR also has a clock input : With each clock pulse, there is a change to the next state and 2 n −1 clock pulses are required for a complete cycle of all combinations (if, as described above, a primitive polynomial is used and the mentioned “drilling out” of the feedback to 2 n states was dispensed with).
Because of its linearity of the sequences generated, an LFSR forms a poor pseudo-random number generator on its own for cryptological applications . LFSR are used as a primitive and in conjunction with nonlinear functions or as a combination of several LFSRs.
Besides the usual in digital circuits binary LFSR in GF (2) also exist non-binary LFSR with a number of elements q is larger than 2. The XOR operation, it represents an addition modulo represents 2, in the general case by an addition modulo q replaced , The storage elements must be able to store q states.
species
There are two different types of LFSR to be implemented:
- Fibonacci-LFSR, named after the Italian mathematician Leonardo Fibonacci , and
- Galois-LFSR, named after the French mathematician Évariste Galois .
Both types are equivalent to each other and have the same period lengths, although the sequences generated are different. They differ in their implementation, as shown in the figures, with CLK representing the clock input and Y the output of the LFSR. The XOR operators are shown with " ".
The two forms result from the fact that every primitive polynomial of degree n > 2 has a “twin polynomial ”, which is also primitive. In the two figures, a generator polynomial of the 8th degree was used for the Fibonacci LFSR:
The branch points correspond directly to the exponents. The equivalent primitive generator polynomial of the 8th degree in the Galois LFSR is:
Which of the two equivalent forms is specifically chosen depends, among other things, on optimizations in the implementation. For example, the three exclusive-or gates with two inputs each can be combined in the Fibonacci structure to form an exclusive-or gate with four inputs. This form can be efficiently implemented in FPGAs with lookup tables that have four inputs.
Polynomial selection
In addition to the degree n, which defines the period length, with a certain degree n > 2 there are always several primitive polynomials which are equivalent to one another. Further selection criteria can be added depending on the application. For example, so-called sparse generator polynomials are preferred in the field of scramblers in communications engineering . These are polynomials which manage with a minimum number of feedback points or with a minimum number of digits other than 1 in the generator polynomial. The reason for this is to minimize the hardware expenditure and, with self-synchronizing scramblers, the multiplication of reception errors in the descrambler. In the field of coding theory, such as cyclic codes (CRC) or cryptographic applications, however, densely populated polynomials are preferred according to other selection criteria.
Primitive polynomials of different degrees are listed in tables. In the following table some primitive polynomials with minimal occupation are listed:
| Degree | Exponents | Degree | Exponents | |
|---|---|---|---|---|
| 1 | 1 | 14th | 14, 13, 11, 9 | |
| 2 | 2, 1 | 15th | 15, 14 | |
| 3 | 3, 2 | 16 | 16, 14, 13, 11 | |
| 4th | 4, 3 | 17th | 17, 14 | |
| 5 | 5, 3 | 18th | 18, 11 | |
| 6th | 6, 5 | 19th | 19, 18, 17, 14 | |
| 7th | 7, 6 | 20th | 20, 17 | |
| 8th | 8, 6, 5, 4 | 21st | 21, 19 | |
| 9 | 9, 5 | 22nd | 22, 21 | |
| 10 | 10, 7 | 23 | 23, 18 | |
| 11 | 11, 9 | 24 | 24, 23, 21, 20 | |
| 12 | 12, 11, 8, 6 | ... | ... | |
| 13 | 13, 12, 10, 6 | 9689 | 9689, 84 |
Applications
Applications of LFSRs are, besides the above-mentioned areas in Modulo - counters which count up to the period length and then "overrun", so start all over again. This is significantly more efficient than an arithmetic (“real”) counter with carry logic, since instead of an n-bit addition, only a few exclusive-or operations (XOR) are required. However, the current counter reading cannot be derived directly from the state of the LFSR, which is why an LFSR counter is only suitable for certain applications, e.g. B. for index calculation when implementing a queue ( first in - first out ) using random access memory (RAM).
In the field of digital signal processing, LFSR are also differentiated according to the clock speed in relation to the bit rate or symbol rate in the applications. In the case of a scrambler , the bit rate or symbol rate is equal to the clock speed of the LFSR. If the LFSR is used for spectral spreading, the clock rate of the LFSR is significantly higher than the bit or symbol rate. This is used, for example, in the context of direct sequence spread spectrum methods (DSSS) or - related to this - in the field of code division multiple access (CDMA). So-called composite LFSRs can then be used to form sequences such as those used for navigation purposes within the framework of the Global Positioning System (GPS).
With linear feedback shift registers, compressed bit vectors are determined in the signature analysis to check the function of a circuit.
Compound LFSR
The combinations of the data sequences of different types of LFSR represent an extension. The resulting new data sequences can have different properties than the original LFSR. They can therefore be more suitable for applications in the code division multiple access and for spectral spreading due to a low autocorrelation .
The composition of the output data sequence from the individual independent LFSRs is carried out by means of an XOR link between the individual partial sequences. If the LFSR have different sequence lengths L = 2 n −1 and different generator polynomials , code sequences with completely new properties can be generated. As a rule, these composite, cyclical sequences do not have the maximum possible length. Some important classes of code sequences composed of LFSR registers are shown below:
Gold consequences
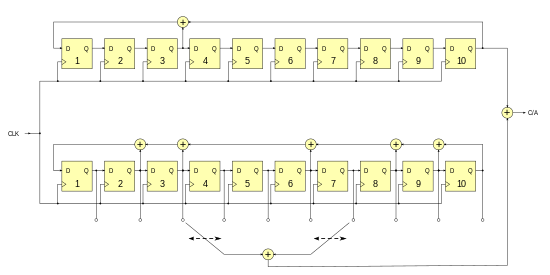
Gold sequences were introduced by Robert Gold in 1967 and also have two LFSRs with different generator polynomials, but of the same length m. The maximum code sequence length of the Gold sequence is therefore only 2 m −1. If you keep the initial state of one LFSR and change the initial state ("phase shift") of the other cyclically, 2 m −1 new code sequences can be created, all of which have a relatively small periodic cross-correlation maximum to one another, i.e. that is, they are almost orthogonal to one another. This means that these code sequences can be used in the area of code division multiple access (CDMA) and thus enable a distinction depending on the Gold sequence used.
The gold sequences are the spread spectrum signals most frequently used in practice because of their simple generation. In addition to mobile radio systems ( UMTS ) that work with CDMA, areas of application are also the civilly usable C / A code of the global positioning system GPS and WLANs .
Kasami episodes
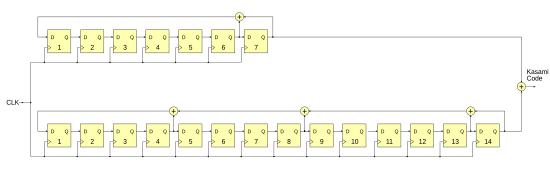
Kasami sequences were introduced by Tadao Kasami in 1966 and have a relatively small periodic cross-correlation maximum to one another, i.e. This means that they are almost orthogonal to one another and, like the Gold sequences, are used in the code division multiplex (CDMA) area. These LFSRs are used in code division multiplexing (CDMA) such as in the Russian position system GLONASS, where Kasami code sequences are used from the GLONASS-K satellite generation .
Kasami code sequences are generated by first forming a maximum sequence, decimating it, and repeatedly linking the thus decimated sequence with the maximum sequence using an XOR operation. There are two groups of Kasami code sequences, the small group and the large group. The small group consists of two LFSRs, the large group consists of three LFSRs.
To produce a Kasami code sequence from the small group of an LFSR is taken, shown in the right circuit below which the sequence of generated. The restriction must be straight. A second LFSR, shown above, generates the sequence with the index factor . The final Kasami sequence is formed by XORing the two partial sequences with one another:
The Kasami sequence has a length of . As a special feature, Kasami sequences only take the following four values for both cross-correlation and autocorrelation , if the generated code sequence is represented with the elements :
JPL episodes
JPL sequences consist of two LFSRs whose code sequence lengths L a and L b must be coprime. In this case the code sequence length of the generated overall sequence L c is equal to:
More than two LFSRs can also be interconnected using multiple XORs at the output. All the code sequence lengths of the individual LFSR must be coprime to one another.
JPL sequences were developed in the Jet Propulsion Labs , from which the name for these code sequences is derived. Areas of application include in the area of distance measurement using spread spectrum signals for satellites and in the area of space technology and with the more precise P / Y code used by the military in the global positioning system GPS .
See also
literature
- Uwe Meyer-Baese: Digital Signal Processing with Field Programmable Gate Arrays . 1st edition. Springer, 2001, ISBN 3-540-41341-3 .
Individual evidence
- ^ Manfred Schroeder: Number Theory in Science and Communication . 8th edition. Springer, 2008, ISBN 978-3-540-85297-1 .
- ^ Wayne Stahnke: Primitive Binary Polynomials . In: Mathematics of Computation . October 1973, p. 977-980 .
- ↑ Peter Alfke: Efficient Shift Registers, LFSR Counters, and Long Pseudo-Random Sequence Generators (= Xilinx Application Note XAPP052 ). 1996 ( online PDF).
- ^ Robert Gold: Optimal binary sequences for spread spectrum multiplexing . 4th edition. Volume 13. IEEE Transactions on Information Theory, pp. 619-621 ( online ).
- ^ Tadao Kasami: Weight Distribution Formula for Some Class of Cyclic Codes (= Technical Report No. R-285 ). University of Illinois, 1966.





![on]](https://wikimedia.org/api/rest_v1/media/math/render/svg/afec81633a396ebf2e4c5f53e3ef5bac8ee9f55f)


![b [n] = a [q \ cdot n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/60bbf9e419386eae6bcb9c987d0377c6c2766389)

![k [n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5c1873517b1d72811a73e453ab5def1aad036f1)
![k [n] = a [n] \ oplus b [n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/314d4269a54d86f958ff206d49a7f868b367592f)



