Magnetic circle

A magnetic circuit is a closed path of a magnetic flux  Φ . The consideration of magnetic circles plays an essential role , especially in the construction of electric motors , transformers and electromagnets . Coupling processes between the individual components of the magnetic circuits are of particular relevance here.

Elements of a magnetic circuit

A magnetic circuit can be divided into two types of signals:

• the magnetic flux and
• the magnetic tension,

and distinguish between three basic types of components:

• the magnetic conductor
• the magnetic resistance with the special case of the magnetic isolator and
• magnetic coupling elements

The physical content of the presentation in the article follows the context as presented in. The presentation of the authors Lenk, Pfeifer and Wertützky follows in their systematics.

Magnetic river

Coil as a coupling element between the magnetic circuit and the electrical circuit

The magnetic flux is usually introduced into the magnetic circuit with a coil as a coupling element. According to its name, the magnetic flux is a so-called "flux coordinate". When the magnetic circuit branches, the magnetic flux behaves according to the Kirchhoff equation and is divided into the individual sub-branches.

The relationship between the electrical voltage and the magnetic flux is provided by the law of induction in the transformed representation with complex numbers: ${\displaystyle U}$ ${\displaystyle \Phi }$

${\displaystyle \Phi ={\frac {U}{j\omega N}}}$

Here j is the imaginary unit, ω = 2πf the angular frequency and N the number of turns of the coil.

Magnetic voltage V _m and magnetic flux Θ

The magnetic voltage is defined as the line integral over the magnetic field strength H between two points P1 and P2 along the path s.

${\displaystyle V_{m}:=\int _{P1}^{P2}{\vec {H}}\mathrm {d} {\vec {s}}}$

The magnetic voltage is generally caused by electrical currents and introduced into the magnetic circuit via the coupling element coil. However, it must be taken into account that the electrical currents do not cause a magnetic voltage between two points, but a so-called magnetic circulation voltage or magnetic flux . This is a magnetic tension along a closed path. To distinguish it from the magnetic voltage, the circulating magnetic voltage is designated with the letter and written ${\displaystyle \Theta }$

${\displaystyle \Theta :=\oint {\vec {H}}\mathrm {d} {\vec {s}}}$

The peculiarity of the existence of a circulating voltage is that the magnetic voltage between two points depends on the path traveled (non-conservative field), so that the Kirchhoff's rule of meshes for magnetic voltages cannot generally be applied. In the model of the magnetic circuit, however, Kirchhoff's mesh rule is "saved" by the agreement that no integration paths through coil windings are taken into account when applying the mesh rule, thus avoiding internal contradictions of the theory.

Since the coupling coil is usually wound over a magnetically highly conductive magnetic core , simplified assumptions can be made for calculating the magnetic voltage. Because if there is only a vanishing magnetic field strength H in the magnetic core, the relevant portion of the magnetic voltage generated by the coil currents falls exclusively outside the magnetic core. ${\displaystyle \oint Hds}$

A coil current that winds N times around a magnetically highly conductive magnetic core causes a magnetic voltage of the magnitude outside the coil under these circumstances ${\displaystyle I}$ ${\displaystyle V_{m}}$

${\displaystyle V_{m}=N\cdot I}$

with the reference direction indicated in the drawing.

Magnetic conductors

Magnetically highly conductive connecting elements are the analogue of the metallic connecting line in an electrical circuit .

Magnetic conductors are characterized by the fact that the ratio of the magnetic voltage and the magnetic flux in the magnetic conductor material is almost equal to zero ${\displaystyle V_{m}}$ ${\displaystyle \Phi }$

${\displaystyle {\frac {V_{m}}{\Phi }}\to 0}$

An example of a magnetic conductor is the magnetic core in a transformer or a coil . The decisive condition for magnetically conductive materials is a high value for the relative permeability number . The relative permeability figure indicates the magnetic conductivity of the respective substance in comparison to the vacuum. Typical values ​​for ferromagnetic core materials in coils and transformers are in the range . ${\displaystyle \mu _{r}}$ ${\displaystyle 300<\mu _{r}<10.000}$

Magnetic resistances

Fastening elements made of materials with poor magnetic conductivity such as paramagnetic or diamagnetic materials are called magnetic resistors .

Magnetic resistances are characterized by the fact that the ratio of the magnetic voltage and the magnetic flux is a finite real number ${\displaystyle V_{m}}$ ${\displaystyle \Phi }$

${\displaystyle R_{mag}:={\frac {V_{m}}{\Phi }}<\infty }$

is.

They are the analogue of electrical resistance . An example of magnetic reluctance is a brief interruption in the magnetic core material of a transformer by an air gap. Superconductors have a permeability number and are therefore ideal magnetic insulators. ${\displaystyle \mu _{r}=0}$

Electric coil as a magnetic coupling element

Four-pole representation of the coupling between an electrical circuit and a magnetic circuit with a coil

With the help of coupling elements, the effect of networks from other physical areas can be brought into the magnetic circuit. A coupling element that is particularly frequently used in the magnetic circuit is the electrical coil. It links electrical circuits with the magnetic circuit and transfers energy between the two networks.

The coupling matrix between the electrical quantities and the magnetic quantities results from:

${\displaystyle {\begin{pmatrix}{I}\\{U/(j\omega )}\end{pmatrix}}={\begin{pmatrix}{0}&{1/N}\\{N}&{0}\end{pmatrix}}{\begin{pmatrix}{\Phi }\\{V_{m}}\end{pmatrix}}}$

Here the imaginary unit is the angular frequency and the number of turns of the coil. In a time-dependent representation, the expression denotes the time integral of the electrical voltage - the so-called voltage-time area . ${\displaystyle j}$ ${\displaystyle \omega =2\pi f}$ ${\displaystyle N}$ ${\displaystyle U/(j\omega )}$

Because the electric coil

• an electrical potential quantity ( ) into a magnetic flux quantity ( ) and ${\displaystyle U/(j\omega )}$ ${\displaystyle \Phi }$
• an electrical flux quantity ( ) into a magnetic potential quantity ( ) ${\displaystyle I}$ ${\displaystyle V_{m}}$

transferred, it is also said that the coil is a gyratory coupling element. A special description of the gyrator as a purely electrical (active) coupling element can be found in the associated Wikipedia article. Küpfmüller provides a general description in the context of the four-pole theory in Chapter 5.5, and Lenk in the context of the electromechanical and electroacoustic network theory.

In order to understand the effect of electrical components on the magnetic circuit, the electrical quantities can be converted into magnetic quantities using the transformation equations for the coil.

Transformation of an ohmic resistance

In the case of an electrical resistance R, there is a constant ratio of electrical voltage and electrical current . ${\displaystyle U}$ ${\displaystyle I}$

With the help of the transformation equations, a coil with N turns results in a magnetic impedance of:

${\displaystyle Z_{mag}={\frac {V_{m}}{\Phi }}={\frac {N\cdot I}{\frac {U}{j\omega N}}}=j\omega {\frac {N^{2}}{R}}}$

An electrical short circuit R = 0 therefore causes a magnetic open circuit, while an electrical open circuit causes a magnetic short circuit. The physical cause of the magnetic short circuit is based on the model assumption that the coil encloses a coil body with high magnetic conductivity.

It should be noted that electrical resistance across the coil will result in a magnetic impedance of the shape . The ohmic resistance at the coil therefore does not cause a magnetic resistance in the magnetic circuit, but rather a magnetic inductance . The authors Süße, Burger and others refer to the electrical resistance at the coupling element coil in a more generally applicable representation as an eddy current element and state: While the electrical resistance is an energy consumer, the magnetic resistance represents an energy store. In contrast, the inductance L is an energy store, and the eddy current element (magnetic inductance ) is an energy consumer. ${\displaystyle j\omega X}$ ${\displaystyle L_{m}}$ ${\displaystyle R}$ ${\displaystyle R_{m}}$ ${\displaystyle L_{m}}$

Transformation of an electrical inductance

An electrical inductance L leads to a purely real magnetic resistance with a positive sign in the magnetic circuit :

${\displaystyle Z_{mag}={\frac {V_{m}}{\Phi }}={\frac {N\cdot I}{\frac {U}{j\omega N}}}=j\omega {\frac {N^{2}}{j\omega L}}={\frac {N^{2}}{L}}}$

Transformation of an electrical capacitance

An electrical capacitance C leads to a purely real magnetic resistance with a negative sign in the magnetic circuit:

${\displaystyle Z_{mag}={\frac {V_{m}}{\Phi }}={\frac {N\cdot I}{\frac {U}{j\omega N}}}=j\omega {\frac {N^{2}}{\frac {1}{j\omega C}}}=-\omega ^{2}N^{2}C}$

In principle, coupling elements to other physical areas such as mechanics can also be defined. For example, the change in the magnetic flux in a magnetic circuit with an air gap causes a change in force on the opposing pole faces. In his system-theoretical considerations, Lenk differentiates between three mechanical coupling principles: the electromagnetic principle, the electrodynamic principle and the piezomagnetic principle, for each of which separate coupling elements can be described. ${\displaystyle \Delta \Phi }$ ${\displaystyle \Delta F}$

Analogy to the electrical circuit

The laws of magnetic flux are defined analogously to the laws in the electrical circuit (see also analogy of electrical and magnetic quantities ). The magnetic flux Φ is in this case analogous to the electric current I , the reluctance R _m analogous to Resistance R and the magnetic voltage analogous to the electric voltage U considered. ${\displaystyle V_{m}}$

In analogy to electrical resistance, what is known as magnetic resistance can be found in a magnetic circuit

${\displaystyle R_{m}={\frac {V_{m}}{\Phi }}}$

define.

In many magnetic materials, the magnetic resistance is approximately constant. In this context one speaks of Ohm's law of the magnetic circuit

${\displaystyle {\frac {V_{m}}{\Phi }}=const}$.

The reluctance is defined by the magnetic conductivity and the geometric dimensions analogous to the resistivity:

${\displaystyle R_{m}={\frac {l}{\mu \,A}}={\frac {1}{G_{m}}}}$

In magnetic circuits, which are described by concentrated components, the kirchhoff laws also apply :

• ${\displaystyle \sum \Phi =0}$
• ${\displaystyle \sum V_{m}=0}$

Magnetic circles can be calculated using Kirchhoff's laws.

Comparison of some electrical and magnetic quantities

electrical size		magnetic size
electrical voltage	U	magnetic tension	${\displaystyle V_{m}}$
electrical current	I.	magnetic river	Φ
Resistance (electrical resistance)	R.	Reluctance (magnetic resistance)	R m
Conductivity (electrical conductivity)	γ	Permeability (magnetic conductivity)	μ
Conductance (electrical conductance)	G	Permeance (magnetic conductance)	G m

Examples

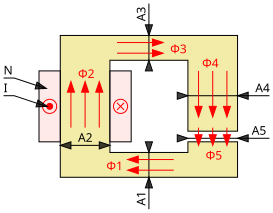
Magnetic circuit with air gap

Construction of a simple magnetic circuit

The illustration opposite shows the structure of a simple magnetic circuit. An electric current I flows through a winding with N turns and thus generates the magnetic flux density B ₂ . By

${\displaystyle \Phi _{2}=A_{2}\,B_{2}}$

you get the magnetic flux in the core of the winding. The core is used for the targeted spatial guidance of the magnetic flux in the magnetic circuit and is made of materials with high magnetic conductivity , such as a ferrite core .

In an ideal ferromagnetic material without leakage flux, the following applies:

${\displaystyle \Phi _{1}=\Phi _{2}=\Phi _{3}=\Phi _{4}=\Phi _{5}}$

However, since there are no ideal ferromagnetic materials in practice, losses occur as a result of the leakage flux. The exact calculation of these leakage fluxes is only rarely accessible analytically in a closed manner and it is usually done using computer-aided numerical approximation methods. In practice, the leakage losses on standardized magnetic cores are calculated with the help of previously determined coefficients σ:

${\displaystyle \Theta =N\,I=\sum _{n}V_{2,n}=\sum _{k}{R_{m,k}\,\Phi _{k}}=\sum _{k}{R_{m,k}\,{\frac {\Phi _{2}}{\sigma _{k}}}}}$

where V _{2, n represent} the magnetic voltages of the individual sections.

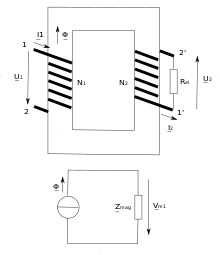
Two winding transformer

Transformer as a magnetic circuit

In the model of the magnetic circuit, the transformer fed with the voltage with the secondary-side electrical load results as a simple circuit, the one with the magnetic flux ${\displaystyle U_{1}}$ ${\displaystyle R_{el}}$

${\displaystyle \Phi ={\frac {U_{1}}{j\omega N_{1}}}}$

is fed.

The magnetic voltage results according to the component law for the magnetic impedance as follows: ${\displaystyle Z_{mag}}$

${\displaystyle V_{m}=Z_{mag}\Phi =j\omega {\frac {N_{2}^{2}}{R_{el}}}\cdot {\frac {U_{1}}{j\omega N_{1}}}}$

With the help of the equation , the electrical current in the secondary winding can be calculated ${\displaystyle V_{m}=N_{2}\cdot I_{2}}$

${\displaystyle I_{2}={\frac {N_{2}}{N_{1}}}{\frac {U_{1}}{R_{el}}}}$,

which corresponds to the known transformation equations for the transformer.

Transformer with two parallel load circuits

Transformer with two parallel load circuits in the model of the magnetic circuit

The advantages of modeling, which are analogous to the electrical circuit, only emerge with branched magnetic circuits.

The voltage source creates a magnetic flux ${\displaystyle U_{1}}$

${\displaystyle \Phi _{1}={\frac {U_{1}}{j\omega N_{1}}}}$

which is divided into the two partial flows and according to the junction equation for the magnetic circuit . ${\displaystyle \Phi _{2}}$ ${\displaystyle \Phi _{3}}$

${\displaystyle \Phi _{1}=\Phi _{2}+\Phi _{3}}$

The division can be calculated from the AC bill using the flow divider rule. The following results for the two sub-flows:

${\displaystyle \Phi _{2}={\frac {Z_{mag3}}{Z_{mag2}+Z_{mag3}}}\cdot \Phi _{1}={\frac {Z_{mag3}}{Z_{mag2}+Z_{mag3}}}\cdot {\frac {U_{1}}{j\omega N_{1}}}}$

${\displaystyle \Phi _{3}={\frac {Z_{mag2}}{Z_{mag2}+Z_{mag3}}}\cdot \Phi _{1}={\frac {Z_{mag2}}{Z_{mag2}+Z_{mag3}}}\cdot {\frac {U_{1}}{j\omega N_{1}}}}$

If one sets the component relationships

${\displaystyle Z_{mag2}=j\omega {\frac {N_{2}^{2}}{R_{2}}}}$ and

${\displaystyle Z_{mag3}=j\omega {\frac {N_{3}^{2}}{R_{3}}}}$

one, the voltages and currents in the two passive windings result from this.

The following applies to the stresses:

${\displaystyle U_{2}=j\omega N_{2}\Phi _{2}=j\omega N_{2}\cdot {\frac {Z_{mag3}}{Z_{mag2}+Z_{mag3}}}\cdot {\frac {U_{1}}{j\omega N_{1}}}={\frac {N_{2}}{N_{1}}}U_{1}\cdot {\frac {\frac {N_{3}^{2}}{R_{3}}}{{\frac {N_{2}^{2}}{R_{2}}}+{\frac {N_{3}^{2}}{R_{3}}}}}={\frac {N_{2}}{N_{1}}}U_{1}\cdot {\frac {R_{2}N_{3}^{2}}{R_{3}\cdot N_{2}^{2}+R_{2}N_{3}^{2}}}}$

and accordingly

${\displaystyle U_{3}={\frac {N_{3}}{N_{1}}}U_{1}\cdot {\frac {R_{3}N_{2}^{2}}{R_{3}\cdot N_{2}^{2}+R_{2}N_{3}^{2}}}}$

Due to the parallel connection, there are identical magnetic tensions on both branches:

${\displaystyle V_{m2}=V_{m3}=\Phi _{1}\cdot {\frac {Z_{mag2}\cdot Z_{mag3}}{Z_{mag2}+Z_{mag3}}}={\frac {U_{1}}{j\omega N_{1}}}\cdot {\frac {j\omega {\frac {N_{2}^{2}}{R_{2}}}\cdot {\frac {N_{3}^{2}}{R_{3}}}}{{\frac {N_{2}^{2}}{R_{2}}}+{\frac {N_{3}^{2}}{R_{3}}}}}={\frac {U_{1}}{N_{1}}}\cdot {\frac {{\frac {N_{2}^{2}}{R_{2}}}\cdot {\frac {N_{3}^{2}}{R_{3}}}}{{\frac {N_{2}^{2}}{R_{2}}}+{\frac {N_{3}^{2}}{R_{3}}}}}={\frac {U_{1}}{N_{1}}}{\frac {N_{2}^{2}N_{3}^{2}}{N_{2}^{2}R_{3}+N_{3}^{2}\cdot R_{2}}}}$

With the help of for the currents we get : ${\displaystyle V_{m}=\Theta =N\cdot I}$

${\displaystyle I_{2}={\frac {U_{1}}{N_{1}N_{2}}}{\frac {N_{2}^{2}N_{3}^{2}}{N_{2}^{2}R_{3}+N_{3}^{2}\cdot R_{2}}}}$

${\displaystyle I_{3}={\frac {U_{1}}{N_{1}N_{3}}}{\frac {N_{2}^{2}N_{3}^{2}}{N_{2}^{2}R_{3}+N_{3}^{2}\cdot R_{2}}}}$

literature

• Horst Stöcker: Pocket book of physics. 4th edition. Verlag Harry Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4 .
• Hans Fischer: Materials in electrical engineering. 2nd Edition. Carl Hanser Verlag, Munich / Vienna 1982, ISBN 3-446-13553-7 .
• Günter Springer: Expertise in electrical engineering. 18th edition. Verlag Europa-Lehrmittel, Wuppertal 1989, ISBN 3-8085-3018-9 .

Individual evidence

1. ↑ Siegfried Altmann, Detlef Schlayer: Text and exercise book electrical engineering. Hanser-Verlag, 2008, ISBN 978-3-446-41426-6 , books.google.de
2. ↑ ^{a b c} A. Lenk, G. Pfeiffer, R. Werthschützky: Electromechanical systems. Springer, New York 2001, ISBN 3-540-67941-3 , books.google.de .
3. ^ Paul Dobrinski, Gunter Krakau, Anselm Vogel: Physics for engineers. 11th edition. Teubner-Verlag, 2007, ISBN 978-3-8351-0020-6 , p. 304, books.google.de
4. ↑ Marlene Marinescu: Electric and Magnetic Fields - A Practice-Oriented Introduction. Springer, 2009, ISBN 978-3-540-89696-8 , p. 173, books.google.de
5. ↑ Marlene Marinescu: Electric and Magnetic Fields - A Practice-Oriented Introduction. Springer, 2009, ISBN 978-3-540-89696-8 , p. 218, books.google.de
6. ↑ Küpfmüller, Mathis, Reibiger: Theoretical electrical engineering. Chapter 5.5 books.google.de
7. ↑ Roland Süße, Peter Burger, Ute Diemar, Eberhard Kallenbach: Theoretical foundations of electrical engineering. Volume 2, Vieweg + Teubner, ISBN 978-3-519-00525-4 , p. 484, books.google.de