Simpson's rule

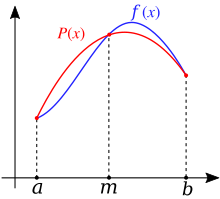
The Simpson rule or Simpson's formula (after Thomas Simpson ), sometimes also Kepler's barrel rule (after Johannes Kepler ) is a method of numerical integration in which an approximation to the integral of a function in the interval is calculated by replacing the difficult-to-integrate function with an exact integrable parabola approximates. ${\displaystyle f(x)}$ ${\displaystyle [a,b]}$ ${\displaystyle f(x)}$ ${\displaystyle P(x)}$

Simpson's formula

The parabola is placed as an interpolation polynomial by function values ​​at the points , and . The integral is then approximated by the integral of the parabola. The Simpson rule is thus a so-called closed Newton-Cotes formula . The approximation of then results in: ${\displaystyle P(x)}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle m={\tfrac {a+b}{2}}}$ ${\displaystyle S(f)}$ ${\displaystyle \int _{a}^{b}f(x)dx}$

${\displaystyle S(f)={\frac {b-a}{6}}\cdot \left(f(a)+4f(m)+f(b)\right).}$

history

The formula was first used by Evangelista Torricelli , born in 1608, but is named after the English mathematician Thomas Simpson, born in 1710. It corresponds to Kepler's barrel rule, which Johannes Kepler established in 1615.

Kepler reports on the genesis in the dedication of the later publication. After Kepler's first wife died in Prague in 1611, he remarried in 1613 - now working in Linz. He bought some barrels of wine for the wedding. When the wine was in the cellar, the seller came with a measuring rod and determined the contents of all the barrels using the same method without consideration or calculation. The metal tip of the measuring rod was inserted through the bunghole across to the edges of the two floors and the mark on the bunghole gave the volume. Kepler was surprised that a diagonal through the barrel half should provide a measure of the volume, and doubted the correctness of this method, since a very low barrel with slightly wider bottoms and therefore much smaller volume could have the same sight length.

Kepler then wrote the font Nova Stereometria doliorum vinariorum 1615 (New calculation of the content of wine barrels), in which he looked for verifiable methods for calculating the content of wine barrels. One of these methods consisted in approximating the curvature of the barrel by means of a parabola, since content calculations with the help of parabolas could be carried out exactly since Archimedes .

Among other things, he described a formula for calculating the capacity (more precisely the volume ) of wine barrels with irregular shapes. This formula provides exact values ​​for the circular cylinder , truncated cone (including cone ), sphere , ellipsoid of revolution , elliptical paraboloid, and single-shell hyperboloid .

example

${\displaystyle J(f)=\int _{0}^{2}3^{3x-1}\,\mathrm {d} x=\left.{\frac {3^{3x-2}}{\ln(3)}}\right|_{0}^{2}={\frac {728}{9\ln(3)}}=73{,}6282396649\dots }$

With the help of the Simpson rule explained below, this specific integral is to be calculated approximately.

Error estimation

The remainder term (alternatively the quadrature error ) describes the difference between the actual integral and the approximation using Simpson's rule: ${\displaystyle E(f)}$

${\displaystyle J(f)=\int _{a}^{b}f(x)\,\mathrm {d} x=S(f)+E(f).}$

If four times continuously differentiable in , then the estimate applies to the remainder of the term ${\displaystyle f(x)}$ ${\displaystyle [a,b]}$ ${\displaystyle E(f)}$

${\displaystyle \left|E(f)\right|\leq {\frac {(b-a)^{5}}{2880}}\max _{a\leq x\leq b}{\left|f^{(4)}(x)\right|}.}$

If it is also real-valued, then with a suitable intermediate point from applies for the remainder ${\displaystyle f(x)}$ ${\displaystyle \zeta }$ ${\displaystyle [a,b]}$

${\displaystyle E(f)=-{\frac {(b-a)^{5}}{2880}}{f^{(4)}(\zeta )}.}$

This representation of the remaining limbs was found by Giuseppe Peano in 1887 . In particular, it says that the Simpson rule integrates polynomials of degree three exactly, i.e. one degree higher than one would expect from construction. All (closed and open) Newton-Cotes formulas of even degree have this property.

Illustration through rectangular areas

Simpson's formula illustration

The integral of the approximate parabola is equal to the hatched area of ​​six rectangles, each of which is 1/6 of the interval . One rectangle has the height , one rectangle the height and four rectangles the height . ${\displaystyle [a,b]}$ ${\displaystyle f(a)}$ ${\displaystyle f(b)}$ ${\displaystyle f(m)}$

Here you can also see the connection with the tendon trapezoidal formula and the tangent trapezoidal formula ${\displaystyle T(f)={\frac {b-a}{2}}{\bigl (}f(a)+f(b){\bigr )}}$ ${\displaystyle M(f)=(b-a)\ f\left({\frac {a+b}{2}}\right)}$

While the two outer rectangles correspond to the approximation by the (1/3 scaled) chord trapezoidal formula, the remaining rectangles correspond to the tangent trapezoidal formula (scaled 2/3):

${\displaystyle S(f)={\frac {1}{3}}\left(T(f)+2M(f)\right).}$

Summed Simpson's formula

In order to be able to approximate the integral even better, the interval is divided into adjacent, equally large sub-intervals. In each sub-interval, the Simpson formula is used for the individual sub-areas and then the resulting approximations are added. This gives the summed or compound Simpson rule. There are different notations for the subdivision into sub-intervals, which lead to different formulations of the summed Simpson's formula. ${\displaystyle [a,b]}$

version 1

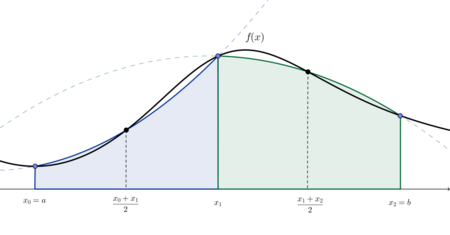
Summed up Simpson's formula for N = 2

Here the interval is divided into adjacent, equally large sub-intervals of length . The Simpson formula is used in each sub-interval and the resulting approximations are then added. With and you get: ${\displaystyle [a,b]}$ ${\displaystyle N}$ ${\displaystyle [x_{i},x_{i+1}]}$ ${\displaystyle h}$ ${\displaystyle {\frac {h}{6}}\cdot (f(x_{i})+4\cdot f\left({\frac {x_{i}+x_{i+1}}{2}}\right)+f(x_{i+1}))}$ ${\displaystyle h={\frac {b-a}{N}}}$ ${\displaystyle x_{k}=a+k\cdot h}$

${\displaystyle S^{(N)}(f)={\frac {h}{6}}\cdot \left(f(x_{0})+4\cdot f\left({\frac {x_{0}+x_{1}}{2}}\right)+2\cdot f(x_{1})+4\cdot f\left({\frac {x_{1}+x_{2}}{2}}\right)+\dotsb +2\cdot f(x_{N-1})+4\cdot f\left({\frac {x_{N-1}+x_{N}}{2}}\right)+f(x_{N})\right)}$

or.

${\displaystyle S^{(N)}(f)={\frac {h}{6}}\cdot \left(f(x_{0})+2\sum _{k=1}^{N-1}f(x_{k})+f(x_{N})+4\sum _{k=1}^{N}f\left({\frac {x_{k-1}+x_{k}}{2}}\right)\right)}$

example

Applied to the example above:

Be and thus the step size . Then ${\displaystyle N=3}$ ${\displaystyle h={\tfrac {2}{3}}}$

${\displaystyle {\begin{aligned}S^{(3)}(f)&={\frac {2}{18}}\left(f(0)+2\left(f\left({\frac {2}{3}}\right)+f\left({\frac {4}{3}}\right)\right)+f(2)+4\left(f\left({\frac {1}{3}}\right)+f\left({\frac {3}{3}}\right)+f\left({\frac {5}{3}}\right)\right)\right)\\&={\frac {2002}{27}}=74{,}{\overline {148}}\\\end{aligned}}}$

Be and thus the step size . Then ${\displaystyle N=6}$ ${\displaystyle h={\tfrac {2}{6}}={\tfrac {1}{3}}}$

${\displaystyle {\begin{aligned}S^{(6)}(f)&={\frac {1}{18}}\left(f(0)+2\left(f\left({\frac {1}{3}}\right)+f\left({\frac {2}{3}}\right)+f(1)+f\left({\frac {4}{3}}\right)+f\left({\frac {5}{3}}\right)\right)+f(2)\right)\\&+{\frac {1}{18}}\left(4\left(f\left({\frac {1}{6}}\right)+f\left({\frac {3}{6}}\right)+f\left({\frac {5}{6}}\right)+f\left({\frac {7}{6}}\right)+f\left({\frac {9}{6}}\right)+f\left({\frac {11}{6}}\right)\right)\right)\\&={\frac {1}{3}}\left(T^{(6)}(f)+2M^{(6)}(f)\right)={\frac {4\cdot T^{(12)}(f)-T^{(6)}(f)}{3}}={\frac {728\cdot ({\sqrt {3}}+1)}{27}}=73{,}66418473741264\dots \\\end{aligned}}}$

Here is the value of the tendon trapezoidal rule and the value of the tangent trapezoidal rule . ${\displaystyle T^{(6)}(f)}$ ${\displaystyle M^{(6)}(f)}$

Error estimation

The error estimate for the remainder is: ${\displaystyle E(f)=\int _{a}^{b}f(x)\,dx-Q(f)}$

${\displaystyle \left|E(f)\right|\leq {\frac {(b-a)}{2880}}h^{4}\max _{a\leq x\leq b}{\left|f^{(4)}(x)\right|},}$

or for real-valued functions with a suitable intermediate point from the interval ${\displaystyle \zeta }$ ${\displaystyle [a,b]}$

${\displaystyle E(f)=-{\frac {(b-a)}{2880}}h^{4}f^{(4)}(\zeta ).}$

The factor in the above formula means that if the step size is halved (doubling the intervals), as is the case with the Romberg method with the Romberg sequence, the error is approximately 16 times smaller, as the following example shows : ${\displaystyle h^{4}}$

example

Applied to the example above:

With follows ${\displaystyle f^{(4)}(x)=3^{3x+3}\cdot \ln(3)^{4}}$

${\displaystyle \max _{0\leq x\leq 2}\left|f^{(4)}(x)\right|=3^{3\cdot 2+3}\cdot \ln(3)^{4}=3^{9}\cdot (\ln(3))^{4}}$

and thus the error estimate

${\displaystyle \left|E^{(3)}(f)\right|\leq {\frac {2}{2880}}\cdot \left({\frac {2}{3}}\right)^{4}\cdot 3^{9}\cdot (\ln(3))^{4}={\frac {27\cdot (\ln(3))^{4}}{10}}=3{,}933\dotso }$,

which is expected to result in a larger value than the exact value

${\displaystyle E^{(3)}(f)=-0{,}5199\dotso .}$

The error estimate is obtained analogously

${\displaystyle \left|E^{(6)}(f)\right|\leq {\frac {2}{2880}}\cdot \left({\frac {1}{3}}\right)^{4}\cdot 3^{9}\cdot (\ln(3))^{4}={\frac {27\cdot (\ln(3))^{4}}{160}}=0{,}2458\dotso }$,

which is expected to result in a larger value than the exact value

${\displaystyle E^{(6)}(f)=-0{,}0359\dotso }$.

It applies

${\displaystyle \left|E^{(6)}(f)\right|=0{,}0359\dotso \approx {\frac {\left|E^{(3)}(f)\right|}{16}}={\frac {0{,}5199\dotso }{16}}=0{,}03249\dotso }$.

Error estimation

If you calculate the Simpson rule twice with 2 different numbers of intervals , you get the following error estimate: ${\displaystyle N\neq M}$

${\displaystyle E^{(N)}(f)\approx {\frac {M^{4}}{M^{4}-N^{4}}}\left(S^{(M)}(f)-S^{(N)}(f)\right).}$

Especially when doubling the intervals (halving the step size) one obtains the error estimate: ${\displaystyle M=2N}$

${\displaystyle E^{(N)}(f)\approx {\frac {16}{15}}\left(S^{(2N)}(f)-S^{(N)}(f)\right).}$

Applied to the above example one obtains

${\displaystyle {\begin{aligned}E^{(3)}(f)=-0{,}5199\dots &\approx {\frac {16}{15}}\left(S^{(6)}(f)-S^{(3)}(f)\right)\\&=-0{,}5162\dots .\end{aligned}}}$

Variant 2

Summed up Simpson's formula for N = 4

Here one divided interval in juxtaposed, equally large partial intervals with the center and length with . Since it is now twice as large as compared to variant 1, it is only half as large as compared to variant 1. This means that in all formulas of variant 1 this must be replaced by. ${\displaystyle [a,b]}$ ${\displaystyle n=N/2}$ ${\displaystyle [x_{i},x_{i+2}]}$ ${\displaystyle x_{i+1}}$ ${\displaystyle 2h}$ ${\displaystyle h={\frac {b-a}{N}}}$ ${\displaystyle N}$ ${\displaystyle h}$ ${\displaystyle h}$ ${\displaystyle 2h}$

For every straight line one applies the Simpson's formula to the interval ${\displaystyle i}$ ${\displaystyle [x_{i},x_{i+2}]}$

${\displaystyle {\frac {2h}{6}}\cdot (f(x_{i})+4\cdot f(x_{i+1})+f(x_{i+2}))={\frac {h}{3}}\cdot (f(x_{i})+4\cdot f(x_{i+1})+f(x_{i+2}))}$

and then adds the resulting approximations.

For straight now applies , and and we have: ${\displaystyle N}$ ${\displaystyle n=N/2}$ ${\displaystyle h={\frac {b-a}{N}}}$ ${\displaystyle x_{k}=a+k\cdot h}$

${\displaystyle S^{(n)}(f)={\frac {h}{3}}\left(f(x_{0})+4\cdot f(x_{1})+2\cdot f(x_{2})+4\cdot f(x_{3})+2\cdot f(x_{4})+\dotsb +4\cdot f(x_{N-1})+f(x_{N})\right).}$

or.

${\displaystyle S^{(n)}(f)={\frac {h}{3}}\left(f(x_{0})+2\sum _{k=1}^{n-1}f(x_{2k})+f(x_{2n})+4\sum _{k=1}^{n}f(x_{2k-1})\right)}$

example

Applied to the example above:

Be , and the stride . Then ${\displaystyle N=6}$ ${\displaystyle n=N/2=3}$ ${\displaystyle h={\tfrac {2}{6}}={\tfrac {1}{3}}}$

${\displaystyle {\begin{aligned}S^{(3)}(f)&={\frac {1}{9}}\left(f(0)+2\left(f\left({\frac {2}{3}}\right)+f\left({\frac {4}{3}}\right)\right)+f(2)+4\left(f\left({\frac {1}{3}}\right)+f\left({\frac {3}{3}}\right)+f\left({\frac {5}{3}}\right)\right)\right)\\&={\frac {2002}{27}}=74{,}{\overline {148}}\\\end{aligned}}}$.

This is the same result as in variant 1.

Error estimation

The error estimate for the remainder is now ${\displaystyle E^{(n)}(f)=\int _{a}^{b}f(x)\,dx-S^{(n)}(f)}$

${\displaystyle \left|E^{(n)}(f)\right|\leq {\frac {(b-a)}{2880}}(2h)^{4}\max _{a\leq x\leq b}{\left|f^{(4)}(x)\right|}={\frac {(b-a)}{180}}h^{4}\max _{a\leq x\leq b}{\left|f^{(4)}(x)\right|},}$

or for real-valued functions with a suitable intermediate point from the interval ${\displaystyle \zeta }$ ${\displaystyle [a,b]}$

${\displaystyle E^{(n)}(f)=-{\frac {(b-a)}{180}}h^{4}f^{(4)}(\zeta ).}$

Relation to other formulas

If one adds the error estimate for to the approximate value , one obtains the i. A. better formula: ${\displaystyle S^{(N)}(f)}$ ${\displaystyle E^{(N)}(f)}$

${\displaystyle R^{(N)}(f)=S^{(N)}(f)+{\frac {16}{15}}\left(S^{(2N)}(f)-S^{(N)}(f)\right)={\frac {16\cdot S^{(2N)}(f)-S^{(N)}(f)}{15}}.}$

This is the formula for the 3rd column of the calculation scheme of the Romberg integration when using the Romberg sequence and at the same time the result of the Milne rule (completed Newton-Cotes formula with degree of accuracy 5) when applied to sub-intervals of ${\displaystyle N}$ ${\displaystyle [a,b].}$

Applied to the above example one gets with

${\displaystyle R^{(3)}(f)={\frac {16\cdot S^{(6)}(f)-S^{(3)}(f)}{15}}={\frac {16\cdot 73{,}664\dots -74{,}{\overline {148}}}{15}}=73{,}63192\dots }$

a better approximation for the exact integral ${\displaystyle J(f)=\int _{0}^{2}3^{3x-1}\,\mathrm {d} x=73{,}6282396649\dots }$

than with or ${\displaystyle S^{(3)}(f)=74{,}{\overline {148}}}$ ${\displaystyle S^{(6)}(f)=73{,}664\dots ,}$

with the same number of function values ​​to be evaluated as with , namely 13 pieces. ${\displaystyle S^{(6)}(f)}$

Volume calculation

The name barrel rule can be justified by the following application: To calculate the volume of a wine barrel, let the cross-sectional area transverse to the longitudinal axis at the distance from the bottom of the barrel; it can be easily calculated by determining the scope. If the height of the barrel, the volume is the same ${\displaystyle q(x)}$ ${\displaystyle x}$ ${\displaystyle h}$

${\displaystyle V=\int _{0}^{h}q(x)\,\mathrm {d} x.}$

The Kepler barrel rule now applies

${\displaystyle V\approx {\frac {h}{6}}\cdot \left(q(0)+4q\left({\frac {h}{2}}\right)+q(h)\right)}$

as an approximation for the volume of a body whose cross-section is known in three places. If the body is a body of revolution, the following applies when the function is rotated around the x axis: ${\displaystyle g(x)}$

${\displaystyle {\begin{aligned}V&=\pi \cdot \int _{0}^{h}(g(x))^{2}\mathrm {d} x\\&\approx \pi {\frac {h}{6}}\cdot \left(\left(g(0)\right)^{2}+4\left(g\left({\frac {h}{2}}\right)\right)^{2}+(g(h))^{2}\right)\end{aligned}}}$

This formula gives the exact volume for certain solids of revolution such as a cone and truncated cone , cylinder , ellipsoid of revolution and paraboloid of revolution.

If the circumference of the base and lid and the circumference is in the middle of the barrel, this gives the approximate value ${\displaystyle u}$ ${\displaystyle U}$ ${\displaystyle N}$

${\displaystyle V\approx N=\pi {\frac {h}{6}}\cdot \left[2\left({\frac {u}{2\pi }}\right)^{2}+4\left({\frac {U}{2\pi }}\right)^{2}\right]\ =\pi {\frac {h}{6}}\cdot \left[2\left({\frac {u^{2}}{4\pi ^{2}}}\right)+4\left({\frac {U^{2}}{4\pi ^{2}}}\right)\right]={\frac {h}{12\pi }}\cdot \left[u^{2}+2U^{2}\right].}$

If the barrel has a parabolic curvature, the barrel is obtained by rotating the function around the x-axis. If you place the axis cross in the middle of the barrel for the sake of simplicity, the following applies ${\displaystyle g(x)=ax^{2}+bx+c}$

${\displaystyle g(x)=2{\frac {u-U}{\pi h^{2}}}x^{2}+{\frac {U}{2\pi }}.}$.

The exact value is obtained

${\displaystyle V=\pi \cdot \int _{-{\frac {h}{2}}}^{\frac {h}{2}}(g(x))^{2}\,\mathrm {d} x={\frac {h}{60\pi }}\cdot \left[3u^{2}+4Uu+8U^{2}\right].}$

As an error you get

${\displaystyle E(f)=V-N={\frac {h}{60\pi }}\cdot \left[3u^{2}+4Uu+8U^{2}\right]-{\frac {h}{12\pi }}\cdot \left[u^{2}+2U^{2}\right]=-{\frac {h}{30\pi }}\cdot (u-U)^{2}.}$

This example shows the validity of the formula given above

${\displaystyle E(f)=-{\frac {(b-a)^{5}}{2880}}{f^{(4)}(\zeta )}}$

verify well. Here is and ${\displaystyle b-a=h}$

${\displaystyle f(x)=\pi \cdot (g(x))^{2}=\pi \cdot \left({2{\frac {u-U}{\pi h^{2}}}}x^{2}+{\frac {U}{2\pi }}\right)^{2}}$

a polynomial of degree 4 with constant 4th derivative:

${\displaystyle f^{(4)}(x)={\frac {96\cdot (u-U)^{2}}{\pi \cdot h^{4}}}.}$.

For the error you get

${\displaystyle E(f)=-{\frac {h^{5}}{2880}}\cdot {\frac {96\cdot (u-U)^{2}}{\pi \cdot h^{4}}}=-{\frac {h}{30\pi }}\cdot (u-U)^{2}\leq 0,}$,

thus the same value as above.

The error is less than / equal to 0, so the approximation is greater than / equal to the exact volume . The error is greater, the more they differ and the more arched the barrel is. The error is 0 if and only if , i.e. if the barrel is a cylinder, in agreement with the above statement that the formula for cylinder is exact. ${\displaystyle N}$ ${\displaystyle V}$ ${\displaystyle u}$ ${\displaystyle U}$ ${\displaystyle u=U}$

Use as a Runge-Kutta method

The Simpson rule can also be represented as the Runge-Kutta method , using the Butcher scheme

${\displaystyle {\begin{array}{c|ccc}0&0&0&0\\{\frac {1}{2}}&{\frac {1}{2}}&0&0\\1&-1&2&0\\\hline &{\frac {1}{6}}&{\frac {4}{6}}&{\frac {1}{6}}\end{array}}.}$

literature

• Hans R. Schwarz, Norbert Köckler: Numerical Mathematics. 6th edition, Teubner, Stuttgart 2006, ISBN 3-519-42960-8 , pp. 311-316.
• Johannes Kepler: New stereometry of the barrels . Translated from Latin and edited by R. Klug. W. Engelmann. Leipzig, 1908.

Web links

Commons : Simpson's rule  - collection of pictures, videos and audio files

• Website of the museum room on Johannes Kepler of the Bundesrealgymnasium Kepler, Graz