Circulation (field theory)

The circulation is the revolution integral of a vector field over a closed path. In the case of currents , it is a measure of the vortex strength in the area enclosed by the path.

The term is used in vector analysis , fluid mechanics and electrodynamics . The circulation occurs particularly in Stokes' theorem , which plays a central role in electrodynamics.

Mathematical formulation

If there is  a piece-wise smooth, closed and oriented path in the (this is of particular importance here ) and a vector field that can be integrated along this path, it is called ${\displaystyle W}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle {\vec {v}}}$

${\displaystyle \oint _{W}{\vec {v}}({\vec {r}})\cdot \mathrm {d} {\vec {r}}}$

Circulation  lengthways  ${\displaystyle {\vec {v}}}$ ${\displaystyle W}$ .

If a vector field is  differentiable on an oriented and piecewise smoothly edged surface  , then according to Stokes' theorem the circulation of  along the  corresponding oriented edge is  equal to the surface integral of the rotation of  over  : ${\displaystyle {\vec {v}}}$ ${\displaystyle A}$ ${\displaystyle {\vec {v}}}$ ${\displaystyle A}$ ${\displaystyle \partial A}$ ${\displaystyle {\vec {v}}}$ ${\displaystyle A}$

${\displaystyle \oint _{\partial A}{\vec {v}}\cdot \mathrm {d} {\vec {r}}=\int _{A}\;\operatorname {rot} \;{\vec {v}}\cdot \mathrm {d} {\vec {A}}.}$

The complex circulation

If the vector field lies in a plane, then the properties of complex functions can be used. For this purpose, the vector field is understood as a complex function , the real and imaginary parts of which are the components of the vector field, the plane of which is modeled as a Gaussian number plane , in which the complex number marks a point. The complex circulation is then the complex curve integral of the complex function along a curve in the plane. The real part of the complex circulation is the real circulation along the path introduced above, i.e. the integral over the component of the vector field that is tangential to the curve. The imaginary part, on the other hand, is the integral over the component of the vector field that is perpendicular to the curve. ${\displaystyle w(z)}$ ${\displaystyle z}$ ${\displaystyle w(z)}$ ${\displaystyle W}$ ${\displaystyle W}$

Special rules apply when the complex function is a holomorphic function . If the path includes an area in which the function is holomorphic everywhere, then the complex circulation along the path disappears identically. If there is another curve that includes the path , and the function in the area between the curves and is holomorphic, then the circulation of the function along the curve is equal to its circulation along the curve . ${\displaystyle w(z)}$ ${\displaystyle W}$ ${\displaystyle w(z)}$ ${\displaystyle W}$ ${\displaystyle K}$ ${\displaystyle W}$ ${\displaystyle w(z)}$ ${\displaystyle K}$ ${\displaystyle W}$ ${\displaystyle w(z)}$ ${\displaystyle K}$ ${\displaystyle W}$

These statements are justified in the following.

definition

Be

${\displaystyle w(z):=v_{x}(x,y)-\mathrm {i} \,v_{y}(x,y)\quad {\text{mit}}\quad z=x+\mathrm {i} \,y}$

the complex function with components of the vector field with respect to a Cartesian xy coordinate system in the Gaussian number plane with as an imaginary unit . ${\displaystyle v_{x,y}}$ ${\displaystyle \mathrm {i} }$

The complex circulation of the function along the path ${\displaystyle w}$ ${\displaystyle W}$ is then the complex path integral

${\displaystyle \Gamma _{C}:=\oint _{W}w(z)\,\mathrm {d} z\,.}$

Real and imaginary part of the complex circulation

Arc length representation of curve W with tangent and normal vectors

Inserting the complex function results in the real and the imaginary part:

${\displaystyle {\begin{aligned}\Gamma _{C}&=\oint _{W}w(z)\,\mathrm {d} z=\oint _{W}(v_{x}-\mathrm {i} \,v_{y})(\mathrm {d} x+\mathrm {i} \,\mathrm {d} y)\\&=\oint _{W}(v_{x}\,\mathrm {d} x+v_{y}\,\mathrm {d} y)+\mathrm {i} \oint _{W}(v_{x}\,\mathrm {d} y-v_{y}\,\mathrm {d} x)=:\Gamma +\mathrm {i} \,Q\,.\end{aligned}}}$

The real part

${\displaystyle \Gamma =\oint _{W}(v_{x}\,\mathrm {d} x+v_{y}\,\mathrm {d} y)=\oint _{W}{\vec {v}}\cdot \underbrace {\mathrm {d} {\vec {x}}} _{={\vec {x}}'\,\mathrm {d} s}=\int _{0}^{l}{\vec {v}}\cdot {\vec {x}}'\,\mathrm {d} s}$

is the real circulation introduced above along the path in the plane. The components of the vectors occurring here at right angles to the plane disappear according to the prerequisite: The curve was parameterized above with the arc length so that the length of the curve and the amount of the tangent vector is equal to one, where the line stands for the derivative according to the arc length . ${\displaystyle W}$ ${\displaystyle {\vec {v}}=(v_{x},v_{y},0)\,,\;\mathrm {d} {\vec {x}}=(\mathrm {d} x,\mathrm {d} y,0),\ldots }$ ${\displaystyle W}$ ${\displaystyle W\colon s\in [0,l)\mapsto {\vec {x}}(s)}$ ${\displaystyle s}$ ${\displaystyle l}$ ${\displaystyle {\vec {x}}'}$

The imaginary part of the complex circulation is according to

${\displaystyle Q:=\oint _{W}(v_{x}\,\mathrm {d} y-v_{y}\,\mathrm {d} x)=-\oint _{W}{\vec {v}}\cdot ({\hat {e}}\times \mathrm {d} {\vec {x}})=\int _{0}^{l}{\vec {v}}\cdot ({\vec {x}}'\times {\hat {e}})\,\mathrm {d} s=\int _{0}^{l}{\vec {v}}\cdot {\hat {n}}\,\mathrm {d} s}$

the integral over the components of the vector field normal to the curve. The vector has the magnitude one and is perpendicular to the plane, so that the normal is on the curve, see picture. The arithmetic symbol forms the cross product . ${\displaystyle {\hat {e}}:=(0,0,1)}$ ${\displaystyle {\vec {x}}'\times {\hat {e}}={\hat {n}}}$ ${\displaystyle \times }$

If the function is a complex flow velocity and the path represents a wall around which flow is flowing, then there is no flow through it and the complex circulation of the complex velocity along the contour is real. ${\displaystyle w(z)}$ ${\displaystyle W}$ ${\displaystyle w(z)}$ ${\displaystyle W}$

Circulation of holomorphic functions

The integral set of Cauchy states that the line integral of a complex function between two points is independent of the path when the function holomorphic thus is complex differentiable. The curve integral therefore always disappears along a closed line if the function is holomorphic in the area enclosed by the line. The circulation of a function along a line can therefore only be different from zero if the function cannot be complexly differentiated anywhere within the line.

Integration path that includes the curves W and K.

For the calculation of the circulation it makes no difference whether it is calculated along a path or along another path that encloses the path , as long as the function in the area between the paths and is holomorphic, see picture. If the function in the area shown in yellow is holomorphic, then according to Cauchy's integral theorem: ${\displaystyle W}$ ${\displaystyle K}$ ${\displaystyle W}$ ${\displaystyle K}$ ${\displaystyle W}$ ${\displaystyle w(z)}$

${\displaystyle \int _{W}w(z)\,\mathrm {d} z+\int _{A}w(z)\,\mathrm {d} z-\int _{K}w(z)\,\mathrm {d} z-\int _{B}w(z)\,\mathrm {d} z=0\,.}$

The contributions of the ways and go with the opposite sign, because with them the integration way is opposite to the ways and - as indicated in the picture - runs in opposite directions. Is the line in on, then both their contributions cancel out, the paths and are closed and it is found that the circulation of the function along the path is equal to the along the path is: ${\displaystyle K}$ ${\displaystyle B}$ ${\displaystyle W}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle W}$ ${\displaystyle K}$ ${\displaystyle w(z)}$ ${\displaystyle W}$ ${\displaystyle K}$

${\displaystyle \int _{W}w(z)\,\mathrm {d} z=\int _{K}w(z)\,\mathrm {d} z\,.}$

For example, a circle can be used for the path - as in the figure - if this is more suitable for the calculation. ${\displaystyle K}$

example

Circulation of the magnetic field of a filament

A current filament lying on the axis through which the current flows in the positive direction  is generated by the magnetic field ${\displaystyle z}$ ${\displaystyle z}$ ${\displaystyle I}$

${\displaystyle {\vec {H}}(r,\varphi ,z)={\vec {e}}_{\varphi }{\frac {I}{2\pi r}}}$

surround. The circulation of this vector field along a circle  with  any positive radius  is equal to the current  : ${\displaystyle {\vec {r}}(\varphi )=r{\vec {e}}_{r}(\varphi )}$ ${\displaystyle \varphi \in [0,2\pi )}$ ${\displaystyle r}$ ${\displaystyle I}$

${\displaystyle \oint _{W}{\vec {H}}({\vec {r}})\cdot \mathrm {d} {\vec {r}}=\int _{\varphi =0}^{2\pi }{\vec {e}}_{\varphi }{\frac {I}{2\pi r}}\cdot r{\vec {e}}_{\varphi }\mathrm {d} \varphi =I.}$

This example demonstrates that for the applicability of Stokes' integral theorem, the relevant vector field must be differentiable on a surface bounded by the closed curve. The vector field  from this example is not defined on the -axis. However, the circulation is formed along a circle that encloses the axis. Stokes' integral theorem is not applicable in this case. This is confirmed by the fact that the circulation of  along the circle has a value other than zero  , although the vector field  is rotation-free over its entire domain ( for  ). ${\displaystyle {\vec {H}}}$ ${\displaystyle z}$ ${\displaystyle z}$ ${\displaystyle {\vec {H}}}$ ${\displaystyle I}$ ${\displaystyle {\vec {H}}}$ ${\displaystyle \operatorname {rot} \;{\vec {H}}(r,\varphi ,z)={\vec {0}}}$ ${\displaystyle r>0}$

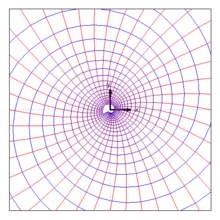
Complex circulation along a circle in a vortex

Streamlines (blue) of a vortex

Be

${\displaystyle w(z)={\frac {Q-\mathrm {i} \,\Gamma }{2\pi z}}}$

the complex velocity field of a vortex with a center at , see the picture and potential flow . The complex circulation of the velocity along a circle with a radius around the origin does not disappear because the velocity at is not complex differentiable and the circle encloses this point. The complex circulation of speed along the way ${\displaystyle z=0}$ ${\displaystyle w(z)}$ ${\displaystyle R}$ ${\displaystyle z=0}$

${\displaystyle W\colon \varphi \in [0,2\pi )\mapsto z(\varphi )=Re^{\mathrm {i} \,\varphi }}$

is calculated by the differential to ${\displaystyle \mathrm {d} z=\mathrm {i} \,Re^{\mathrm {i} \,\varphi }\,\mathrm {d} \varphi }$

${\displaystyle \Gamma _{C}=\oint _{W}w(z)\,\mathrm {d} z=\oint _{0}^{2\pi }{\frac {Q-\mathrm {i} \,\Gamma }{2\pi Re^{\mathrm {i} \,\varphi }}}\,\mathrm {i} \,Re^{\mathrm {i} \,\varphi }\,\mathrm {d} \varphi =\mathrm {i} \,{\frac {Q-\mathrm {i} \,\Gamma }{2\pi }}\oint _{0}^{2\pi }\,\mathrm {d} \varphi =\Gamma +\mathrm {i} \,Q\,.}$

Along the circle, regardless of the selected radius, the speed always has the circulation and the swelling strength , which indicates how large the volume flow passing over the circle is. The complex circulation of speed along the circles is the same for all circles, because the speed in the annulus between any two circles can always be differentiated in a complex manner. ${\displaystyle R}$ ${\displaystyle \Gamma }$ ${\displaystyle Q}$

Here, too, the velocity field outside the origin is free of rotation because the vortex is a potential flow.

literature

• Königsberger: Analysis 2. Springer-Verlag Berlin, 1993. ISBN 3-540-54723-1 .
• Theodore Frankel: The Geometry of Physics (An Introduction). Cambridge University Press, 1997. ISBN 0-521-38753-1 .
• Michael Bestehorn: hydrodynamics and structure formation . Springer, Berlin et al. 2006, ISBN 3-540-33796-2 .