Derivative: Difference between revisions
Manulinho72 (talk | contribs) m forgot to change an r from before, and change some integer to any integer |
Saanidhya B (talk | contribs) m →top: Fixed grammar Tags: canned edit summary Mobile edit Mobile app edit Android app edit |
||
| (1,000 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Instantaneous rate of change (mathematics)}} |
|||
: ''For other senses of this word, see [[derivative (disambiguation)]].'' |
|||
{{other uses|}} |
|||
: ''For a non-technical overview of the subject, see [[Calculus]].'' |
|||
{{pp-semi-indef|small=yes}} |
|||
{{Calculus}} |
|||
{{good article}} |
|||
{{Calculus |differential}} |
|||
The '''derivative''' is a fundamental tool of [[calculus]] that quantifies the sensitivity of change of a [[Function (mathematics)|function]]'s output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the [[slope]] of the [[Tangent|tangent line]] to the [[graph of a function|graph of the function]] at that point. The tangent line is the best [[linear approximation]] of the function near that input value. For this reason, the derivative is often described as the '''instantaneous rate of change''', the ratio of the instantaneous change in the dependent variable to that of the independent variable.{{sfn|Stewart|2002|p=129–130}} The process of finding a derivative is called '''differentiation'''. |
|||
In [[mathematics]], a '''derivative''' is the rate of change of a quantity. A derivative is an ''instantaneous'' rate of change: it is calculated at a specific instant rather than as an average over time. The process of finding a derivative is called differentiation. The reverse process is [[integration (mathematics)|integration]]. The two processes are the central concepts of [[calculus]] and the relationship between them is the [[fundamental theorem of calculus]]. |
|||
There are multiple different notations for differentiation, two of the most commonly used being [[Leibniz notation]] and prime notation. Leibniz notation, named after [[Gottfried Wilhelm Leibniz]], is represented as the ratio of two [[Differential (mathematics)|differentials]], whereas prime notation is written by adding a [[prime mark]]. Higher order notations represent repeated differentiation, and they are usually denoted in Leibniz notation by adding superscripts to the differentials, and in prime notation by adding additional prime marks. The higher order derivatives can be applied in physics; for example, while the first derivative of the position of a moving object with respect to [[time]] is the object's [[velocity]], how the position changes as time advances, the second derivative is the object's [[acceleration]], how the velocity changes as time advances. |
|||
This article assumes an understanding of [[algebra]], [[analytic geometry]], and the [[limit (mathematics)|limit]]. |
|||
Derivatives can be generalized to [[function of several real variables|functions of several real variables]]. In this generalization, the derivative is reinterpreted as a [[linear transformation]] whose graph is (after an appropriate translation) the best linear approximation to the graph of the original function. The [[Jacobian matrix]] is the [[matrix (mathematics)|matrix]] that represents this linear transformation with respect to the basis given by the choice of independent and dependent variables. It can be calculated in terms of the [[partial derivative]]s with respect to the independent variables. For a [[real-valued function]] of several variables, the Jacobian matrix reduces to the [[gradient vector]]. |
|||
For a [[real-valued function]] of a single real variable, the derivative at a point equals the [[slope]] of the line [[tangent#Geometry|tangent]] to the [[graph of a function|graph]] of the function at that point. Derivatives can be used to characterize many properties of a function, including |
|||
*whether and at what rate the function is [[positive relationship|increasing]] or [[inverse relationship|decreasing]] for a fixed value of the input to the function |
|||
*whether and where the function has [[Maxima and minima|maximum or minimum]] values |
|||
==Definition== |
|||
The concept of a derivative can be extended to functions of more than one variable (see [[multivariable calculus]]), to functions of complex variables (see [[complex analysis]]) and to [[derivative (generalizations)|many other cases]]. |
|||
===As a limit=== |
|||
A [[function of a real variable]] <math> f(x) </math> is [[Differentiable function|differentiable]] at a point <math> a </math> of its [[domain of a function|domain]], if its domain contains an [[open interval]] containing <math> a </math>, and the [[limit (mathematics)|limit]] |
|||
<math display="block">L=\lim_{h \to 0}\frac{f(a+h)-f(a)}h </math> |
|||
exists.{{sfnm|1a1=Stewart|1y=2002|1p=127 | 2a1=Strang et al.|2y=2023|2p=[https://openstax.org/books/calculus-volume-1/pages/3-1-defining-the-derivative 220]}} This means that, for every positive [[real number]] <math>\varepsilon</math>, there exists a positive real number <math>\delta</math> such that, for every <math> h </math> such that <math>|h| < \delta</math> and <math>h\ne 0</math> then <math>f(a+h)</math> is defined, and |
|||
<math display="block">\left|L-\frac{f(a+h)-f(a)}h\right|<\varepsilon,</math> |
|||
where the vertical bars denote the [[absolute value]]. This is an example of the [[(ε, δ)-definition of limit]].{{sfn|Gonick|2012|p=83}} |
|||
If the function <math> f </math> is differentiable at <math> a </math>, that is if the limit <math> L </math> exists, then this limit is called the ''derivative'' of <math> f </math> at <math> a </math>. Multiple notations for the derivative exist.{{sfnm|1a1=Gonick|1y=2012|1p=88 | 2a1=Strang et al.|2y=2023|2p=[https://openstax.org/books/calculus-volume-1/pages/3-2-the-derivative-as-a-function 234]}} The derivative of <math> f </math> at <math> a </math> can be denoted <math>f'(a)</math>, read as "<math> f </math> prime of <math> a </math>"; or it can be denoted <math display="inline">\frac{df}{dx}(a)</math>, read as "the derivative of <math> f </math> with respect to <math> x </math> at <math> a </math>" or "<math> df </math> by (or over) <math> dx </math> at <math> a </math>". See {{slink||Notation}} below. If <math> f </math> is a function that has a derivative at every point in its [[domain of a function|domain]], then a function can be defined by mapping every point <math> x </math> to the value of the derivative of <math> f </math> at <math> x </math>. This function is written <math> f' </math> and is called the ''derivative function'' or the ''derivative of'' <math> f </math>. The function <math> f </math> sometimes has a derivative at most, but not all, points of its domain. The function whose value at <math> a </math> equals <math> f'(a) </math> whenever <math> f'(a) </math> is defined and elsewhere is undefined is also called the derivative of <math> f </math>. It is still a function, but its domain may be smaller than the domain of <math> f </math>.{{sfnm |
|||
Differentiation has many applications throughout all numerate disciplines. For example, in [[physics]], the derivative of the position of a moving body is its [[velocity]] and the derivative of the velocity is the [[acceleration]]. |
|||
| 1a1 = Gonick | 1y = 2012 | 1p = 83 |
|||
| 2a1 = Strang et al. | 2y = 2023 | 2p = [https://openstax.org/books/calculus-volume-1/pages/3-2-the-derivative-as-a-function 232] |
|||
}} |
|||
For example, let <math>f</math> be the squaring function: <math>f(x) = x^2</math>. Then the quotient in the definition of the derivative is{{sfn|Gonick|2012|pp=77–80}} |
|||
==History of differentiation == |
|||
<math display="block">\frac{f(a+h) - f(a)}{h} = \frac{(a+h)^2 - a^2}{h} = \frac{a^2 + 2ah + h^2 - a^2}{h} = 2a + h.</math> |
|||
{{main|History of calculus}} |
|||
The division in the last step is valid as long as <math>h \neq 0</math>. The closer <math>h</math> is to <math>0</math>, the closer this expression becomes to the value <math>2a</math>. The limit exists, and for every input <math>a</math> the limit is <math>2a</math>. So, the derivative of the squaring function is the doubling function: <math>f'(x) = 2x</math>. |
|||
The modern development of calculus is credited to [[Isaac Newton]] and [[Gottfried Leibniz]] who worked independently in the late [[1600s]].<ref>{{cite book|last=Gribbin|first=John|title=Science a History|publisher=Penguin books|year=2002|pages=180-181}}</ref> |
|||
Newton began his work in 1666 and Leibniz began his in 1676. However, Leibniz published his first paper in 1684, predating Newton's publication in 1693. There was a bitter [[Newton v. Leibniz calculus controversy|controversy]] between the two men over who first invented calculus which shook the mathematical community in the early 18th century. Both Newton and Leibniz based their work on that of earlier mathematicians. [[Isaac Barrow]] (1630 - 1677) is often credited with the early development of what is now called the derivative. <ref> Howard Eves, ''An Introduction to the History of Mathematics'', Saunders, 1990, ISBN 0-03-029558-0 </ref> |
|||
{{multiple image |
|||
== Differentiation and differentiability == |
|||
| total_width = 480 |
|||
| image1 = Tangent to a curve.svg |
|||
| caption1 = The [[graph of a function]], drawn in black, and a [[tangent line]] to that graph, drawn in red. The [[slope]] of the tangent line is equal to the derivative of the function at the marked point. |
|||
| image2 = Tangent function animation.gif |
|||
| caption2 = The derivative at different points of a differentiable function. In this case, the derivative is equal to <math>\sin \left(x^2\right) + 2x^2 \cos\left(x^2\right)</math> |
|||
}} |
|||
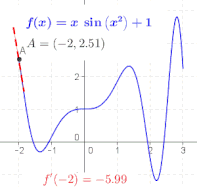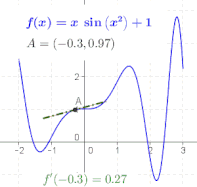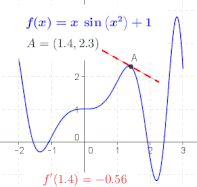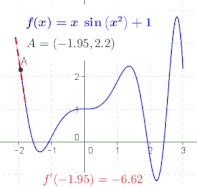
The ratio in the definition of the derivative is the slope of the line through two points on the graph of the function <math>f</math>, specifically the points <math>(a,f(a))</math> and <math>(a+h, f(a+h))</math>. As <math>h</math> is made smaller, these points grow closer together, and the slope of this line approaches the limiting value, the slope of the [[tangent]] to the graph of <math>f</math> at <math>a</math>. In other words, the derivative is the slope of the tangent.{{sfnm |
|||
| 1a1 = Thompson | 1y = 1998 | 1pp = 34,104 |
|||
| 2a1 = Stewart | 2y = 2002 | 2p = 128 |
|||
}} |
|||
===Using infinitesimals=== |
|||
'''Differentiation''' expresses the rate at which a quantity, ''y'', changes with respect to the change in another quantity, ''x'', on which it has a [[function (mathematics)|functional relationship]]. Using the symbol Δ ([[Delta (letter)|Delta]]) to refer to change in a quantity, this rate is defined as a [[limit of a function|limit]] of difference quotients |
|||
One way to think of the derivative <math display="inline">\frac{df}{dx}(a)</math> is as the ratio of an [[infinitesimal]] change in the output of the function <math>f</math> to an infinitesimal change in its input.{{sfn|Thompson|1998|pp=84–85}} In order to make this intuition rigorous, a system of rules for manipulating infinitesimal quantities is required.{{sfn|Keisler|2012|pp=902–904}} The system of [[hyperreal number]]s is a way of treating [[Infinity|infinite]] and infinitesimal quantities. The hyperreals are an [[Field extension|extension]] of the [[real number]]s that contain numbers greater than anything of the form <math>1 + 1 + \cdots + 1 </math> for any finite number of terms. Such numbers are infinite, and their [[Multiplicative inverse|reciprocal]]s are infinitesimals. The application of hyperreal numbers to the foundations of calculus is called [[nonstandard analysis]]. This provides a way to define the basic concepts of calculus such as the derivative and integral in terms of infinitesimals, thereby giving a precise meaning to the <math>d</math> in the Leibniz notation. Thus, the derivative of <math>f(x)</math> becomes <math display="block">f'(x) = \operatorname{st}\left( \frac{f(x + dx) - f(x)}{dx} \right)</math> for an arbitrary infinitesimal <math>dx</math>, where <math>\operatorname{st}</math> denotes the [[standard part function]], which "rounds off" each finite hyperreal to the nearest real.{{sfnm |
|||
| 1a1 = Keisler | 1y = 2012 | 1p = 45 |
|||
| 2a1 = Henle | 2a2 = Kleinberg | 2y = 2003 | 2p = 66 |
|||
}} Taking the squaring function <math>f(x) = x^2</math> as an example again, |
|||
<math display="block"> \begin{align} |
|||
f'(x) &= \operatorname{st}\left(\frac{x^2 + 2x \cdot dx + (dx)^2 -x^2}{dx}\right) \\ |
|||
&= \operatorname{st}\left(\frac{2x \cdot dx + (dx)^2}{dx}\right) \\ |
|||
&= \operatorname{st}\left(\frac{2x \cdot dx}{dx} + \frac{(dx)^2}{dx}\right) \\ |
|||
&= \operatorname{st}\left(2x + dx\right) \\ |
|||
&= 2x. |
|||
\end{align} </math> |
|||
==Continuity and differentiability== |
|||
: <math> \lim_{{\Delta x} \to 0}\frac{\Delta y}{\Delta x} </math> |
|||
{{multiple image |
|||
| total_width = 480 |
|||
| image1 = Right-continuous.svg |
|||
| caption1 = This function does not have a derivative at the marked point, as the function is not continuous there (specifically, it has a [[jump discontinuity]]). |
|||
| image2 = Absolute value.svg |
|||
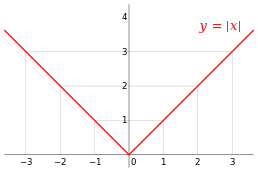
| caption2 = The absolute value function is continuous but fails to be differentiable at {{math|''x'' {{=}} 0}} since the tangent slopes do not approach the same value from the left as they do from the right. |
|||
}} |
|||
If <math> f </math> is [[differentiable]] at <math> a </math>, then <math> f </math> must also be [[continuous function|continuous]] at <math> a </math>.{{sfn|Gonick|2012|p=156}} As an example, choose a point <math> a </math> and let <math> f </math> be the [[step function]] that returns the value 1 for all <math> x </math> less than <math> a </math>, and returns a different value 10 for all <math> x </math> greater than or equal to <math> a </math>. The function <math> f </math> cannot have a derivative at <math> a </math>. If <math> h </math> is negative, then <math> a + h </math> is on the low part of the step, so the secant line from <math> a </math> to <math> a + h </math> is very steep; as <math> h </math> tends to zero, the slope tends to infinity. If <math> h </math> is positive, then <math> a + h </math> is on the high part of the step, so the secant line from <math> a </math> to <math> a + h </math> has slope zero. Consequently, the secant lines do not approach any single slope, so the limit of the difference quotient does not exist. However, even if a function is continuous at a point, it may not be differentiable there. For example, the [[absolute value]] function given by <math> f(x) = |x| </math> is continuous at <math> x = 0 </math>, but it is not differentiable there. If <math> h </math> is positive, then the slope of the secant line from 0 to <math> h </math> is one; if <math> h </math> is negative, then the slope of the secant line from <math> 0 </math> to <math> h </math> is <math> -1 </math>.{{sfn|Gonick|2012|p=149}} This can be seen graphically as a "kink" or a "cusp" in the graph at <math>x=0</math>. Even a function with a smooth graph is not differentiable at a point where its [[Vertical tangent|tangent is vertical]]: For instance, the function given by <math> f(x) = x^{1/3} </math> is not differentiable at <math> x = 0 </math>. In summary, a function that has a derivative is continuous, but there are continuous functions that do not have a derivative.{{sfn|Gonick|2012|p=156}} |
|||
Most functions that occur in practice have derivatives at all points or [[Almost everywhere|almost every]] point. Early in the [[history of calculus]], many mathematicians assumed that a continuous function was differentiable at most points.{{sfnm |
|||
which means the limit as <math>\Delta x</math> approaches 0. In [[Leibniz notation|Leibniz's notation for derivatives]], the derivative of ''y'' with respect to ''x'' is written |
|||
| 1a1 = Jašek | 1y = 1922 |
|||
| 2a1 = Jarník | 2y = 1922 |
|||
| 3a1 = Rychlík | 3y = 1923 |
|||
}} Under mild conditions (for example, if the function is a [[monotone function|monotone]] or a [[Lipschitz function]]), this is true. However, in 1872, Weierstrass found the first example of a function that is continuous everywhere but differentiable nowhere. This example is now known as the [[Weierstrass function]].{{sfn|David|2018}} In 1931, [[Stefan Banach]] proved that the set of functions that have a derivative at some point is a [[meager set]] in the space of all continuous functions. Informally, this means that hardly any random continuous functions have a derivative at even one point.<ref>{{harvnb|Banach|1931}}, cited in {{harvnb|Hewitt|Stromberg|1965}}.</ref> |
|||
== Notation == |
|||
: <math> \frac{dy}{dx} \,\!</math> |
|||
{{Main|Notation for differentiation}} |
|||
One common symbol for the derivative of a function is [[Leibniz notation]]. They are written as the quotient of two [[differential (mathematics)|differentials]] <math> dy </math> and <math> dx </math>,{{sfn|Apostol|1967|p=172}} which were introduced by [[Gottfried Leibniz|Gottfried Wilhelm Leibniz]] in 1675.{{sfn|Cajori|2007|p=204}} It is still commonly used when the equation <math>y=f(x)</math> is viewed as a functional relationship between [[dependent and independent variables]]. The first derivative is denoted by <math display="inline">\frac{dy}{dx} </math>, read as "the derivative of <math> y </math> with respect to <math> x </math>".{{sfn|Moore|Siegel|2013|p=110}} This derivative can alternately be treated as the application of a [[differential operator]] to a function, <math display="inline">\frac{dy}{dx} = \frac{d}{dx} f(x).</math> Higher derivatives are expressed using the notation <math display="inline"> \frac{d^n y}{dx^n} </math> for the <math>n</math>-th derivative of <math>y = f(x)</math>. These are abbreviations for multiple applications of the derivative operator; for example, <math display="inline">\frac{d^2y}{dx^2} = \frac{d}{dx}\Bigl(\frac{d}{dx} f(x)\Bigr).</math>{{sfn|Varberg|Purcell|Rigdon|2007|p=125–126}} Unlike some alternatives, Leibniz notation involves explicit specification of the variable for differentiation, in the denominator, which removes ambiguity when working with multiple interrelated quantities. The derivative of a [[function composition|composed function]] can be expressed using the [[chain rule]]: if <math>u = g(x)</math> and <math>y = f(g(x))</math> then <math display="inline">\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}.</math><ref>In the formulation of calculus in terms of limits, various authors have assigned the <math> du </math> symbol various meanings. Some authors such as {{harvnb|Varberg|Purcell|Rigdon|2007}}, p. 119 and {{harvnb|Stewart|2002}}, p. 177 do not assign a meaning to <math> du </math> by itself, but only as part of the symbol <math display="inline"> \frac{du}{dx} </math>. Others define <math> dx </math> as an independent variable, and define <math> du </math> by <math display="block"> du = dx f'(x). </math> |
|||
In [[non-standard analysis]] <math> du </math> is defined as an infinitesimal. It is also interpreted as the [[exterior derivative]] of a function <math> u </math>. See [[differential (infinitesimal)]] for further information.</ref> |
|||
Another common notation for differentiation is by using the [[Prime (symbol)|prime mark]] in the symbol of a function <math> f(x) </math>. This is known as ''prime notation'', due to [[Joseph-Louis Lagrange]].{{sfn|Schwartzman|1994|p=[https://books.google.com/books?id=PsH2DwAAQBAJ&pg=PA171 171]}} The first derivative is written as <math> f'(x) </math>, read as "<math> f </math> prime of <math> x </math>", or <math> y' </math>, read as "<math> y </math> prime".{{sfnm |
|||
suggesting the ratio of two [[infinitesimal]] quantities. The above expression is pronounced in various ways such as "d y by d x" or "d y over d x". The oral form "d y d x" is often used conversationally, although it may lead to confusion. |
|||
| 1a1 = Moore | 1a2 = Siegel | 1y = 2013 | 1p = 110 |
|||
| 2a1 = Goodman | 2y = 1963 | 2p = 78–79 |
|||
}} Similarly, the second and the third derivatives can be written as <math> f'' </math> and <math> f''' </math>, respectively.{{sfnm |
|||
| 1a1 = Varberg | 1a2 = Purcell | 1a3 = Rigdon | 1y = 2007 | 1p = 125–126 |
|||
| 2a1 = Cajori | 2y = 2007 | 2p = 228 |
|||
}} For denoting the number of higher derivatives beyond this point, some authors use Roman numerals in [[Subscript and superscript|superscript]], whereas others place the number in parentheses, such as <math>f^{\mathrm{iv}}</math> or <math> f^{(4)}.</math>{{sfnm |
|||
| 1a1 = Choudary | 1a2 = Niculescu | 1y = 2014 | 1p = [https://books.google.com/books?id=I8aPBQAAQBAJ&pg=PA222 222] |
|||
| 2a1 = Apostol | 2y = 1967 | 2p = 171 |
|||
}} The latter notation generalizes to yield the notation <math>f^{(n)}</math> for the {{nowrap|1=<math>n</math>-}}th derivative of <math>f</math>.{{sfn|Varberg|Purcell|Rigdon|2007|p=125–126}} |
|||
In [[Newton's notation]] or the ''dot notation,'' a dot is placed over a symbol to represent a time derivative. If <math> y </math> is a function of <math> t </math>, then the first and second derivatives can be written as <math>\dot{y}</math> and <math>\ddot{y}</math>, respectively. This notation is used exclusively for derivatives with respect to time or [[arc length]]. It is typically used in [[differential equation]]s in [[physics]] and [[differential geometry]].{{sfnm |
|||
Modern mathematicians do not bother with "dependent quantities", but simply state that differentiation is a mathematical [[operator|operation]] on functions. One precise way to define the derivative is as a [[Limit (mathematics)|limit]] <ref>Spivak, ch 10</ref>: |
|||
| 1a1 = Evans | 1y = 1999 | 1p = 63 |
|||
| 2a1 = Kreyszig | 2y = 1991 | 2p = 1 |
|||
}} However, the dot notation becomes unmanageable for high-order derivatives (of order 4 or more) and cannot deal with multiple independent variables. |
|||
Another notation is ''D-notation'', which represents the differential operator by the symbol <math>D.</math>{{sfn|Varberg|Purcell|Rigdon|2007|p=125–126}} The first derivative is written <math>D f(x)</math> and higher derivatives are written with a superscript, so the <math>n</math>-th derivative is <math>D^nf(x).</math> This notation is sometimes called ''Euler notation'', although it seems that [[Leonhard Euler]] did not use it, and the notation was introduced by [[Louis François Antoine Arbogast]].{{sfn|Cajori|1923}} To indicate a partial derivative, the variable differentiated by is indicated with a subscript, for example given the function <math>u = f(x, y),</math> its partial derivative with respect to <math>x</math> can be written <math>D_x u</math> or <math>D_x f(x,y).</math> Higher partial derivatives can be indicated by superscripts or multiple subscripts, e.g. <math display=inline>D_{xy} f(x,y) = \frac{\partial}{\partial y} \Bigl(\frac{\partial}{\partial x} f(x,y) \Bigr)</math> and <math display=inline>D_{x}^2 f(x,y) = \frac{\partial}{\partial x} \Bigl(\frac{\partial}{\partial x} f(x,y) \Bigr)</math>.{{sfnm |
|||
: <math>\lim_{h \to 0}\frac{f(x+h) - f(x)}{h}.</math> |
|||
| 1a1 = Apostol | 1y = 1967 | 1p = 172 |
|||
| 2a1 = Varberg | 2a2 = Purcell | 2a3 = Rigdon | 2y = 2007 | 2p = 125–126 |
|||
}} |
|||
==Rules of computation== |
|||
A function is '''differentiable''' at a point ''x'' if the above limit exists (as a finite real number) at that point. A function is differentiable on an [[Interval (mathematics)|interval]] if it is differentiable at every point within the interval. |
|||
{{Main|Differentiation rules}} |
|||
In principle, the derivative of a function can be computed from the definition by considering the difference quotient and computing its limit. Once the derivatives of a few simple functions are known, the derivatives of other functions are more easily computed using ''rules'' for obtaining derivatives of more complicated functions from simpler ones. This process of finding a derivative is known as '''differentiation'''.{{sfn|Apostol|1967|p=160}} |
|||
===Rules for basic functions=== |
|||
As an alternative, the development of [[nonstandard analysis]] in the 20th century showed that Leibniz's original idea of the derivative as a ratio of infinitesimals can be made as rigorous as the formulation in terms of limits. |
|||
The following are the rules for the derivatives of the most common basic functions. Here, <math> a </math> is a real number, and <math> e </math> is [[e (mathematical constant)|the mathematical constant approximately {{nowrap|1=2.71828}}]].<ref>{{harvnb|Varberg|Purcell|Rigdon|2007}}. See p. 133 for the power rule, p. 115–116 for the trigonometric functions, p. 326 for the natural logarithm, p. 338–339 for exponential with base <math> e </math>, p. 343 for the exponential with base <math> a </math>, p. 344 for the logarithm with base <math> a </math>, and p. 369 for the inverse of trigonometric functions.</ref> |
|||
* ''[[Power rule|Derivatives of powers]]'': |
|||
If a function is not [[Continuous function|continuous]] at a point, then there is no tangent line and the function is not differentiable at that point. However, even if a function is continuous at a point, it may not be differentiable there. For example, the function ''y'' = |''x''| is continuous at ''x'' = 0, but it is not differentiable there, due to the fact that the limit in the above definition does not exist (the limit from the right is 1 while the limit from the left is −1). Graphically, we see this as a "kink" in the graph at ''x'' = 0. Even a function with a smooth graph is not differentiable at a point where its tangent is vertical, such as ''x'' = 0 for <math>y = \sqrt[3]{x}</math>. Thus, differentiability implies continuity, but not vice versa. One famous example of a function that is continuous everywhere but differentiable nowhere is the [[Weierstrass function]]. |
|||
*: <math> \frac{d}{dx}x^a = ax^{a-1} </math> |
|||
<!--DO NOT ADD TO THIS LIST--> |
|||
* ''Functions of [[Exponential function|exponential]], [[natural logarithm]], and [[logarithm]] with general base'': |
|||
*: <math> \frac{d}{dx}e^x = e^x </math> |
|||
*: <math> \frac{d}{dx}a^x = a^x\ln(a) </math>, for <math> a > 0 </math> |
|||
*: <math> \frac{d}{dx}\ln(x) = \frac{1}{x} </math>, for <math> x > 0 </math> |
|||
*: <math> \frac{d}{dx}\log_a(x) = \frac{1}{x\ln(a)} </math>, for <math> x, a > 0 </math> |
|||
<!--DO NOT ADD TO THIS LIST--> |
|||
* ''[[Trigonometric functions]]'': |
|||
*: <math> \frac{d}{dx}\sin(x) = \cos(x) </math> |
|||
*: <math> \frac{d}{dx}\cos(x) = -\sin(x) </math> |
|||
*: <math> \frac{d}{dx}\tan(x) = \sec^2(x) = \frac{1}{\cos^2(x)} = 1 + \tan^2(x) </math> |
|||
<!--DO NOT ADD TO THIS LIST--> |
|||
* ''[[Inverse trigonometric functions]]'': |
|||
*: <math> \frac{d}{dx}\arcsin(x) = \frac{1}{\sqrt{1-x^2}} </math>, for <math> -1 < x < 1 </math> |
|||
*: <math> \frac{d}{dx}\arccos(x)= -\frac{1}{\sqrt{1-x^2}} </math>, for <math> -1 < x < 1 </math> |
|||
*: <math> \frac{d}{dx}\arctan(x)= \frac{1}{{1+x^2}} </math> |
|||
<!--DO NOT ADD TO THIS LIST--> |
|||
==={{anchor|Rules}}Rules for combined functions=== |
|||
The derivative of a function ''f'' at ''x'' is a quantity which varies if ''x'' varies. The derivative is therefore itself a function of ''x''; there are several notations for this function, but ''f'' ' is common. |
|||
Given that the <math> f </math> and <math> g </math> are the functions. The following are some of the most basic rules for deducing the derivative of functions from derivatives of basic functions.<ref> For constant rule and sum rule, see {{harvnb|Apostol|1967|p=161, 164}}, respectively. For the product rule, quotient rule, and chain rule, see {{harvnb|Varberg|Purcell|Rigdon|2007|p=111–112, 119}}, respectively. For the special case of the product rule, that is, the product of a constant and a function, see {{harvnb|Varberg|Purcell|Rigdon|2007|p=108–109}}.</ref> |
|||
* ''Constant rule'': if <math>f</math> is constant, then for all <math>x</math>, |
|||
*: <math>f'(x) = 0. </math> |
|||
* ''[[Linearity of differentiation|Sum rule]]'': |
|||
*: <math>(\alpha f + \beta g)' = \alpha f' + \beta g' </math> for all functions <math>f</math> and <math>g</math> and all real numbers ''<math>\alpha</math>'' and ''<math>\beta</math>''. |
|||
* ''[[Product rule]]'': |
|||
*: <math>(fg)' = f 'g + fg' </math> for all functions <math>f</math> and <math>g</math>. As a special case, this rule includes the fact <math>(\alpha f)' = \alpha f'</math> whenever <math>\alpha</math> is a constant because <math>\alpha' f = 0 \cdot f = 0</math> by the constant rule. |
|||
* ''[[Quotient rule]]'': |
|||
*: <math>\left(\frac{f}{g} \right)' = \frac{f'g - fg'}{g^2}</math> for all functions <math>f</math> and <math>g</math> at all inputs where {{nowrap|''g'' ≠ 0}}. |
|||
* ''[[Chain rule]]'' for [[Function composition|composite functions]]: If <math>f(x) = h(g(x))</math>, then |
|||
*: <math>f'(x) = h'(g(x)) \cdot g'(x). </math> |
|||
=== Computation example === |
|||
The derivative of a derivative, if it exists, is called a '''second derivative'''. Similarly, the derivative of a second derivative is a '''third derivative''', and so on. At a given point or on a given interval, a function may have no derivative, a finite number of successive derivatives, or an infinite number of successive derivatives. On the real line, every polynomial function is infinitely differentiable, meaning that the derivative can be taken at any point, successively, any number of times. After a finite number of differentiations, the function ''f''(''x'') = 0 is reached, and all subsequent derivatives are 0. |
|||
The derivative of the function given by <math>f(x) = x^4 + \sin \left(x^2\right) - \ln(x) e^x + 7</math> is |
|||
<math display="block"> \begin{align} |
|||
f'(x) &= 4 x^{(4-1)}+ \frac{d\left(x^2\right)}{dx}\cos \left(x^2\right) - \frac{d\left(\ln {x}\right)}{dx} e^x - \ln(x) \frac{d\left(e^x\right)}{dx} + 0 \\ |
|||
&= 4x^3 + 2x\cos \left(x^2\right) - \frac{1}{x} e^x - \ln(x) e^x. |
|||
\end{align} </math> |
|||
Here the second term was computed using the [[chain rule]] and the third term using the [[product rule]]. The known derivatives of the elementary functions <math> x^2 </math>, <math> x^4 </math>, <math> \sin (x) </math>, <math> \ln (x) </math>, and <math> \exp(x) = e^x </math>, as well as the constant <math> 7 </math>, were also used. |
|||
== Higher-order derivatives{{anchor|order of derivation|Order}} == |
|||
== Newton's difference quotient == |
|||
''Higher order derivatives'' means that a function is differentiated repeatedly. Given that <math> f </math> is a differentiable function, the derivative of <math> f </math> is the first derivative, denoted as <math> f' </math>. The derivative of <math> f' </math> is the [[second derivative]], denoted as <math> f'' </math>, and the derivative of <math> f'' </math> is the [[third derivative]], denoted as <math> f''' </math>. By continuing this process, if it exists, the {{nowrap|1=<math> n </math>-}}th derivative as the derivative of the {{nowrap|1=<math> (n - 1) </math>-}}th derivative or the ''derivative of order <math> n </math>''. As has been [[#Notation|discussed above]], the generalization of derivative of a function <math> f </math> may be denoted as <math> f^{(n)} </math>.{{sfnm |
|||
[[Image:Tangent-calculus.png|thumb|300px|Tangent line at (''x'', ''f''(''x''))]] |
|||
| 1a1 = Apostol | 1y = 1967 | 1p = 160 |
|||
| 2a1 = Varberg | 2a2 = Purcell | 2a3 = Rigdon | 2y = 2007 | 2p = 125–126 |
|||
}} A function that has <math> k </math> successive derivatives is called ''<math> k </math> times differentiable''. If the {{nowrap|1=<math> k </math>-}}th derivative is continuous, then the function is said to be of [[differentiability class]] <math> C^k </math>.{{sfn|Warner|1983|p=5}} A function that has infinitely many derivatives is called ''infinitely differentiable'' or ''[[smoothness|smooth]]''.{{sfn|Debnath|Shah|2015|p=[https://books.google.com/books?id=qPuWBQAAQBAJ&pg=PA40 40]}} One example of the infinitely differentiable function is [[polynomial]]; differentiate this function repeatedly results the [[constant function]], and the infinitely subsequent derivative of that function are all zero.{{sfn|Carothers|2000|p=[https://books.google.com/books?id=4VFDVy1NFiAC&pg=PA176 176]}} |
|||
{{anchor|1=Instantaneous rate of change}}In [[Differential calculus#Applications of derivatives|one of its applications]], the higher-order derivatives may have specific interpretations in [[physics]]. Suppose that a function represents the position of an object at the time. The first derivative of that function is the [[velocity]] of an object with respect to time, the second derivative of the function is the [[acceleration]] of an object with respect to time,{{sfn|Apostol|1967|p=160}} and the third derivative is the [[jerk (physics)|jerk]].{{sfn|Stewart|2002|p=193}} |
|||
[[Image:Secant-calculus.png|thumb|300px|Secant to curve ''y''= ''f''(''x'') determined by points (''x'', ''f''(''x'')) and (''x''+''h'', ''f''(''x''+''h'')).]] |
|||
[[Image:Lim-secant.png|thumb|300px|Tangent line as limit of secants.]] |
|||
The derivative of a function ''f'' at ''x'' is geometrically the slope of the tangent line to the graph of ''f'' at ''x''. The slope of the tangent line is a limit, the limit of the slopes of the secant lines between two points on a curve, as the distance between the two points goes to zero. |
|||
==In other dimensions== |
|||
{{See also|Vector calculus|Multivariable calculus}} |
|||
===Vector-valued functions=== |
|||
To find the slopes of the nearby secant lines, we represent the horizontal distance between two points by a symbol ''h'', which can be either positive or negative, depending on whether the second point is to the right or the left of the first. The slope of the line through the points (''x'',''f(x)'') and (''x+h'',''f(x+h)'') is |
|||
A [[vector-valued function]] <math> \mathbf{y} </math> of a real variable sends real numbers to vectors in some [[vector space]] <math> \R^n </math>. A vector-valued function can be split up into its coordinate functions <math> y_1(t), y_2(t), \dots, y_n(t) </math>, meaning that <math> \mathbf{y} = (y_1(t), y_2(t), \dots, y_n(t))</math>. This includes, for example, [[parametric curve]]s in <math> \R^2 </math> or <math> \R^3 </math>. The coordinate functions are real-valued functions, so the above definition of derivative applies to them. The derivative of <math> \mathbf{y}(t) </math> is defined to be the [[Vector (geometric)|vector]], called the [[Differential geometry of curves|tangent vector]], whose coordinates are the derivatives of the coordinate functions. That is,{{sfn|Stewart|2002|p=893}} |
|||
<math display="block"> \mathbf{y}'(t)=\lim_{h\to 0}\frac{\mathbf{y}(t+h) - \mathbf{y}(t)}{h}, </math> |
|||
if the limit exists. The subtraction in the numerator is the subtraction of vectors, not scalars. If the derivative of <math> \mathbf{y} </math> exists for every value of <math> t </math>, then <math> \mathbf{y} </math> is another vector-valued function.{{sfn|Stewart|2002|p=893}} |
|||
===Partial derivatives=== |
|||
: <math>{f(x+h)-f(x)\over h}.</math> |
|||
{{Main|Partial derivative}} |
|||
Functions can depend upon [[function (mathematics)#Multivariate function|more than one variable]]. A [[partial derivative]] of a function of several variables is its derivative with respect to one of those variables, with the others held constant. Partial derivatives are used in [[vector calculus]] and [[differential geometry]]. As with ordinary derivatives, multiple notations exist: the partial derivative of a function <math>f(x, y, \dots)</math> with respect to the variable <math>x</math> is variously denoted by |
|||
{{block indent | em = 1.2 | text = <math>f_x</math>, <math>f'_x</math>, <math>\partial_x f</math>, <math>\frac{\partial}{\partial x}f</math>, or <math>\frac{\partial f}{\partial x}</math>,}} |
|||
among other possibilities.{{sfnm |
|||
| 1a1 = Stewart | 1y = 2002 | 1p = [https://archive.org/details/calculus0000stew/page/947/mode/1up 947] |
|||
| 2a1 = Christopher | 2y = 2013 | 2p = 682 |
|||
}} It can be thought of as the rate of change of the function in the <math>x</math>-direction.{{sfn|Stewart|2002|p=[https://archive.org/details/calculus0000stew/page/949 949]}} Here [[∂]] is a rounded ''d'' called the '''partial derivative symbol'''. To distinguish it from the letter ''d'', ∂ is sometimes pronounced "der", "del", or "partial" instead of "dee".{{sfnm |
|||
| 1a1 = Silverman | 1y = 1989 | 1p = [https://books.google.com/books?id=CQ-kqE9Yo9YC&pg=PA216 216] |
|||
| 2a1 = Bhardwaj | 2y= 2005 | 2loc = See [https://books.google.com/books?id=qSlGMwpNueoC&pg=SA6-PA4 p. 6.4] |
|||
}} For example, let <math>f(x,y) = x^2 + xy + y^2</math>, then the partial derivative of function <math> f </math> with respect to both variables <math> x </math> and <math> y </math> are, respectively: |
|||
<math display="block"> \frac{\partial f}{\partial x} = 2x + y, \qquad \frac{\partial f}{\partial y} = x + 2y.</math> |
|||
In general, the partial derivative of a function <math> f(x_1, \dots, x_n) </math> in the direction <math> x_i </math> at the point <math>(a_1, \dots, a_n) </math> is defined to be:{{sfn|Mathai|Haubold|2017|p=[https://books.google.com/books?id=v20uDwAAQBAJ&pg=PA52 52]}} |
|||
<math display="block">\frac{\partial f}{\partial x_i}(a_1,\ldots,a_n) = \lim_{h \to 0}\frac{f(a_1,\ldots,a_i+h,\ldots,a_n) - f(a_1,\ldots,a_i,\ldots,a_n)}{h}.</math> |
|||
This is fundamental for the study of the [[functions of several real variables]]. Let <math> f(x_1, \dots, x_n) </math> be such a [[real-valued function]]. If all partial derivatives <math> f </math> with respect to <math> x_j </math> are defined at the point <math> (a_1, \dots, a_n) </math>, these partial derivatives define the vector |
|||
This expression is [[Isaac Newton|Newton]]'s '''[[difference quotient]]'''. The '''derivative of''' '''''f''''' '''at''' '''''x''''' is the limit of the value of the difference quotient as the secant lines get closer and closer to the tangent line: |
|||
<math display="block">\nabla f(a_1, \ldots, a_n) = \left(\frac{\partial f}{\partial x_1}(a_1, \ldots, a_n), \ldots, \frac{\partial f}{\partial x_n}(a_1, \ldots, a_n)\right),</math> |
|||
which is called the [[gradient]] of <math> f </math> at <math> a </math>. If <math> f </math> is differentiable at every point in some domain, then the gradient is a [[vector-valued function]] <math> \nabla f </math> that maps the point <math> (a_1, \dots, a_n) </math> to the vector <math> \nabla f(a_1, \dots, a_n) </math>. Consequently, the gradient determines a [[vector field]].{{sfn|Gbur|2011|pp=36–37}} |
|||
===Directional derivatives=== |
|||
: <math>f'(x)=\lim_{h\to 0}{f(x+h)-f(x)\over h}.</math> |
|||
{{Main|Directional derivative}} |
|||
If <math> f </math> is a real-valued function on <math> \R^n </math>, then the partial derivatives of <math> f </math> measure its variation in the direction of the coordinate axes. For example, if <math> f </math> is a function of <math> x </math> and <math> y </math>, then its partial derivatives measure the variation in <math> f </math> in the <math> x </math> and <math> y </math> direction. However, they do not directly measure the variation of <math> f </math> in any other direction, such as along the diagonal line <math> y = x </math>. These are measured using directional derivatives. Choose a vector <math> \mathbf{v} = (v_1,\ldots,v_n) </math>, then the [[directional derivative]] of <math> f </math> in the direction of <math> \mathbf{v} </math> at the point <math> \mathbf{x} </math> is:{{sfn|Varberg|Purcell|Rigdon|2007|p=642}} |
|||
<math display="block"> D_{\mathbf{v}}{f}(\mathbf{x}) = \lim_{h \rightarrow 0}{\frac{f(\mathbf{x} + h\mathbf{v}) - f(\mathbf{x})}{h}}.</math> |
|||
<!--In some cases, it may be easier to compute or estimate the directional derivative after changing the length of the vector. Often this is done to turn the problem into the computation of a directional derivative in the direction of a unit vector. To see how this works, suppose that {{nowrap|1='''v''' = ''λ'''''u'''}} where '''u''' is a unit vector in the direction of '''v'''. Substitute {{nowrap|1=''h'' = ''k''/''λ''}} into the difference quotient. The difference quotient becomes: |
|||
:<math>\frac{f(\mathbf{x} + (k/\lambda)(\lambda\mathbf{u})) - f(\mathbf{x})}{k/\lambda} |
|||
= \lambda\cdot\frac{f(\mathbf{x} + k\mathbf{u}) - f(\mathbf{x})}{k}.</math> |
|||
This is ''λ'' times the difference quotient for the directional derivative of ''f'' with respect to '''u'''. Furthermore, taking the limit as ''h'' tends to zero is the same as taking the limit as ''k'' tends to zero because ''h'' and ''k'' are multiples of each other. Therefore, {{nowrap|1=''D''<sub>'''v'''</sub>(''f'') = λ''D''<sub>'''u'''</sub>(''f'')}}. Because of this rescaling property, directional derivatives are frequently considered only for unit vectors.--> |
|||
If all the partial derivatives of <math> f </math> exist and are continuous at <math> \mathbf{x} </math>, then they determine the directional derivative of <math> f </math> in the direction <math> \mathbf{v} </math> by the formula:{{sfn|Guzman|2003|p=[https://books.google.com/books?id=aI_qBwAAQBAJ&pg=PA35 35]}} |
|||
<math display="block"> D_{\mathbf{v}}{f}(\mathbf{x}) = \sum_{j=1}^n v_j \frac{\partial f}{\partial x_j}. </math> |
|||
===Total derivative, total differential and Jacobian matrix=== |
|||
If the derivative of ''f'' exists at every point ''x'' in the domain, we can define the '''derivative of''' '''''f''''' to be the function whose value at a point ''x'' is the derivative of ''f'' at ''x''. |
|||
{{Main|Total derivative}} |
|||
When <math> f </math> is a function from an open subset of <math> \R^n </math> to <math> \R^m </math>, then the directional derivative of <math> f </math> in a chosen direction is the best linear approximation to <math> f </math> at that point and in that direction. However, when <math> n > 1 </math>, no single directional derivative can give a complete picture of the behavior of <math> f </math>. The total derivative gives a complete picture by considering all directions at once. That is, for any vector <math> \mathbf{v} </math> starting at <math> \mathbf{a} </math>, the linear approximation formula holds:{{sfn|Davvaz|2023|p=[https://books.google.com/books?id=ofzKEAAAQBAJ&pg=PA266 266]}} |
|||
One cannot obtain the limit by [[substitution|substituting]] 0 for ''h'', since it will result in [[division by zero]]. Instead, one must first modify the numerator to cancel ''h'' in the denominator. This process can be long and tedious for complicated functions, and many [[Derivative (examples)|short cuts]] are commonly used which simplify the process. |
|||
<math display="block">f(\mathbf{a} + \mathbf{v}) \approx f(\mathbf{a}) + f'(\mathbf{a})\mathbf{v}.</math> |
|||
Similarly with the single-variable derivative, <math> f'(\mathbf{a}) </math> is chosen so that the error in this approximation is as small as possible. The total derivative of <math> f </math> at <math> \mathbf{a} </math> is the unique linear transformation <math> f'(\mathbf{a}) \colon \R^n \to \R^m </math> such that{{sfn|Davvaz|2023|p=[https://books.google.com/books?id=ofzKEAAAQBAJ&pg=PA266 266]}} |
|||
<math display="block">\lim_{\mathbf{h}\to 0} \frac{\lVert f(\mathbf{a} + \mathbf{h}) - (f(\mathbf{a}) + f'(\mathbf{a})\mathbf{h})\rVert}{\lVert\mathbf{h}\rVert} = 0.</math> |
|||
Here <math> \mathbf{h} </math> is a vector in <math> \R^n </math>, so the norm in the denominator is the standard length on <math> \R^n </math>. However, <math> f'(\mathbf{a}) \mathbf{h} </math> is a vector in <math> \R^m </math>, and the norm in the numerator is the standard length on <math> \R^m </math>.{{sfn|Davvaz|2023|p=[https://books.google.com/books?id=ofzKEAAAQBAJ&pg=PA266 266]}} If <math> v </math> is a vector starting at <math> a </math>, then <math> f'(\mathbf{a}) \mathbf{v} </math> is called the [[pushforward (differential)|pushforward]] of <math> \mathbf{v} </math> by <math> f </math>.{{sfn|Lee|2013|p=72}} |
|||
If the total derivative exists at <math> \mathbf{a} </math>, then all the partial derivatives and directional derivatives of <math> f </math> exist at <math> \mathbf{a} </math>, and for all <math> \mathbf{v} </math>, <math> f'(\mathbf{a})\mathbf{v} </math> is the directional derivative of <math> f </math> in the direction <math> \mathbf{v} </math>. If <math> f </math> is written using coordinate functions, so that <math> f = (f_1, f_2, \dots, f_m) </math>, then the total derivative can be expressed using the partial derivatives as a [[matrix (mathematics)|matrix]]. This matrix is called the [[Jacobian matrix]] of <math> f </math> at <math> \mathbf{a} </math>:{{sfn|Davvaz|2023|p=[https://books.google.com/books?id=ofzKEAAAQBAJ&pg=PA267 267]}} |
|||
=== Examples === |
|||
<math display="block">f'(\mathbf{a}) = \operatorname{Jac}_{\mathbf{a}} = \left(\frac{\partial f_i}{\partial x_j}\right)_{ij}.</math> |
|||
<!-- The existence of the total derivative <math> f(\mathbf{a}) </math> is strictly stronger than the existence of all the partial derivatives, but if the partial derivatives exist and are continuous, then the total derivative exists, is given by the Jacobian, and depends continuously on <math> \mathbf{a} </math>. |
|||
The definition of the total derivative subsumes the definition of the derivative in one variable. That is, if <math> f </math> is a real-valued function of a real variable, then the total derivative exists if and only if the usual derivative exists. The Jacobian matrix reduces to a {{nowrap|1=1×1}} matrix whose only entry is the derivative <math> f'(x) </math>. This {{nowrap|1=1×1}} matrix satisfies the property that |
|||
Consider the graph of <math>f(x)=2x-3</math>. Using [[analytic geometry]], the slope of this line can be shown to be 2 at every point. The computations below get the same result using calculus, illustrating the use of the difference quotient. |
|||
<math display="block"> f(a+h) \approx f(a) + f'(a)h.</math> |
|||
Up to changing variables, this is the statement that the function <math>x \mapsto f(a) + f'(a)(x-a)</math> is the best linear approximation to <math> f </math> at <math> a </math>.{{cn|date=January 2024}} |
|||
The total derivative of a function does not give another function in the same way as the one-variable case. This is because the total derivative of a multivariable function has to record much more information than the derivative of a single-variable function. Instead, the total derivative gives a function from the [[tangent bundle]] of the source to the tangent bundle of the target.{{cn|date=January 2024}} |
|||
{| |
|||
|- |
|||
| <math>f'(x)\, </math> |
|||
| <math>= \lim_{h\to 0}\frac{f(x+h)-f(x)}{h} </math> |
|||
|- |
|||
| |
|||
| <math> = \lim_{h\to 0}\frac{2(x+h)-3-(2x-3)}{h} </math> |
|||
|- |
|||
| |
|||
| <math> = \lim_{h\to 0}\frac{2x+2h-3-(2x-3)}{h} </math> |
|||
|- |
|||
| |
|||
| <math> = \lim_{h\to 0}\frac{2h}{h} = 2. </math> |
|||
|} |
|||
The natural analog of second, third, and higher-order total derivatives is not a linear transformation, is not a function on the tangent bundle, and is not built by repeatedly taking the total derivative. The analog of a higher-order derivative, called a [[jet (mathematics)|jet]], cannot be a linear transformation because higher-order derivatives reflect subtle geometric information, such as concavity, which cannot be described in terms of linear data such as vectors. It cannot be a function on the tangent bundle because the tangent bundle only has room for the base space and the directional derivatives. Because jets capture higher-order information, they take as arguments additional coordinates representing higher-order changes in direction. The space determined by these additional coordinates is called the [[jet bundle]]. The relation between the total derivative and the partial derivatives of a function is paralleled in the relation between the {{nowrap|1=<math> k </math>-}}th order jet of a function and its partial derivatives of order less than or equal to <math> k </math>.{{cn|date=January 2024}} |
|||
The derivative and slope are equivalent. |
|||
By repeatedly taking the total derivative, one obtains higher versions of the [[Fréchet derivative]], specialized to <math> \R^p </math>. The {{nowrap|1=<math> k </math>-}}th order total derivative may be interpreted as a map |
|||
Now consider the function <math>f(x)=x^2</math>: |
|||
<math display="block"> D^k f: \mathbb{R}^n \to L^k(\mathbb{R}^n \times \cdots \times \mathbb{R}^n, \mathbb{R}^m), </math> |
|||
which takes a point <math> \mathbf{x} </math> in <math> \R^n </math> and assigns to it an element of the space of {{nowrap|1=<math> k </math>-}}linear maps from <math> \R^n </math> to <math> \R^m </math> — the "best" (in a certain precise sense) {{nowrap|1=<math> k </math>-}}linear approximation to <math> f </math> at that point. By precomposing it with the [[Diagonal functor|diagonal map]] <math> \Delta </math>, <math> \mathbf{x} \to (\mathbf{x}, \mathbf{x}) </math>, a generalized Taylor series may be begun as |
|||
<math display="block">\begin{align} |
|||
f(\mathbf{x}) & \approx f(\mathbf{a}) + (D f)(\mathbf{x-a}) + \left(D^2 f\right)(\Delta(\mathbf{x-a})) + \cdots\\ |
|||
& = f(\mathbf{a}) + (D f)(\mathbf{x - a}) + \left(D^2 f\right)(\mathbf{x - a}, \mathbf{x - a})+ \cdots\\ |
|||
& = f(\mathbf{a}) + \sum_i (D f)_i (x_i-a_i) + \sum_{j, k} \left(D^2 f\right)_{j k} (x_j-a_j) (x_k-a_k) + \cdots |
|||
\end{align}</math> |
|||
where <math> f(\mathbf{a}) </math> is identified with a constant function, <math> x_i - a_i </math> are the components of the vector <math> \mathbf{x}- \mathbf{a} </math>, and <math> (Df)_i </math> and <math> (D^2 f)_{jk} </math> are the components of <math> Df </math> and <math> D^2 f </math> as linear transformations.{{cn|date=January 2024}}--> |
|||
==Generalizations== |
|||
{| |
|||
{{Main|Generalizations of the derivative}} |
|||
|- |
|||
| <math> f'(x)\, </math> |
|||
| <math>= \lim_{h\to 0}\frac{f(x+h)-f(x)}{h} </math> |
|||
|- |
|||
| |
|||
| <math> = \lim_{h\to 0}\frac{(x+h)^2 - x^2}{h} </math> |
|||
|- |
|||
| |
|||
| <math> = \lim_{h\to 0}\frac{x^2 + 2xh + h^2 - x^2}{h} </math> |
|||
|- |
|||
| |
|||
| <math> = \lim_{h\to 0}\frac{2xh + h^2}{h} </math> |
|||
|- |
|||
| |
|||
| <math> = \lim_{h\to 0}(2x + h) = 2x. </math> |
|||
|} |
|||
The concept of a derivative can be extended to many other settings. The common thread is that the derivative of a function at a point serves as a [[linear approximation]] of the function at that point. |
|||
For any point ''x'', the slope of the function <math>f(x)=x^2</math> is <math>f'(x)=2x</math>. |
|||
* An important generalization of the derivative concerns [[complex function]]s of [[Complex number|complex variable]]s, such as functions from (a domain in) the complex numbers <math>\C</math> to <math>\C</math>. The notion of the derivative of such a function is obtained by replacing real variables with complex variables in the definition.{{sfn|Roussos|2014|p=303}} If <math>\C</math> is identified with <math>\R^2</math> by writing a complex number <math>z</math> as <math>x+iy</math>, then a differentiable function from <math>\C</math> to <math>\C</math> is certainly differentiable as a function from <math>\R^2</math> to <math>\R^2</math> (in the sense that its partial derivatives all exist), but the converse is not true in general: the complex derivative only exists if the real derivative is ''complex linear'' and this imposes relations between the partial derivatives called the [[Cauchy–Riemann equations]] – see [[holomorphic function]]s.{{sfn|Gbur|2011|pp=261–264}} |
|||
* Another generalization concerns functions between [[smooth manifold|differentiable or smooth manifolds]]. Intuitively speaking such a manifold <math>M</math> is a space that can be approximated near each point <math>x</math> by a vector space called its [[tangent space]]: the prototypical example is a [[smooth surface]] in <math>\R^3</math>. The derivative (or differential) of a (differentiable) map <math>f:M\to N</math> between manifolds, at a point <math>x</math> in <math>M</math>, is then a [[linear map]] from the tangent space of <math>M</math> at <math>x</math> to the tangent space of <math>N</math> at <math>f(x)</math>. The derivative function becomes a map between the [[tangent bundle]]s of <math>M</math> and <math>N</math>. This definition is used in [[differential geometry]].{{sfn|Gray|Abbena|Salamon|2006|p=[https://books.google.com/books?id=owEj9TMYo7IC&pg=PA826 826]}} |
|||
* Differentiation can also be defined for maps between [[vector space]], such as [[Banach space]], in which those generalizations are the [[Gateaux derivative]] and the [[Fréchet derivative]].<ref>{{harvnb|Azegami|2020}}. See p. [https://books.google.com/books?id=e08AEAAAQBAJ&pg=PA209 209] for the Gateaux derivative, and p. [https://books.google.com/books?id=e08AEAAAQBAJ&pg=PA211 211] for the Fréchet derivative.</ref> |
|||
* One deficiency of the classical derivative is that very many functions are not differentiable. Nevertheless, there is a way of extending the notion of the derivative so that all [[continuous function|continuous]] functions and many other functions can be differentiated using a concept known as the [[weak derivative]]. The idea is to embed the continuous functions in a larger space called the space of [[distribution (mathematics)|distributions]] and only require that a function is differentiable "on average".{{sfn|Funaro|1992|p=[https://books.google.com/books?id=CX4SXf3mdeUC&pg=PA84 84–85]}} |
|||
* Properties of the derivative have inspired the introduction and study of many similar objects in algebra and topology; an example is [[differential algebra]]. Here, it consists of the derivation of some topics in abstract algebra, such as [[Ring (mathematics)|rings]], [[Ideal (ring theory)|ideals]], [[Field (mathematics)|field]], and so on.{{sfn|Kolchin|1973|p=[https://books.google.com/books?id=yDCfhIjka-8C&pg=PA58 58], [https://books.google.com/books?id=yDCfhIjka-8C&pg=PA126 126]}} |
|||
* The discrete equivalent of differentiation is [[finite difference]]s. The study of differential calculus is unified with the calculus of finite differences in [[time scale calculus]].{{sfn|Georgiev|2018|p=[https://books.google.com/books?id=OJJVDwAAQBAJ&pg=PA8 8]}} |
|||
* The [[arithmetic derivative]] involves the function that is defined for the [[Integer|integers]] by the [[prime factorization]]. This is an analogy with the product rule.{{sfn|Barbeau|1961}} |
|||
==See also== |
|||
== Notations for differentiation == |
|||
* [[Integral]] |
|||
=== Lagrange's notation === |
|||
== Notes == |
|||
The simplest notation for differentiation that is in current use is due to [[Joseph Louis Lagrange]] and uses the [[Prime (symbol)|prime mark]]: |
|||
{{reflist}} |
|||
{| |
|||
|- |
|||
| style="text-align: right; height: 2.75em"|<math>f'(x) \;</math> |
|||
| for the first derivative, |
|||
|- |
|||
| style="text-align: right; height: 2.75em"|<math>f''(x) \;</math> |
|||
| for the second derivative, |
|||
|- |
|||
| style="text-align: right; height: 2.75em"|<math>f'''(x) \;</math> |
|||
| for the third derivative, and in general |
|||
|- |
|||
| style="text-align: right; height: 2.75em"|<math>f^{(n)}(x) \;</math> |
|||
| for the ''n''th derivative. |
|||
|} |
|||
=== Leibniz's notation === |
|||
The other common notation is [[Leibniz's notation for differentiation]] which is named after [[Gottfried Leibniz]]. For the function whose value at ''x'' is the derivative of ''f'' at ''x'', we write: |
|||
: <math>\frac{d\left(f(x)\right)}{dx}.</math> |
|||
With Leibniz's notation, we can write the derivative of ''f'' at the point ''a'' in two different ways: |
|||
: <math>\frac{d\left(f(x)\right)}{dx}\left.{\!\!\frac{}{}}\right|_{x=a} = \left(\frac{d\left(f(x)\right)}{dx}\right)(a).</math> |
|||
If the output of ''f''(''x'') is another variable, for example, if ''y''=''f''(''x''), we can write the derivative as: |
|||
: <math>\frac{dy}{dx}.</math> |
|||
Higher derivatives are expressed as |
|||
: <math>\frac{d^n\left(f(x)\right)}{dx^n}</math> or <math>\frac{d^ny}{dx^n}</math> |
|||
for the ''n''-th derivative of ''f''(''x'') or ''y'' respectively. Historically, this came from the fact that, for example, the 3rd derivative is: |
|||
: <math>\frac{d \left(\frac{d \left( \frac{d \left(f(x)\right)} {dx}\right)} {dx}\right)} {dx}</math> |
|||
which we can loosely write as: |
|||
: <math>\left(\frac{d}{dx}\right)^3 \left(f(x)\right) = |
|||
\frac{d^3}{\left(dx\right)^3} \left(f(x)\right).</math> |
|||
Dropping brackets gives the notation above. |
|||
Leibniz's notation allows one to specify the variable for differentiation (in the denominator). This is especially relevant for [[partial derivative|partial differentiation]]. It also makes the [[chain rule]] easy to remember: |
|||
: <math>\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}.</math> |
|||
(In the formulation of calculus in terms of limits, the ''du'' symbol has been assigned various meanings by various authors. Some authors do not assign a meaning to ''du'' by itself, but only as part of the symbol ''du/dx''. Others define "dx" as an independent variable, and define ''du'' by ''du'' = ''dx''•''f'' '(''x''). In [[non-standard analysis]] ''du'' is defined as an infinitesimal.) |
|||
=== Newton's notation === |
|||
[[Newton's notation for differentiation]] (also called the dot notation for differentiation) requires placing a dot over the function name: |
|||
: <math>\dot{x} = \frac{dx}{dt} = x'(t)</math> |
|||
: <math>\ddot{x} = \frac{d^2x}{dt^2} = x''(t)</math> |
|||
and so on. |
|||
Newton's notation is mainly used in [[mechanics]], normally for time derivatives such as velocity and acceleration, and in [[ODE]] theory. It is usually only used for first and second derivatives, and then, only to denote derivatives with respect to time. |
|||
=== Euler's notation === |
|||
[[Leonhard Euler|Euler]]'s notation uses a [[differential operator]], denoted as ''D'', which is prefixed to the function with the variable as a subscript of the operator: |
|||
{| |
|||
|- |
|||
| style="text-align: right; height: 2.75em"|<math>D_x f(x) \;</math> |
|||
| for the first derivative, |
|||
|- |
|||
| style="text-align: right; height: 2.75em"|<math>D_x^2 f(x) \;</math> |
|||
| for the second derivative, and |
|||
|- |
|||
| style="text-align: right; height: 2.75em"|<math>D_x^n f(x) \;</math> |
|||
| for the ''n''th derivative, provided ''n'' ≥ 2. |
|||
|} |
|||
This notation can also be abbreviated when taking derivatives of expressions that contain a single variable. The subscript to the operator is dropped and is assumed to be the only variable present in the expression. In the following examples, ''u'' represents any expression of a single variable: |
|||
{| |
|||
|- |
|||
| style="text-align: right; height: 2.75em"|<math>D u \;</math> |
|||
| for the first derivative, |
|||
|- |
|||
| style="text-align: right; height: 2.75em"|<math>D^2 u \;</math> |
|||
| for the second derivative, and |
|||
|- |
|||
| style="text-align: right; height: 2.75em"|<math>D^n u \;</math> |
|||
| for the ''n''th derivative, provided ''n'' ≥ 2. |
|||
|} |
|||
Euler's notation is useful for stating and solving [[linear differential equation]]s. |
|||
== Critical points == |
|||
Points on the [[graph of a function|graph]] of a function where the derivative is equal to [[0 (number)|zero]] or the derivative does not exist are called ''[[critical point (mathematics)|critical points]]'' or sometimes ''[[stationary point]]s''. If the second derivative is positive at a critical point, that point is a [[local minimum]]; if negative, it is a [[local maximum]]; if zero, it may or may not be a local minimum or local maximum. Taking derivatives and solving for critical points is often a simple way to find local minima or maxima, which can be useful in [[Optimization (mathematics)|optimization]]. In fact, local minima and maxima can only occur at critical points or endpoints. This is related to the [[extreme value theorem]]. |
|||
== Physics == |
|||
Arguably the most important application of calculus to [[physics]] is the concept of the "'''time derivative'''"—the rate of change over time—which is required for the precise definition of several important concepts. In particular, the time derivatives of an object's position are significant in [[Newtonian physics]]: |
|||
* [[Velocity]] is the derivative (with respect to time) of an object's displacement (distance from the original position). |
|||
* [[Acceleration]] is the derivative (with respect to time) of an object's velocity, that is, the second derivative (with respect to time) of an object's position. |
|||
* [[Jerk]] is the derivative (with respect to time) of an object's acceleration, that is, the third derivative (with respect to time) of an object's position, and second derivative (with respect to time) of an object's velocity. |
|||
For example, if an object's position on a curve is given by |
|||
: <math>x(t) = -16t^2 + 16t + 32 , \,\!</math> |
|||
then the object's velocity is |
|||
: <math>\dot x(t) = x'(t) = -32t + 16, \,\!</math> |
|||
and the object's acceleration is |
|||
: <math>\ddot x(t) = x''(t) = -32 . \,\!</math> |
|||
Since the acceleration is constant, the jerk of the object is zero. |
|||
== Rules for finding the derivative == |
|||
In many cases, complicated limit calculations by direct application of Newton's difference quotient can be avoided using differentiation rules. |
|||
* ''Constant rule'': |
|||
:<math>c' = 0 \,</math> for any real number ''c'' |
|||
* ''Constant multiple rule'': |
|||
:<math>(cf)' = c(f') \,</math> for any [[real number]] ''c'' (a consequence of the linearity rule below). |
|||
* ''[[Linearity of differentiation|Linearity]]'': |
|||
:<math>(af + bg)' = af' + bg' \,</math> for all functions ''f'' and ''g'' and all real numbers ''a'' and ''b''. |
|||
* ''[[Calculus with polynomials|Power rule]]'': If <math>f(x) = x^n</math>, for any [[integer number]] ''n''; |
|||
:<math>f'(x) = nx^{n-1} \,</math>. |
|||
* ''[[Product rule]]'': |
|||
:<math> (fg)' = f 'g + fg' \,</math> for all functions ''f'' and ''g''. |
|||
* ''[[Quotient rule]]'': |
|||
:<math>\left( \frac{f} {g} \right)' = \frac{ (f 'g - fg') } {(g^2) } \,</math> unless ''g'' is zero. |
|||
* ''[[Chain rule]]'': If <math>f(x) = h(g(x))</math>, then |
|||
:<math>f'(x) = h'(g(x)) g'(x) \,</math>. |
|||
* ''[[Inverse function]]'': If the function <math>f(x)</math> has an inverse <math>g(x) = f^{-1}(x)</math>, then |
|||
:<math>g'(x) = \frac{1}{f'(f^{-1}(x))} </math>. |
|||
In addition, the derivatives of some common functions are useful to know. See the [[table of derivatives]]. |
|||
As an example, the derivative of |
|||
: <math>f(x) = x^4 + \sin (x^2) - \ln(x) e^x + 7\,</math> |
|||
is |
|||
: <math> |
|||
\begin{align} |
|||
f'(x) &= 4 x^{(4-1)}+ \frac{d\left(x^2\right)}{dx}\cos{x^2} - \frac{d\left(\ln {x}\right)}{dx} e^x - \ln{x} \frac{d\left(e^x\right)}{dx} + 0 \\ |
|||
&= 4x^3 + 2x\cos {x^2} - \frac{1}{x} e^x - \ln(x) e^x. |
|||
\end{align} |
|||
</math> |
|||
The first term was calculated using the power rule, the second using the chain rule and the last two come from the product rule. The derivatives of sin(''x''), ln(''x'') and exp(''x'') can be found in [[table of derivatives]]. |
|||
== Using derivatives to graph functions == |
|||
Derivatives are a useful tool for examining the [[graph of a function|graphs of functions]]. In particular, the points in the interior of the domain of a real-valued function which take that function to local [[extremum|extrema]] will all have a first derivative of zero. However, not all critical points are local extrema; for example, ''f(x)=x<sup>3</sup>'' has a critical point at ''x=0'', but it has neither a maximum nor a minimum there. The [[first derivative test]] and the [[second derivative test]] provide ways to determine if the critical points are maxima, minima or neither. |
|||
In the case of multidimensional domains, the function will have a partial derivative of zero with respect to each dimension at local extrema. In this case, the Second Derivative Test can still be used to characterize critical points, by considering the [[eigenvalue]]s of the [[Hessian matrix]] of second partial derivatives of the function at the critical point. If all of the eigenvalues are positive, then the point is a local minimum; if all are negative, it is a local maximum. If there are some positive and some negative eigenvalues, then the critical point is a [[saddle point]], and if none of these cases hold then the test is inconclusive (e.g., eigenvalues of 0 and 3). |
|||
Once the local extrema have been found, it is usually rather easy to get a rough idea of the general graph of the function, since (in the single-dimensional domain case) it will be uniformly increasing or decreasing except at critical points, and hence (assuming it is [[continuity (mathematics)|continuous]]) will have values in between its values at the critical points on either side. |
|||
== Generalizations == |
|||
{{see details|derivative (generalizations)}} |
|||
Where a function depends on more than one variable, the concept of a '''[[partial derivative]]''' is used. Partial derivatives can be thought of informally as taking the derivative of the function with all but one variable held temporarily constant near a point. Partial derivatives are represented as ∂/∂x (where ∂ is a rounded 'd' known as the 'partial derivative symbol'). Some people pronounce the partial derivative symbol as 'del' rather than the 'dee' used for the standard derivative symbol, 'd'. |
|||
The concept of derivative can be extended to more general settings. The common thread is that the derivative at a point serves as a [[linear approximation]] of the function at that point. Perhaps the most natural situation is that of functions between differentiable [[manifold]]s; the derivative at a certain point then becomes a [[linear transformation]] between the corresponding [[tangent space]]s and the derivative function becomes a map between the [[tangent bundle]]s. |
|||
In order to differentiate all [[continuous function|continuous]] functions and much more, one defines the concept of [[distribution (mathematics)|distribution]] and [[weak derivative]]s. |
|||
For [[complex number|complex]] functions of a complex variable differentiability is a much stronger condition than that the real and [[imaginary part]] of the function are differentiable with respect to the real and imaginary part of the argument. For example, the function ''f''(''x'' + ''iy'') = ''x'' + 2''iy'' satisfies the latter, but not the first. See also the article on [[holomorphic function]]s. |
|||
== See also == |
|||
* [[Derivative (examples)]] |
|||
* [[Derivative (generalizations)]] |
|||
* [[Partial derivative]] |
|||
* [[Total derivative]] |
|||
* [[Table of derivatives]] |
|||
* [[Smooth function]] |
|||
* [[Differential calculus]] |
|||
* [[Differintegral]] |
|||
* [[Automatic differentiation]] |
|||
* [[Reciprocal rule]] |
|||
* [[Chain rule]] |
|||
* [[History of calculus]] |
|||
== References == |
== References == |
||
{{refbegin|30em}} |
|||
<references/> |
|||
*{{Citation |
|||
=== Print === |
|||
| last = Apostol |
|||
| first = Tom M. |
|||
| author-link = Tom M. Apostol |
|||
| date = June 1967 |
|||
| title = Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra |
|||
| publisher = Wiley |
|||
| edition = 2nd |
|||
| volume = 1 |
|||
| isbn = 978-0-471-00005-1 |
|||
| url-access = registration |
|||
| url = https://archive.org/details/calculus01apos |
|||
}} |
|||
* {{citation |
|||
| last = Azegami | first = Hideyuki |
|||
| year = 2020 |
|||
| title = Shape Optimization Problems |
|||
| series = Springer Optimization and Its Applications |
|||
| volume = 164 |
|||
| publisher = Springer |
|||
| url = https://books.google.com/books?id=e08AEAAAQBAJ |
|||
| doi = 10.1007/978-981-15-7618-8 |
|||
| isbn = 978-981-15-7618-8 |
|||
| s2cid = 226442409 |
|||
}} |
|||
*{{Citation |
|||
| last = Banach |first = Stefan | author-link = Stefan Banach |
|||
| title = Uber die Baire'sche Kategorie gewisser Funktionenmengen |
|||
| journal = Studia Math. |
|||
| volume = 3 |
|||
| issue = 3 |
|||
| year = 1931 |
|||
| pages = 174–179 |
|||
| doi = 10.4064/sm-3-1-174-179 |
|||
| postscript = . |
|||
| url = https://scholar.google.com/scholar?output=instlink&q=info:SkKdCEmUd6QJ:scholar.google.com/&hl=en&as_sdt=0,50&scillfp=3432975470163241186&oi=lle |
|||
| doi-access = free}} |
|||
* {{cite journal |
|||
| last = Barbeau | first = E. J. |
|||
| title = Remarks on an arithmetic derivative |
|||
| journal = [[Canadian Mathematical Bulletin]] |
|||
| volume = 4 |
|||
| year = 1961 |
|||
| issue = 2 |
|||
| pages = 117–122 |
|||
| doi = 10.4153/CMB-1961-013-0 |
|||
| zbl = 0101.03702 |
|||
| doi-access = free |
|||
}} |
|||
* {{citation |
|||
| last = Bhardwaj | first = R. S. |
|||
| year = 2005 |
|||
| title = Mathematics for Economics & Business |
|||
| edition = 2nd |
|||
| publisher = Excel Books India |
|||
| isbn = 9788174464507 |
|||
}} |
|||
*{{Citation |
|||
| last = Cajori | first = Florian |
|||
| author-link = Florian Cajori |
|||
| year = 1923 |
|||
| title = The History of Notations of the Calculus |
|||
| journal = Annals of Mathematics |
|||
| volume = 25 |
|||
| issue = 1 |
|||
| pages = 1–46 |
|||
| doi = 10.2307/1967725 |
|||
| jstor = 1967725 |
|||
| hdl = 2027/mdp.39015017345896 |
|||
| hdl-access = free |
|||
}} |
|||
*{{Citation |
|||
| last = Cajori |
|||
| first = Florian |
|||
| title = A History of Mathematical Notations |
|||
| year = 2007 |
|||
| url = https://books.google.com/books?id=RUz1Us2UDh4C&pg=PA204 |
|||
| volume = 2 |
|||
| publisher = Cosimo Classics |
|||
| isbn = 978-1-60206-713-4}} |
|||
* {{citation |
|||
| last = Carothers | first = N. L. |
|||
| year = 2000 |
|||
| title = Real Analysis |
|||
| publisher = Cambridge University Press |
|||
}} |
|||
*{{Citation |
|||
| last1 = Choudary | first1 = A. D. R. |
|||
| last2 = Niculescu | first2 = Constantin P. |
|||
| year = 2014 |
|||
| title = Real Analysis on Intervals |
|||
| publisher = Springer India |
|||
| doi = 10.1007/978-81-322-2148-7 |
|||
| isbn = 978-81-322-2148-7 |
|||
}} |
|||
* {{citation |
|||
| last = Christopher | first = Essex |
|||
| year = 2013 |
|||
| title = Calculus: A complete course |
|||
| page = 682 |
|||
| publisher = Pearson |
|||
| isbn = 9780321781079 |
|||
| oclc = 872345701 |
|||
}} |
|||
*{{Citation |
|||
| last1 = Courant |
|||
| first1 = Richard |
|||
| author-link1 = Richard Courant |
|||
| last2 = John |
|||
| first2 = Fritz |
|||
| author-link2 = Fritz John |
|||
| date = December 22, 1998 |
|||
| title = Introduction to Calculus and Analysis, Vol. 1 |
|||
| publisher = [[Springer-Verlag]] |
|||
| isbn = 978-3-540-65058-4 |
|||
| doi = 10.1007/978-1-4613-8955-2 |
|||
}} |
|||
* {{citation |
|||
| last = David | first = Claire |
|||
| year = 2018 |
|||
| title = Bypassing dynamical systems: A simple way to get the box-counting dimension of the graph of the Weierstrass function |
|||
| journal = Proceedings of the International Geometry Center |
|||
| publisher = Academy of Sciences of Ukraine |
|||
| volume = 11 |
|||
| issue = 2 |
|||
| pages = 53–68 |
|||
| doi = 10.15673/tmgc.v11i2.1028 |
|||
| doi-access = free |
|||
| arxiv = 1711.10349 |
|||
}} |
|||
* {{citation |
|||
| last = Davvaz | first = Bijan |
|||
| year = 2023 |
|||
| title = Vectors and Functions of Several Variables |
|||
| publisher = Springer |
|||
| doi = 10.1007/978-981-99-2935-1 |
|||
| isbn = 978-981-99-2935-1 |
|||
| s2cid = 259885793 |
|||
}} |
|||
* {{citation |
|||
| last1 = Debnath | first1 = Lokenath |
|||
| last2 = Shah | first2 = Firdous Ahmad |
|||
| year = 2015 |
|||
| title = Wavelet Transforms and Their Applications |
|||
| edition = 2nd |
|||
| publisher = Birkhäuser |
|||
| url = https://books.google.com/books?id=qPuWBQAAQBAJ |
|||
| doi = 10.1007/978-0-8176-8418-1 |
|||
| isbn = 978-0-8176-8418-1 |
|||
}} |
|||
* {{Citation |
|||
| last = Evans |
|||
| first = Lawrence |
|||
| author-link = Lawrence Evans |
|||
| title = Partial Differential Equations |
|||
| publisher = American Mathematical Society |
|||
| year = 1999 |
|||
| isbn = 0-8218-0772-2 |
|||
}} |
|||
*{{Citation |
|||
| last = Eves |
|||
| first = Howard |
|||
| date = January 2, 1990 |
|||
| title = An Introduction to the History of Mathematics |
|||
| edition = 6th |
|||
| publisher = Brooks Cole |
|||
| isbn = 978-0-03-029558-4 |
|||
}} |
|||
* {{citation |
|||
| last = Funaro | first = Daniele |
|||
| year = 1992 |
|||
| title = Polynomial Approximation of Differential Equations |
|||
| series = Lecture Notes in Physics Monographs |
|||
| volume = 8 |
|||
| publisher = Springer |
|||
| url = https://books.google.com/books?id=CX4SXf3mdeUC |
|||
| doi = 10.1007/978-3-540-46783-0 |
|||
| isbn = 978-3-540-46783-0 |
|||
}} |
|||
*{{citation |
|||
| last = Gbur |
|||
| first = Greg |
|||
| author-link = Greg Gbur |
|||
| year = 2011 |
|||
| title = Mathematical Methods for Optical Physics and Engineering |
|||
| publisher = Cambridge University Press |
|||
| bibcode = 2011mmop.book.....G |
|||
| isbn = 978-1-139-49269-0 |
|||
}} |
|||
* {{citation |
|||
| last = Georgiev | first = Svetlin G. |
|||
| year = 2018 |
|||
| title = Fractional Dynamic Calculus and Fractional Dynamic Equations on Time Scales |
|||
| url = https://books.google.com/books?id=OJJVDwAAQBAJ |
|||
| publisher = Springer |
|||
| doi = 10.1007/978-3-319-73954-0 |
|||
| isbn = 978-3-319-73954-0 |
|||
}} |
|||
* {{citation |
|||
| last = Goodman | first = A. W. |
|||
| year = 1963 |
|||
| title = Analytic Geometry and the Calculus |
|||
| publisher = The MacMillan Company |
|||
| url = https://books.google.com/books?id=v7i2YJJg_gcC |
|||
}} |
|||
*{{citation |
|||
| last = Gonick |
|||
| first = Larry |
|||
| author-link = Larry Gonick |
|||
| year = 2012 |
|||
| title = The Cartoon Guide to Calculus |
|||
| publisher = William Morrow |
|||
| url = https://www.larrygonick.com/titles/science/cartoon-guide-to-calculus-2/ |
|||
| isbn = 978-0-06-168909-3 |
|||
}} |
|||
* {{citation |
|||
| last1 = Gray | first1 = Alfred |
|||
| last2 = Abbena | first2 = Elsa |
|||
| last3 = Salamon | first3 = Simon |
|||
| year = 2006 |
|||
| title = Modern Differential Geometry of Curves and Surfaces with Mathematica |
|||
| publisher = CRC Press |
|||
| isbn = 978-1-58488-448-4 |
|||
| url = https://books.google.com/books?id=owEj9TMYo7IC |
|||
}} |
|||
* {{citation |
|||
| last = Guzman | first = Alberto |
|||
| year = 2003 |
|||
| title = Derivatives and Integrals of Multivariable Functions |
|||
| url = https://books.google.com/books?id=aI_qBwAAQBAJ |
|||
| publisher = Springer |
|||
| doi = 10.1007/978-1-4612-0035-2 |
|||
| isbn = 978-1-4612-0035-2 |
|||
}} |
|||
* {{citation |
|||
| last1 = Henle | first1 = James M. |
|||
| last2 = Kleinberg | first2 = Eugene M. |
|||
| year = 2003 |
|||
| title = Infinitesimal Calculus |
|||
| publisher = Dover Publications |
|||
| isbn = 978-0-486-42886-4 |
|||
}} |
|||
*{{Citation |
|||
| last1 = Hewitt | first1 = Edwin | author-link1 = Edwin Hewitt |
|||
| last2 = Stromberg | first2 = Karl R. |
|||
| title = Real and abstract analysis |
|||
| publisher = Springer-Verlag |
|||
| year = 1965 |
|||
| pages = Theorem 17.8 |
|||
| doi = 10.1007/978-3-662-29794-0 |
|||
| isbn = 978-3-662-28275-5 | no-pp = true}} |
|||
* {{citation |
|||
| last = Jašek | first = Martin |
|||
| year = 1922 |
|||
| url = http://dml.cz/bitstream/handle/10338.dmlcz/121916/CasPestMatFys_051-1922-2_2.pdf |
|||
| title = Funkce Bolzanova |
|||
| journal = Časopis pro Pěstování Matematiky a Fyziky |
|||
| volume = 51 |
|||
| issue = 2 |
|||
| pages = 69–76 |
|||
| doi = 10.21136/CPMF.1922.121916 |
|||
| lang = cs |
|||
}} |
|||
* {{citation |
|||
| last = Jarník | first = Vojtěch | authorlink = Vojtěch Jarník |
|||
| year = 1922 |
|||
| title = O funkci Bolzanově |
|||
| journal = Časopis pro Pěstování Matematiky a Fyziky |
|||
| volume = 51 |
|||
| issue = 4 |
|||
| pages = 248–264 |
|||
| doi = 10.21136/CPMF.1922.109021 | lang = cs |
|||
| url = http://dml.cz/bitstream/handle/10338.dmlcz/109021/CasPestMatFys_051-1922-4_5.pdf}}. See the English version [http://dml.cz/bitstream/handle/10338.dmlcz/400073/Bolzano_15-1981-1_6.pdf here]. |
|||
*{{Citation |
|||
| last = Keisler |
|||
| first = H. Jerome |
|||
| year = 2012 |
|||
| orig-year = 1986 |
|||
| publisher = Prindle, Weber & Schmidt |
|||
| edition = 2nd |
|||
| title = Elementary Calculus: An Approach Using Infinitesimals |
|||
| isbn = 978-0-871-50911-6 |
|||
| url = http://www.math.wisc.edu/~keisler/calc.html |
|||
}} |
|||
* {{citation |
|||
| last = Kolchin | first = Ellis |
|||
| title = Differential Algebra And Algebraic Groups |
|||
| year = 1973 |
|||
| url = https://books.google.com/books?id=yDCfhIjka-8C |
|||
| publisher = Academic Press |
|||
| isbn = 978-0-08-087369-5 |
|||
}} |
|||
* {{Citation |
|||
| last = Kreyszig |
|||
| first = Erwin |
|||
| title = Differential Geometry |
|||
| publisher = [[Dover Publications|Dover]] |
|||
| year = 1991 |
|||
| isbn = 0-486-66721-9 |
|||
| location = New York |
|||
}} |
|||
*{{Citation |
|||
| last1 = Larson |
|||
| first1 = Ron |
|||
| last2 = Hostetler |
|||
| first2 = Robert P. |
|||
| last3 = Edwards |
|||
| first3 = Bruce H. |
|||
| date = February 28, 2006 |
|||
| title = Calculus: Early Transcendental Functions |
|||
| edition = 4th |
|||
| publisher = Houghton Mifflin Company |
|||
| isbn = 978-0-618-60624-5 |
|||
}} |
|||
* {{citation |
|||
| last = Lee |
|||
| first = John M. |
|||
| title = Introduction to Smooth Manifolds |
|||
| series = Graduate Texts in Mathematics |
|||
| year = 2013 |
|||
| volume = 218 |
|||
| publisher = Springer |
|||
| doi = 10.1007/978-0-387-21752-9 |
|||
| isbn = 978-0-387-21752-9 |
|||
}} |
|||
* {{citation |
|||
| last1 = Mathai | first1 = A. M. |
|||
| last2 = Haubold | first2 = H. J. |
|||
| year = 2017 |
|||
| title = Fractional and Multivariable Calculus: Model Building and Optimization Problems |
|||
| url = https://books.google.com/books?id=v20uDwAAQBAJ |
|||
| publisher = Springer |
|||
| doi = 10.1007/978-3-319-59993-9 |
|||
| isbn = 978-3-319-59993-9 |
|||
}} |
|||
* {{citation |
|||
| last1 = Moore | first1 = Will H. |
|||
| last2 = Siegel | first2 = David A. |
|||
| year = 2013 |
|||
| title = A Mathematical Course for Political and Social Research |
|||
| publisher = Princeton University Press |
|||
| url = https://books.google.com/books?id=emmYDwAAQBAJ |
|||
| isbn = 978-0-691-15995-9 |
|||
}} |
|||
*{{Citation |
|||
| last = Roussos |
|||
| first = Ioannis M. |
|||
| title = Improper Riemann Integral |
|||
| year = 2014 |
|||
| publisher = [[CRC Press]] |
|||
| url = https://books.google.com/books?id=nX1cAgAAQBAJ |
|||
| isbn = 978-1-4665-8807-3 |
|||
}} |
|||
* {{citation |
|||
| last = Rychlík | first = Karel |
|||
| year = 1923 |
|||
| title = Über eine Funktion aus Bolzanos handschriftlichem Nachlasse |
|||
}} |
|||
* {{citation |
|||
| last = Schwartzman | first = Steven |
|||
| year = 1994 |
|||
| title = The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English |
|||
| publisher = Mathematical Association of American |
|||
| isbn = 9781614445012 |
|||
| url = https://books.google.com/books?id=PsH2DwAAQBAJ |
|||
}} |
|||
* {{citation |
|||
| last = Silverman | first = Richard A. |
|||
| year = 1989 |
|||
| title = Essential Calculus: With Applications |
|||
| publisher = Courier Corporation |
|||
| isbn = 9780486660974 |
|||
}} |
|||
*{{Citation |
|||
| last = Stewart |
|||
| first = James |
|||
| author-link = James Stewart (mathematician) |
|||
| date = December 24, 2002 |
|||
| title = Calculus |
|||
| publisher = Brooks Cole |
|||
| edition = 5th |
|||
| isbn = 978-0-534-39339-7 |
|||
| url-access = registration |
|||
| url = https://archive.org/details/calculus0000stew |
|||
}} |
|||
*{{Citation |
|||
| last1 = Strang |
|||
| first1 = Gilbert |
|||
| author-link1 = Gilbert Strang |
|||
| display-authors = etal |
|||
| title = Calculus, volume 1 |
|||
| publisher = OpenStax |
|||
| year = 2023 |
|||
| isbn = 978-1-947172-13-5 |
|||
| url = https://openstax.org/details/books/calculus-volume-1 |
|||
| ref = {{sfnref|Strang et al.|2023}} |
|||
}} |
|||
*{{Citation |
|||
| last = Thompson |
|||
| first = Silvanus P. |
|||
| author-link = Silvanus P. Thompson |
|||
| date = September 8, 1998 |
|||
| title = [[Calculus Made Easy]] |
|||
| edition = Revised, Updated, Expanded |
|||
| place = New York |
|||
| publisher = St. Martin's Press |
|||
| isbn = 978-0-312-18548-0 |
|||
}} |
|||
* {{Citation |
|||
| last1 = Varberg |
|||
| first1 = Dale E. |
|||
| last2 = Purcell |
|||
| first2 = Edwin J. |
|||
| last3 = Rigdon |
|||
| first3 = Steven E. |
|||
| title = Calculus |
|||
| year = 2007 |
|||
| publisher = [[Pearson Prentice Hall]] |
|||
| edition = 9th |
|||
| isbn = 978-0131469686 |
|||
}} |
|||
* {{Citation |
|||
| last = Warner |
|||
| first = Frank W. |
|||
| author-link = Frank Wilson Warner |
|||
| year = 1983 |
|||
| title = Foundations of Differentiable Manifolds and Lie Groups |
|||
| publisher = Springer |
|||
| isbn = 978-0-387-90894-6 |
|||
| url = https://books.google.com/books?id=t6PNrjnfhuIC |
|||
}} |
|||
{{Refend}} |
|||
==External links== |
|||
* [[Michael Spivak|Spivak, Michael]], ''Calculus'' (3rd edition, 1994) Publish or Perish Press. ISBN 0-914098-89-6. |
|||
{{Sister project links|Differentiation|auto=1|wikt=y|b=y|v=y}} |
|||
*{{springer|title=Derivative|id=p/d031260}} |
|||
*[[Khan Academy]]: [https://www.khanacademy.org/math/differential-calculus/taking-derivatives/intro_differential_calc/v/newton-leibniz-and-usain-bolt "Newton, Leibniz, and Usain Bolt"] |
|||
*{{MathWorld |title=Derivative |id=Derivative}} |
|||
*[http://www.wolframalpha.com/calculators/derivative-calculator/ Online Derivative Calculator] from [[Wolfram Alpha]]. |
|||
{{good article}} |
|||
* Thompson, Silvanus Phillips, ''Calculus made easy : being a very-simplest introduction to those beautiful methods of reckoning which are generally called by the terrifying names of the differential calculus and the integral calculus'' New York : St. Martin's Press, 1998 ISBN 0-312-18548-0. Introduced by [[Martin Gardner]]. |
|||
{{Calculus topics}} |
|||
* Larson, Ron; Hostetler, Robert P.; and Edwards, Bruce H. (2003). ''Calculus of a Single Variable: Early Transcendental Functions'' (3rd edition). Houghton Mifflin Company. ISBN 0-618-22307-X. |
|||
{{Analysis-footer}} |
|||
{{Authority control}} |
|||
[[Category:Mathematical analysis]] |
|||
* Anton, Howard (1980). ''Calculus with analytical [[geometry]].''. New York:John Wiley and Sons. ISBN 0-471-03248-4. |
|||
[[Category:Differential calculus]] |
|||
=== Online books === |
|||
* Keisler, H. Jerome, [http://www.math.wisc.edu/~keisler/calc.html Elementary Calculus: An Approach Using Infinitesimals], University of Wisconsin |
|||
* Stroyan, K.D., [http://www.math.uiowa.edu/~stroyan/InfsmlCalculus/InfsmlCalc.htm A Brief Introduction to Infinitesimal Calculus], University of Iowa |
|||
* Mauch, Sean, [http://www.its.caltech.edu/~sean/book/unabridged.html ''Sean's Applied Math Book''], CIT, an online textbook that includes a complete introduction to calculus |
|||
* Crowell, Benjamin, [http://www.lightandmatter.com/calc/ ''Calculus''], Fullerton College, an online textbook |
|||
* Garrett, Paul, [http://www.math.umn.edu/~garrett/calculus/ Notes on First-Year Calculus] |
|||
* Hussain, Faraz, [http://www.understandingcalculus.com Understanding Calculus], an online textbook |
|||
* Sloughter, Dan, [http://math.furman.edu/~dcs/book Difference Equations to Differential Equations], an introduction to calculus |
|||
* [http://en.wikibooks.org/wiki/Calculus Wikibook of Calculus] |
|||
== External links == |
|||
* [http://www.calc101.com/webMathematica/derivatives.jsp Solving derivatives step-by-step]. |
|||
* [http://wims.unice.fr/wims/wims.cgi?module=tool/analysis/function.en WIMS Function Calculator] makes online calculation of derivatives; this software also enables interactive exercises. |
|||
* [http://www.adiff.com ADIFF] online symbolic derivatives calculator. |
|||
* [http://homepage.mac.com/stray/ib/maths/deriv_fp.pdf Proving Derivatives from First Principles]. |
|||
[[Category:Differential calculus | *]] |
|||
[[Category:Functions and mappings]] |
[[Category:Functions and mappings]] |
||
[[Category:Linear operators in calculus]] |
|||
[[Category:Rates]] |
|||
{{Link FA|de}} |
|||
[[Category:Change]] |
|||
[[af:Afgeleide]] |
|||
[[ar:اشتقاق (رياضيات)]] |
|||
[[bg:Производна]] |
|||
[[ca:Derivada]] |
|||
[[cs:Derivace]] |
|||
[[da:Differentialregning]] |
|||
[[de:Differentialrechnung]] |
|||
[[et:Tuletis (matemaatika)]] |
|||
[[es:Derivada]] |
|||
[[eo:Derivaĵo (matematiko)]] |
|||
[[eu:Deribatu]] |
|||
[[fa:مشتق]] |
|||
[[fr:Dérivée]] |
|||
[[fur:Derivade]] |
|||
[[gl:Derivada]] |
|||
[[ko:미분]] |
|||
[[io:Derivajo]] |
|||
[[id:Turunan]] |
|||
[[is:Deildun]] |
|||
[[it:Derivata]] |
|||
[[he:נגזרת]] |
|||
[[lt:Išvestinė]] |
|||
[[lmo:Derivada]] |
|||
[[hu:Differenciálhányados]] |
|||
[[mk:Диференцијално сметање]] |
|||
[[nl:Afgeleide]] |
|||
[[ja:微分法]] |
|||
[[no:Derivasjon]] |
|||
[[ug:دىففېرېنسىئال]] |
|||
[[pl:Pochodna funkcji]] |
|||
[[pt:Derivada]] |
|||
[[ro:Derivată]] |
|||
[[ru:Производная функции]] |
|||
[[sk:Derivácia (funkcia)]] |
|||
[[sr:Извод]] |
|||
[[fi:Derivaatta]] |
|||
[[sv:Derivata]] |
|||
[[th:อนุพันธ์]] |
|||
[[vi:Đạo hàm và vi phân của hàm số]] |
|||
[[tr:Türev]] |
|||
[[zh:导数]] |
|||
Latest revision as of 07:01, 15 May 2024
| Part of a series of articles about |
| Calculus |
|---|
The derivative is a fundamental tool of calculus that quantifies the sensitivity of change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable.[1] The process of finding a derivative is called differentiation.
There are multiple different notations for differentiation, two of the most commonly used being Leibniz notation and prime notation. Leibniz notation, named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas prime notation is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leibniz notation by adding superscripts to the differentials, and in prime notation by adding additional prime marks. The higher order derivatives can be applied in physics; for example, while the first derivative of the position of a moving object with respect to time is the object's velocity, how the position changes as time advances, the second derivative is the object's acceleration, how the velocity changes as time advances.
Derivatives can be generalized to functions of several real variables. In this generalization, the derivative is reinterpreted as a linear transformation whose graph is (after an appropriate translation) the best linear approximation to the graph of the original function. The Jacobian matrix is the matrix that represents this linear transformation with respect to the basis given by the choice of independent and dependent variables. It can be calculated in terms of the partial derivatives with respect to the independent variables. For a real-valued function of several variables, the Jacobian matrix reduces to the gradient vector.
Definition
As a limit
A function of a real variable is differentiable at a point of its domain, if its domain contains an open interval containing , and the limit
If the function is differentiable at , that is if the limit exists, then this limit is called the derivative of at . Multiple notations for the derivative exist.[4] The derivative of at can be denoted , read as " prime of "; or it can be denoted , read as "the derivative of with respect to at " or " by (or over) at ". See § Notation below. If is a function that has a derivative at every point in its domain, then a function can be defined by mapping every point to the value of the derivative of at . This function is written and is called the derivative function or the derivative of . The function sometimes has a derivative at most, but not all, points of its domain. The function whose value at equals whenever is defined and elsewhere is undefined is also called the derivative of . It is still a function, but its domain may be smaller than the domain of .[5]
For example, let be the squaring function: . Then the quotient in the definition of the derivative is[6]
The ratio in the definition of the derivative is the slope of the line through two points on the graph of the function , specifically the points and . As is made smaller, these points grow closer together, and the slope of this line approaches the limiting value, the slope of the tangent to the graph of at . In other words, the derivative is the slope of the tangent.[7]
Using infinitesimals
One way to think of the derivative is as the ratio of an infinitesimal change in the output of the function to an infinitesimal change in its input.[8] In order to make this intuition rigorous, a system of rules for manipulating infinitesimal quantities is required.[9] The system of hyperreal numbers is a way of treating infinite and infinitesimal quantities. The hyperreals are an extension of the real numbers that contain numbers greater than anything of the form for any finite number of terms. Such numbers are infinite, and their reciprocals are infinitesimals. The application of hyperreal numbers to the foundations of calculus is called nonstandard analysis. This provides a way to define the basic concepts of calculus such as the derivative and integral in terms of infinitesimals, thereby giving a precise meaning to the in the Leibniz notation. Thus, the derivative of becomes
Continuity and differentiability
If is differentiable at , then must also be continuous at .[11] As an example, choose a point and let be the step function that returns the value 1 for all less than , and returns a different value 10 for all greater than or equal to . The function cannot have a derivative at . If is negative, then is on the low part of the step, so the secant line from to is very steep; as tends to zero, the slope tends to infinity. If is positive, then is on the high part of the step, so the secant line from to has slope zero. Consequently, the secant lines do not approach any single slope, so the limit of the difference quotient does not exist. However, even if a function is continuous at a point, it may not be differentiable there. For example, the absolute value function given by is continuous at , but it is not differentiable there. If is positive, then the slope of the secant line from 0 to is one; if is negative, then the slope of the secant line from to is .[12] This can be seen graphically as a "kink" or a "cusp" in the graph at . Even a function with a smooth graph is not differentiable at a point where its tangent is vertical: For instance, the function given by is not differentiable at . In summary, a function that has a derivative is continuous, but there are continuous functions that do not have a derivative.[11]
Most functions that occur in practice have derivatives at all points or almost every point. Early in the history of calculus, many mathematicians assumed that a continuous function was differentiable at most points.[13] Under mild conditions (for example, if the function is a monotone or a Lipschitz function), this is true. However, in 1872, Weierstrass found the first example of a function that is continuous everywhere but differentiable nowhere. This example is now known as the Weierstrass function.[14] In 1931, Stefan Banach proved that the set of functions that have a derivative at some point is a meager set in the space of all continuous functions. Informally, this means that hardly any random continuous functions have a derivative at even one point.[15]
Notation
One common symbol for the derivative of a function is Leibniz notation. They are written as the quotient of two differentials and ,[16] which were introduced by Gottfried Wilhelm Leibniz in 1675.[17] It is still commonly used when the equation is viewed as a functional relationship between dependent and independent variables. The first derivative is denoted by , read as "the derivative of with respect to ".[18] This derivative can alternately be treated as the application of a differential operator to a function, Higher derivatives are expressed using the notation for the -th derivative of . These are abbreviations for multiple applications of the derivative operator; for example, [19] Unlike some alternatives, Leibniz notation involves explicit specification of the variable for differentiation, in the denominator, which removes ambiguity when working with multiple interrelated quantities. The derivative of a composed function can be expressed using the chain rule: if and then [20]
Another common notation for differentiation is by using the prime mark in the symbol of a function . This is known as prime notation, due to Joseph-Louis Lagrange.[21] The first derivative is written as , read as " prime of ", or , read as " prime".[22] Similarly, the second and the third derivatives can be written as and , respectively.[23] For denoting the number of higher derivatives beyond this point, some authors use Roman numerals in superscript, whereas others place the number in parentheses, such as or [24] The latter notation generalizes to yield the notation for the -th derivative of .[19]
In Newton's notation or the dot notation, a dot is placed over a symbol to represent a time derivative. If is a function of , then the first and second derivatives can be written as and , respectively. This notation is used exclusively for derivatives with respect to time or arc length. It is typically used in differential equations in physics and differential geometry.[25] However, the dot notation becomes unmanageable for high-order derivatives (of order 4 or more) and cannot deal with multiple independent variables.
Another notation is D-notation, which represents the differential operator by the symbol [19] The first derivative is written and higher derivatives are written with a superscript, so the -th derivative is This notation is sometimes called Euler notation, although it seems that Leonhard Euler did not use it, and the notation was introduced by Louis François Antoine Arbogast.[26] To indicate a partial derivative, the variable differentiated by is indicated with a subscript, for example given the function its partial derivative with respect to can be written or Higher partial derivatives can be indicated by superscripts or multiple subscripts, e.g. and .[27]
Rules of computation
In principle, the derivative of a function can be computed from the definition by considering the difference quotient and computing its limit. Once the derivatives of a few simple functions are known, the derivatives of other functions are more easily computed using rules for obtaining derivatives of more complicated functions from simpler ones. This process of finding a derivative is known as differentiation.[28]
Rules for basic functions
The following are the rules for the derivatives of the most common basic functions. Here, is a real number, and is the mathematical constant approximately 2.71828.[29]
- Derivatives of powers:
- Functions of exponential, natural logarithm, and logarithm with general base:
- , for
- , for
- , for
- Trigonometric functions:
- Inverse trigonometric functions:
- , for
- , for
Rules for combined functions
Given that the and are the functions. The following are some of the most basic rules for deducing the derivative of functions from derivatives of basic functions.[30]
- Constant rule: if is constant, then for all ,
- Sum rule:
- for all functions and and all real numbers and .
- Product rule:
- for all functions and . As a special case, this rule includes the fact whenever is a constant because by the constant rule.
- Quotient rule:
- for all functions and at all inputs where g ≠ 0.
- Chain rule for composite functions: If , then
Computation example
The derivative of the function given by is
Higher-order derivatives
Higher order derivatives means that a function is differentiated repeatedly. Given that is a differentiable function, the derivative of is the first derivative, denoted as . The derivative of is the second derivative, denoted as , and the derivative of is the third derivative, denoted as . By continuing this process, if it exists, the -th derivative as the derivative of the -th derivative or the derivative of order . As has been discussed above, the generalization of derivative of a function may be denoted as .[31] A function that has successive derivatives is called times differentiable. If the -th derivative is continuous, then the function is said to be of differentiability class .[32] A function that has infinitely many derivatives is called infinitely differentiable or smooth.[33] One example of the infinitely differentiable function is polynomial; differentiate this function repeatedly results the constant function, and the infinitely subsequent derivative of that function are all zero.[34]
In one of its applications, the higher-order derivatives may have specific interpretations in physics. Suppose that a function represents the position of an object at the time. The first derivative of that function is the velocity of an object with respect to time, the second derivative of the function is the acceleration of an object with respect to time,[28] and the third derivative is the jerk.[35]
In other dimensions
Vector-valued functions
A vector-valued function of a real variable sends real numbers to vectors in some vector space . A vector-valued function can be split up into its coordinate functions , meaning that . This includes, for example, parametric curves in or . The coordinate functions are real-valued functions, so the above definition of derivative applies to them. The derivative of is defined to be the vector, called the tangent vector, whose coordinates are the derivatives of the coordinate functions. That is,[36]
Partial derivatives
Functions can depend upon more than one variable. A partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant. Partial derivatives are used in vector calculus and differential geometry. As with ordinary derivatives, multiple notations exist: the partial derivative of a function with respect to the variable is variously denoted by
among other possibilities.[37] It can be thought of as the rate of change of the function in the -direction.[38] Here ∂ is a rounded d called the partial derivative symbol. To distinguish it from the letter d, ∂ is sometimes pronounced "der", "del", or "partial" instead of "dee".[39] For example, let , then the partial derivative of function with respect to both variables and are, respectively:
This is fundamental for the study of the functions of several real variables. Let be such a real-valued function. If all partial derivatives with respect to are defined at the point , these partial derivatives define the vector
Directional derivatives
If is a real-valued function on , then the partial derivatives of measure its variation in the direction of the coordinate axes. For example, if is a function of and , then its partial derivatives measure the variation in in the and direction. However, they do not directly measure the variation of in any other direction, such as along the diagonal line . These are measured using directional derivatives. Choose a vector , then the directional derivative of in the direction of at the point is:[42]
If all the partial derivatives of exist and are continuous at , then they determine the directional derivative of in the direction by the formula:[43]
Total derivative, total differential and Jacobian matrix
When is a function from an open subset of to , then the directional derivative of in a chosen direction is the best linear approximation to at that point and in that direction. However, when , no single directional derivative can give a complete picture of the behavior of . The total derivative gives a complete picture by considering all directions at once. That is, for any vector starting at , the linear approximation formula holds:[44]
If the total derivative exists at , then all the partial derivatives and directional derivatives of exist at , and for all , is the directional derivative of in the direction . If is written using coordinate functions, so that , then the total derivative can be expressed using the partial derivatives as a matrix. This matrix is called the Jacobian matrix of at :[46]
Generalizations
The concept of a derivative can be extended to many other settings. The common thread is that the derivative of a function at a point serves as a linear approximation of the function at that point.
- An important generalization of the derivative concerns complex functions of complex variables, such as functions from (a domain in) the complex numbers to . The notion of the derivative of such a function is obtained by replacing real variables with complex variables in the definition.[47] If is identified with by writing a complex number as , then a differentiable function from to is certainly differentiable as a function from to (in the sense that its partial derivatives all exist), but the converse is not true in general: the complex derivative only exists if the real derivative is complex linear and this imposes relations between the partial derivatives called the Cauchy–Riemann equations – see holomorphic functions.[48]
- Another generalization concerns functions between differentiable or smooth manifolds. Intuitively speaking such a manifold is a space that can be approximated near each point by a vector space called its tangent space: the prototypical example is a smooth surface in . The derivative (or differential) of a (differentiable) map between manifolds, at a point in , is then a linear map from the tangent space of at to the tangent space of at . The derivative function becomes a map between the tangent bundles of and . This definition is used in differential geometry.[49]
- Differentiation can also be defined for maps between vector space, such as Banach space, in which those generalizations are the Gateaux derivative and the Fréchet derivative.[50]
- One deficiency of the classical derivative is that very many functions are not differentiable. Nevertheless, there is a way of extending the notion of the derivative so that all continuous functions and many other functions can be differentiated using a concept known as the weak derivative. The idea is to embed the continuous functions in a larger space called the space of distributions and only require that a function is differentiable "on average".[51]
- Properties of the derivative have inspired the introduction and study of many similar objects in algebra and topology; an example is differential algebra. Here, it consists of the derivation of some topics in abstract algebra, such as rings, ideals, field, and so on.[52]
- The discrete equivalent of differentiation is finite differences. The study of differential calculus is unified with the calculus of finite differences in time scale calculus.[53]
- The arithmetic derivative involves the function that is defined for the integers by the prime factorization. This is an analogy with the product rule.[54]
See also
Notes
- ^ Stewart 2002, p. 129–130.
- ^ Stewart 2002, p. 127; Strang et al. 2023, p. 220.
- ^ Gonick 2012, p. 83.
- ^ Gonick 2012, p. 88; Strang et al. 2023, p. 234.
- ^ Gonick 2012, p. 83; Strang et al. 2023, p. 232.
- ^ Gonick 2012, pp. 77–80.
- ^ Thompson 1998, pp. 34, 104; Stewart 2002, p. 128.
- ^ Thompson 1998, pp. 84–85.
- ^ Keisler 2012, pp. 902–904.
- ^ Keisler 2012, p. 45; Henle & Kleinberg 2003, p. 66.
- ^ a b Gonick 2012, p. 156.
- ^ Gonick 2012, p. 149.
- ^ Jašek 1922; Jarník 1922; Rychlík 1923.
- ^ David 2018.
- ^ Banach 1931, cited in Hewitt & Stromberg 1965.
- ^ Apostol 1967, p. 172.
- ^ Cajori 2007, p. 204.
- ^ Moore & Siegel 2013, p. 110.
- ^ a b c Varberg, Purcell & Rigdon 2007, p. 125–126.
- ^ In the formulation of calculus in terms of limits, various authors have assigned the symbol various meanings. Some authors such as Varberg, Purcell & Rigdon 2007, p. 119 and Stewart 2002, p. 177 do not assign a meaning to by itself, but only as part of the symbol . Others define as an independent variable, and define by In non-standard analysis is defined as an infinitesimal. It is also interpreted as the exterior derivative of a function . See differential (infinitesimal) for further information.
- ^ Schwartzman 1994, p. 171.
- ^ Moore & Siegel 2013, p. 110; Goodman 1963, p. 78–79.
- ^ Varberg, Purcell & Rigdon 2007, p. 125–126; Cajori 2007, p. 228.
- ^ Choudary & Niculescu 2014, p. 222; Apostol 1967, p. 171.
- ^ Evans 1999, p. 63; Kreyszig 1991, p. 1.
- ^ Cajori 1923.
- ^ Apostol 1967, p. 172; Varberg, Purcell & Rigdon 2007, p. 125–126.
- ^ a b Apostol 1967, p. 160.
- ^ Varberg, Purcell & Rigdon 2007. See p. 133 for the power rule, p. 115–116 for the trigonometric functions, p. 326 for the natural logarithm, p. 338–339 for exponential with base , p. 343 for the exponential with base , p. 344 for the logarithm with base , and p. 369 for the inverse of trigonometric functions.
- ^ For constant rule and sum rule, see Apostol 1967, p. 161, 164, respectively. For the product rule, quotient rule, and chain rule, see Varberg, Purcell & Rigdon 2007, p. 111–112, 119, respectively. For the special case of the product rule, that is, the product of a constant and a function, see Varberg, Purcell & Rigdon 2007, p. 108–109.
- ^ Apostol 1967, p. 160; Varberg, Purcell & Rigdon 2007, p. 125–126.
- ^ Warner 1983, p. 5.
- ^ Debnath & Shah 2015, p. 40.
- ^ Carothers 2000, p. 176.
- ^ Stewart 2002, p. 193.
- ^ a b Stewart 2002, p. 893.
- ^ Stewart 2002, p. 947; Christopher 2013, p. 682.
- ^ Stewart 2002, p. 949.
- ^ Silverman 1989, p. 216; Bhardwaj 2005, See p. 6.4.
- ^ Mathai & Haubold 2017, p. 52.
- ^ Gbur 2011, pp. 36–37.
- ^ Varberg, Purcell & Rigdon 2007, p. 642.
- ^ Guzman 2003, p. 35.
- ^ a b c Davvaz 2023, p. 266.
- ^ Lee 2013, p. 72.
- ^ Davvaz 2023, p. 267.
- ^ Roussos 2014, p. 303.
- ^ Gbur 2011, pp. 261–264.
- ^ Gray, Abbena & Salamon 2006, p. 826.
- ^ Azegami 2020. See p. 209 for the Gateaux derivative, and p. 211 for the Fréchet derivative.
- ^ Funaro 1992, p. 84–85.
- ^ Kolchin 1973, p. 58, 126.
- ^ Georgiev 2018, p. 8.
- ^ Barbeau 1961.
References
- Apostol, Tom M. (June 1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra, vol. 1 (2nd ed.), Wiley, ISBN 978-0-471-00005-1
- Azegami, Hideyuki (2020), Shape Optimization Problems, Springer Optimization and Its Applications, vol. 164, Springer, doi:10.1007/978-981-15-7618-8, ISBN 978-981-15-7618-8, S2CID 226442409
- Banach, Stefan (1931), "Uber die Baire'sche Kategorie gewisser Funktionenmengen", Studia Math., 3 (3): 174–179, doi:10.4064/sm-3-1-174-179.
- Barbeau, E. J. (1961). "Remarks on an arithmetic derivative". Canadian Mathematical Bulletin. 4 (2): 117–122. doi:10.4153/CMB-1961-013-0. Zbl 0101.03702.
- Bhardwaj, R. S. (2005), Mathematics for Economics & Business (2nd ed.), Excel Books India, ISBN 9788174464507
- Cajori, Florian (1923), "The History of Notations of the Calculus", Annals of Mathematics, 25 (1): 1–46, doi:10.2307/1967725, hdl:2027/mdp.39015017345896, JSTOR 1967725
- Cajori, Florian (2007), A History of Mathematical Notations, vol. 2, Cosimo Classics, ISBN 978-1-60206-713-4
- Carothers, N. L. (2000), Real Analysis, Cambridge University Press
- Choudary, A. D. R.; Niculescu, Constantin P. (2014), Real Analysis on Intervals, Springer India, doi:10.1007/978-81-322-2148-7, ISBN 978-81-322-2148-7
- Christopher, Essex (2013), Calculus: A complete course, Pearson, p. 682, ISBN 9780321781079, OCLC 872345701
- Courant, Richard; John, Fritz (December 22, 1998), Introduction to Calculus and Analysis, Vol. 1, Springer-Verlag, doi:10.1007/978-1-4613-8955-2, ISBN 978-3-540-65058-4
- David, Claire (2018), "Bypassing dynamical systems: A simple way to get the box-counting dimension of the graph of the Weierstrass function", Proceedings of the International Geometry Center, 11 (2), Academy of Sciences of Ukraine: 53–68, arXiv:1711.10349, doi:10.15673/tmgc.v11i2.1028
- Davvaz, Bijan (2023), Vectors and Functions of Several Variables, Springer, doi:10.1007/978-981-99-2935-1, ISBN 978-981-99-2935-1, S2CID 259885793
- Debnath, Lokenath; Shah, Firdous Ahmad (2015), Wavelet Transforms and Their Applications (2nd ed.), Birkhäuser, doi:10.1007/978-0-8176-8418-1, ISBN 978-0-8176-8418-1
- Evans, Lawrence (1999), Partial Differential Equations, American Mathematical Society, ISBN 0-8218-0772-2
- Eves, Howard (January 2, 1990), An Introduction to the History of Mathematics (6th ed.), Brooks Cole, ISBN 978-0-03-029558-4
- Funaro, Daniele (1992), Polynomial Approximation of Differential Equations, Lecture Notes in Physics Monographs, vol. 8, Springer, doi:10.1007/978-3-540-46783-0, ISBN 978-3-540-46783-0
- Gbur, Greg (2011), Mathematical Methods for Optical Physics and Engineering, Cambridge University Press, Bibcode:2011mmop.book.....G, ISBN 978-1-139-49269-0
- Georgiev, Svetlin G. (2018), Fractional Dynamic Calculus and Fractional Dynamic Equations on Time Scales, Springer, doi:10.1007/978-3-319-73954-0, ISBN 978-3-319-73954-0
- Goodman, A. W. (1963), Analytic Geometry and the Calculus, The MacMillan Company
- Gonick, Larry (2012), The Cartoon Guide to Calculus, William Morrow, ISBN 978-0-06-168909-3
- Gray, Alfred; Abbena, Elsa; Salamon, Simon (2006), Modern Differential Geometry of Curves and Surfaces with Mathematica, CRC Press, ISBN 978-1-58488-448-4
- Guzman, Alberto (2003), Derivatives and Integrals of Multivariable Functions, Springer, doi:10.1007/978-1-4612-0035-2, ISBN 978-1-4612-0035-2
- Henle, James M.; Kleinberg, Eugene M. (2003), Infinitesimal Calculus, Dover Publications, ISBN 978-0-486-42886-4
- Hewitt, Edwin; Stromberg, Karl R. (1965), Real and abstract analysis, Springer-Verlag, Theorem 17.8, doi:10.1007/978-3-662-29794-0, ISBN 978-3-662-28275-5
- Jašek, Martin (1922), "Funkce Bolzanova" (PDF), Časopis pro Pěstování Matematiky a Fyziky (in Czech), 51 (2): 69–76, doi:10.21136/CPMF.1922.121916
- Jarník, Vojtěch (1922), "O funkci Bolzanově" (PDF), Časopis pro Pěstování Matematiky a Fyziky (in Czech), 51 (4): 248–264, doi:10.21136/CPMF.1922.109021. See the English version here.
- Keisler, H. Jerome (2012) [1986], Elementary Calculus: An Approach Using Infinitesimals (2nd ed.), Prindle, Weber & Schmidt, ISBN 978-0-871-50911-6
- Kolchin, Ellis (1973), Differential Algebra And Algebraic Groups, Academic Press, ISBN 978-0-08-087369-5
- Kreyszig, Erwin (1991), Differential Geometry, New York: Dover, ISBN 0-486-66721-9
- Larson, Ron; Hostetler, Robert P.; Edwards, Bruce H. (February 28, 2006), Calculus: Early Transcendental Functions (4th ed.), Houghton Mifflin Company, ISBN 978-0-618-60624-5
- Lee, John M. (2013), Introduction to Smooth Manifolds, Graduate Texts in Mathematics, vol. 218, Springer, doi:10.1007/978-0-387-21752-9, ISBN 978-0-387-21752-9
- Mathai, A. M.; Haubold, H. J. (2017), Fractional and Multivariable Calculus: Model Building and Optimization Problems, Springer, doi:10.1007/978-3-319-59993-9, ISBN 978-3-319-59993-9
- Moore, Will H.; Siegel, David A. (2013), A Mathematical Course for Political and Social Research, Princeton University Press, ISBN 978-0-691-15995-9
- Roussos, Ioannis M. (2014), Improper Riemann Integral, CRC Press, ISBN 978-1-4665-8807-3
- Rychlík, Karel (1923), Über eine Funktion aus Bolzanos handschriftlichem Nachlasse
- Schwartzman, Steven (1994), The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English, Mathematical Association of American, ISBN 9781614445012
- Silverman, Richard A. (1989), Essential Calculus: With Applications, Courier Corporation, ISBN 9780486660974
- Stewart, James (December 24, 2002), Calculus (5th ed.), Brooks Cole, ISBN 978-0-534-39339-7
- Strang, Gilbert; et al. (2023), Calculus, volume 1, OpenStax, ISBN 978-1-947172-13-5
- Thompson, Silvanus P. (September 8, 1998), Calculus Made Easy (Revised, Updated, Expanded ed.), New York: St. Martin's Press, ISBN 978-0-312-18548-0
- Varberg, Dale E.; Purcell, Edwin J.; Rigdon, Steven E. (2007), Calculus (9th ed.), Pearson Prentice Hall, ISBN 978-0131469686
- Warner, Frank W. (1983), Foundations of Differentiable Manifolds and Lie Groups, Springer, ISBN 978-0-387-90894-6
External links
- "Derivative", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Khan Academy: "Newton, Leibniz, and Usain Bolt"
- Weisstein, Eric W. "Derivative". MathWorld.
- Online Derivative Calculator from Wolfram Alpha.