Champernowne number

The Champernowne number is a real number from the field of number theory . It is named after the mathematician David Gawen Champernowne , who in 1933 published the explicit construction of a normal number for the first time . The decimal sequence of digits is the sequence A033307 in OEIS . Kurt Mahler showed in 1937 that this is a transcendent number .

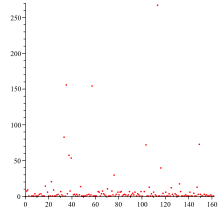
The first 161 quotients of the continued fraction. The 4th, 18th, 40th and 101st positions are missing because they are very large in terms of value.

It is formed by “lining up” the natural numbers as decimal places. There is a zero in front of the comma.

In the decimal system, the first digits of the Champernowne number are:

${\displaystyle C_{10}=0{,}12345678910111213141516\ldots }$

It can also be expressed as a series:

${\displaystyle C_{10}=\sum _{n=1}^{\infty }\sum _{k=10^{n-1}}^{10^{n}-1}{\frac {k}{10^{kn-9\sum _{j=0}^{n-1}10^{j}(n-j-1)}}}}$

Representation as an infinite continued fraction

As already mentioned, the Champernowne number is transcendent. Because it is not a rational number , the continued fraction that represents this number is an infinite continued fraction . In addition, because it is not a quadratic irrational number , the infinite continued fraction is also not periodic . The representation of the Champernowne number as an infinite continued fraction shows large jumps in the sequence of the quotients in the decimal system, where several very small quotients are followed by very large ones. It is: ${\displaystyle C_{10}}$ ${\displaystyle C_{10}}$ ${\displaystyle C_{10}}$ ${\displaystyle C_{10}}$

${\displaystyle C_{10}=0+{\frac {1}{8+{\frac {1}{9+{\frac {1}{1+{\frac {1}{149083+\ldots }}}}}}}}}$

Written in the usual mathematical notation for regular continued fractions, the continued fraction expansion is:

${\displaystyle C_{10}=[0;8,9,1,149083,1,1,1,4,1,1,1,3,4,1,1,1,15,4575401113910310764836466282429561185996039397104575550006620043930902626592563149379532077471286563138641209375503552094607183089984575801469863148833592141783010987,6,1,1,21,1,9,1,1,2,3,1,7,2,1,83,1,156,4,58,8,54,\ldots ]}$(Follow A030167 in OEIS )

You can see that the value in the 19th position has 166 places. The next very large value can be found in the continued fraction at the 41st position and has 2504 digits. Since continued fractions are used primarily to "good convergents" for irrational numbers to find (and any transcendental number is also irrational), these large values mean in the continued fraction development that the champernowne constant can approximate well extremely, if you before this large values. That means, if you break off the continued fraction at the 4th position (i.e. before the value 149083), you get for the approximate fractions: ${\displaystyle C_{10}}$

${\displaystyle C_{10}\approx [0;8,9,1]=0+{\frac {1}{8+{\frac {1}{9+{\frac {1}{1}}}}}}={\frac {10}{81}}=0{,}{\overline {123456790}}}$

This approximate fraction already corresponds to the Champernowne number to 9 places after the decimal point. If you break off the continued fraction at the 18th position (i.e. before the 166-digit value at the 19th position), you get for the approximate fractions: ${\displaystyle C_{10}}$

${\displaystyle C_{10}\approx [0;8,9,1,149083,1,1,1,4,1,1,1,3,4,1,1,1,15]={\frac {60499999499}{490050000000}}=0{,}123456789{\overline {101112\ldots 96979900010203040506070809}}}$

This approximate fraction already corresponds to the Champernowne number to 186 places after the decimal point. ${\displaystyle C_{10}}$

generalization

If you cut off the Champernowne number at the -th place after the decimal point and turn it into a whole number, you get the following number: ${\displaystyle C_{10}}$ ${\displaystyle n}$

${\displaystyle a_{n}=\lfloor C_{10}\cdot 10^{n}\rfloor }$

The first numbers you get are the following:

1, 12, 123, 1234, 12345, 123456 , 1234567, 12345678, 123456789, 1234567891, 12345678910, 123456789101, 1234567891011, 12345678910111, 123456789101112, 1234567891011121, ... ( continuation A252043 in OEIS )

If such a number is a prime number, it is called a Champernowne prime number .

The first Champernowne primes are as follows:

1234567891, 12345678910111, 123456789101112131415161, ... (Follow A176942 in OEIS )

The number of digits of the first Champernowne prime numbers are as follows:

10, 14, 24, 235, 2804, 4347, 37735,… (Follow A071620 in OEIS )

The eighth (not yet discovered) Champernowne prime will have more than 37,800 digits.

See also

• Smarandache Wellin Number

Web links

• Eric W. Weisstein : Champernowne constant . In: MathWorld (English).

Individual evidence

1. ^ DG Champernowne: The Construction of Decimals Normal in the Scale of Ten. J. London Math. Soc. 8, 1933.
2. ↑ Kurt Mahler : Arithmetic properties of a class of decimal fractions . (PDF) In: Proc. Konin. Neder. Akad. Wet. Ser. A. , 40, 1937, pp. 421-428
3. ↑ Eric W. Weisstein : Smarandache Prime . In: MathWorld (English).
4. ↑ Neil Sloane : Champernowne primes - Comments. OEIS , accessed August 3, 2018 .