Extended real number

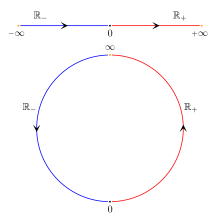
Two different methods of extending real numbers by infinity

In mathematics, an extended real number is a set that is created from the body of real numbers by adding new symbols for infinite elements (also: improper points ). A more precise distinction is made between the affinely extended real numbers , in which there are two unsigned improper points, and the projectively extended real numbers with only one unsigned improper point. Without the addition of affine or projective , the term extended real numbers is usually used synonymously with affine extended real numbers in the literature , but in this article this is used as a common generic term for both extensions.

For example, the affinely extended real numbers make it possible to view the infinite elements as the limit value of certain divergent sequences and thus to treat such sequences analogously to convergent sequences. The definition of the extensions is accordingly initially topologically motivated. The arithmetic of the real numbers, on the other hand, cannot be fully extended to the extended real numbers.

definition

With their usual topology, the real numbers form a locally compact space. By appropriately adding improper points, this creates a compact space .

• In the affine extension, two elements are added and signed infinities are added . At first, any two non-elements of the real numbers are simply referred to. ${\displaystyle \mathbb {R} }$ ${\displaystyle +\infty }$ ${\displaystyle -\infty }$ ${\displaystyle {\bar {\mathbb {R} }}:=\mathbb {R} \cup \{+\infty ,-\infty \}}$ ${\displaystyle \pm \infty }$
• In the case of projective expansion, consider one- point compactification with a single improper point indicated by the symbol . ${\displaystyle \mathbb {R} ^{\ast }:=\mathbb {R} \cup \{\infty \}}$ ${\displaystyle \infty }$

topology

Every in open set is also in or open. In addition, an environment base is given for the improper points. ${\displaystyle \mathbb {R} }$ ${\displaystyle {\bar {\mathbb {R} }}}$ ${\displaystyle \mathbb {R} ^{\ast }}$

Affine case

For each should ${\displaystyle a\in \mathbb {R} }$

${\displaystyle \left[-\infty ,a\right[:=\{x\in \mathbb {R} \mid x<a\}\cup \{-\infty \}}$

an open environment of and ${\displaystyle -\infty }$

${\displaystyle \left]a,+\infty \right]:=\{x\in \mathbb {R} \mid x>a\}\cup \{+\infty \}}$

an open environment of being. In this way, for example, the sequence given by becomes a counter- convergent sequence: for each , almost all sequence members are contained in, namely all those with . ${\displaystyle +\infty }$ ${\displaystyle x_{n}=n}$ ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ ${\displaystyle +\infty }$ ${\displaystyle a\in \mathbb {R} }$ ${\displaystyle ]a,+\infty ]}$ ${\displaystyle n>a}$

The figure that by ${\displaystyle f\colon {\bar {\mathbb {R} }}\to [-1,1]}$

${\displaystyle f(x)={\frac {x}{1+|x|}}}$for , , ${\displaystyle x\in \mathbb {R} }$ ${\displaystyle f(-\infty )=-1}$ ${\displaystyle f(+\infty )=+1}$

is given is a homeomorphism . Topologically is therefore completely equivalent to a closed interval. ${\displaystyle {\bar {\mathbb {R} }}}$

The affine extended real numbers form a strictly total ordered set, in that the order of the real numbers is continued through , for all and . The usual notations for open, and for half-open and for closed intervals are therefore also useful if and / or is. The topology of is also defined by this order order topology . ${\displaystyle -\infty <a}$ ${\displaystyle a<+\infty }$ ${\displaystyle a\in \mathbb {R} }$ ${\displaystyle -\infty <+\infty }$ ${\displaystyle ]a,b[}$ ${\displaystyle [a,b[}$ ${\displaystyle ]a,b]}$ ${\displaystyle [a,b]}$ ${\displaystyle a=-\infty }$ ${\displaystyle b=+\infty }$ ${\displaystyle {\bar {\mathbb {R} }}}$

Homeomorphism with shows that it is metrizable . However, the standard metric on cannot be continued into a metric on : this would have to be open, i.e. contain a; but this would result ${\displaystyle [-1,1]}$ ${\displaystyle {\bar {\mathbb {R} }}}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle {\bar {\mathbb {R} }}}$ ${\displaystyle \{x\in {\bar {\mathbb {R} }}\mid d(x,+\infty )<1\}}$ ${\displaystyle ]a,+\infty ]}$

${\displaystyle 2=d(a+1,a+3)\leq d(a+1,+\infty )+d(+\infty ,a+3)<1+1}$

consequences.

Projective case

For every positive real number, let the complement of the open neighborhood of be. More generally, it follows, as is usual for one-point compactification, that for every compact subset the complement is an open neighborhood of . As a result, for example, the sequence given by becomes a counter- convergent sequence: For each , almost all sequence members are contained in the complement of , i.e. H. it applies . In general, every real sequence that is definitely divergent in terms of its magnitude becomes one that is convergent towards . ${\displaystyle r}$ ${\displaystyle [-r,r]}$ ${\displaystyle \infty }$ ${\displaystyle K\subset \mathbb {R} }$ ${\displaystyle \mathbb {R} ^{\ast }\setminus K}$ ${\displaystyle \infty }$ ${\displaystyle x_{n}=(-1)^{n}n}$ ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ ${\displaystyle \infty }$ ${\displaystyle r>0}$ ${\displaystyle [-r,r]}$ ${\displaystyle |x_{n}|>r}$ ${\displaystyle \mathbb {R} ^{\ast }}$ ${\displaystyle \infty }$

With this topology homeomorphic becomes a circular line ${\displaystyle \mathbb {R} ^{\ast }}$

${\displaystyle S^{1}=\{(x,y)\in \mathbb {R} ^{2}\mid x^{2}+y^{2}=1\}.}$

A homeomorphism is given by, for example ${\displaystyle g\colon S^{1}\to \mathbb {R} ^{\ast }}$

${\displaystyle g(x,y)={\frac {x}{1-y}}}$for and . ${\displaystyle (x,y)\neq (0,1)}$ ${\displaystyle g(0,1)=\infty }$

Just like the circular line, it cannot be totally ordered in a way that is compatible with the topology. Usually one leaves it at that that is incomparable with finite numbers. ${\displaystyle \mathbb {R} ^{\ast }}$ ${\displaystyle \infty }$

As in the affine case, the projective extension can also be metrised, but not by continuing the real standard metric.

One can also called out by gluing together the points and thinking emerged. ${\displaystyle \mathbb {R} ^{\ast }}$ ${\displaystyle {\bar {\mathbb {R} }}}$ ${\displaystyle -\infty }$ ${\displaystyle +\infty }$

In addition, it corresponds to the real projective straight line , which also motivates the designation. ${\displaystyle \mathbb {R} ^{\ast }}$ ${\displaystyle \mathbb {R} P^{1}}$

Common characteristics

Both affine and projective expansion form a compact space in which the real numbers are a dense subset . It follows from this that every sequence of numbers then contains a convergent partial sequence (even if it is against an improper point). Only real sequences that are determined or determined in terms of amount become convergent sequences in the affine or projective expansion. A sequence like the one given by is also divergent in the expanded real numbers. In the Stone-Čech compactification of the real numbers, on the other hand, all bounded sequences converge. ${\displaystyle x_{n}=(-1)^{n}}$

Simplified notations

The introduction of the (affine) extended real numbers initially allows to treat the spellings and analogously to finite , without introducing this separately as a separate notation or way of speaking. Even in any case, only symbolic spellings such as for certain divergent sequences are seamlessly integrated into the case of convergent sequences. ${\displaystyle \lim _{x\to +\infty }}$ ${\displaystyle \lim _{x\to -\infty }}$ ${\displaystyle \lim _{x\to x_{0}}}$ ${\displaystyle x_{0}}$ ${\displaystyle \lim x_{n}=+\infty }$

arithmetic

The question arises as to how the basic mathematical arithmetic operations should be adapted to the new infinite places. In the sense of the principle of permanence , old rules of calculation should continue to exist, but this is not universally feasible, since the expanded real numbers cannot form a completely ordered field - such a field would have to be isomorphic (and homeomorphic) again . The operations remain undefined for at least some arguments. ${\displaystyle \mathbb {R} }$

For or one would like a value for the expressions that is in turn in for as many as possible ${\displaystyle A={\bar {\mathbb {R} }}}$ ${\displaystyle A=\mathbb {R} ^{\ast }}$ ${\displaystyle a,b\in A}$ ${\displaystyle A}$

${\displaystyle a+b,\quad -a,\quad a-b,\quad a\cdot b,\quad a^{-1},\quad {\frac {a}{b}}}$

Define in such a way that the usual laws of calculation (especially associative law and commutative law of addition and multiplication as well as the distributive law ) also remain valid for this extension. More precisely, a meaningful requirement reads: If two expressions in a finite number of variables always match in the finite, provided that both sides (i.e. also all partial expressions used) are defined, and if one side is not always undefined for trivial reasons, then this equality of the two expressions should be also apply in the extension, i.e. if infinite values ​​are permitted for the variables and all subexpressions are defined. One such equation is, for example . In the finite sense this applies to , i. H. as soon as and are defined (the product is always defined here). If the extension is defined for the case , either must apply or the product must be undefined. ${\displaystyle {\tfrac {a}{b}}\cdot {\tfrac {b}{a}}=1}$ ${\displaystyle a\neq 0,b\neq 0}$ ${\displaystyle {\tfrac {a}{b}}}$ ${\displaystyle {\tfrac {b}{a}}}$ ${\displaystyle a=1,b=0}$ ${\displaystyle {\tfrac {1}{0}}=\infty }$ ${\displaystyle \infty \cdot 0={\tfrac {1}{0}}\cdot {\tfrac {0}{1}}=1}$ ${\displaystyle \infty \cdot 0}$

In addition to the basic arithmetic operations, the power calculation is also of interest . H. you want the expression for as many assign a value so that the power laws , , always be true if all subexpressions occur are defined. ${\displaystyle a^{b}}$ ${\displaystyle a,b}$ ${\displaystyle a^{b+c}=a^{b}\cdot a^{c}}$ ${\displaystyle a^{b\cdot c}=(a^{b})^{c}}$ ${\displaystyle (a\cdot b)^{c}=a^{c}\cdot b^{c}}$

Calculation rules based on continuity

The mentioned (algebraically formulated) conditions are fulfilled in any case if the operations are continuously continued. However, there is, for example, no continuous mapping or that corresponds to the addition. Therefore, continuous continuation is only partially possible. Continuous continuation as far as possible results in the following calculation rules, in which the value "?" Is noted for expressions that cannot be defined in this way: ${\displaystyle {\bar {\mathbb {R} }}\times {\bar {\mathbb {R} }}\to {\bar {\mathbb {R} }}}$ ${\displaystyle \mathbb {R} ^{\ast }\times \mathbb {R} ^{\ast }\to \mathbb {R} ^{\ast }}$ ${\displaystyle \mathbb {R} \times \mathbb {R} }$

Basic arithmetic

in ${\displaystyle {\bar {\mathbb {R} }}}$	in ${\displaystyle \mathbb {R} ^{\ast }}$
Comparisons
${\displaystyle -\infty <a<+\infty }$ for finite ${\displaystyle a}$	${\displaystyle \infty }$can not be compared with finite ${\displaystyle a}$
negation
${\displaystyle -(\pm \infty )=\mp \infty }$	${\displaystyle -\infty =\infty }$
Addition and subtraction
${\displaystyle \pm \infty +a=a\pm \infty =\pm \infty }$ for finite ${\displaystyle a}$ ${\displaystyle \infty +\infty =\infty }$ ${\displaystyle -\infty -\infty =-\infty }$	${\displaystyle \infty +a=a+\infty =\infty }$ for finite ${\displaystyle a}$
${\displaystyle \infty -\infty =?}$	${\displaystyle \infty \pm \infty =?}$
multiplication
${\displaystyle (\pm \infty )\cdot a=a\cdot (\pm \infty )=\pm \infty }$ For ${\displaystyle 0<a\leq \infty }$ ${\displaystyle (\pm \infty )\cdot a=a\cdot (\pm \infty )=\mp \infty }$ For ${\displaystyle -\infty \leq a<0}$	${\displaystyle \infty \cdot a=a\cdot \infty =\infty }$for (inclusive ) ${\displaystyle a\neq 0}$ ${\displaystyle a=\infty }$
${\displaystyle 0\cdot (\pm \infty )=0}$	${\displaystyle 0\cdot \infty =?}$
Reciprocals
${\displaystyle (\pm \infty )^{-1}=0}$	${\displaystyle \infty ^{-1}=0}$
${\displaystyle 0^{-1}=?}$	${\displaystyle 0^{-1}=\infty }$
division
${\displaystyle {\tfrac {a}{\pm \infty }}=0}$ for finite ${\displaystyle a}$ ${\displaystyle {\tfrac {\pm \infty }{a}}=\pm \infty }$ For ${\displaystyle 0<a<\infty }$ ${\displaystyle {\tfrac {\pm \infty }{a}}=\mp \infty }$ For ${\displaystyle -\infty <a<0}$	${\displaystyle {\tfrac {a}{\infty }}=0}$ for finite ${\displaystyle a}$ ${\displaystyle {\tfrac {\infty }{a}}=\infty }$ for finite ${\displaystyle a}$ ${\displaystyle {\tfrac {a}{0}}=\infty }$ For ${\displaystyle 0\neq a\neq \infty }$
${\displaystyle {\tfrac {\infty }{\infty }}=?}$ ${\displaystyle {\tfrac {a}{0}}=?}$for any ${\displaystyle a}$	${\displaystyle {\tfrac {\infty }{\infty }}=?}$ ${\displaystyle {\tfrac {0}{0}}=?}$

Potencies

Domain (red) of in the real and candidates (blue) for continuous continuations. The infinitely long axes are compressed to a finite interval, with zero in the middle. ${\displaystyle x^{y}}$

In the following, the continuous continuation of the exponentiation is given only in the affine case . It should be noted that the finite is only (real) defined if (and any) or and or and . ${\displaystyle {\bar {\mathbb {R} }}=\mathbb {R} \cup \{-\infty ,+\infty \}}$ ${\displaystyle a^{b}}$ ${\displaystyle a>0}$ ${\displaystyle b}$ ${\displaystyle a<0}$ ${\displaystyle b\in \mathbb {Z} }$ ${\displaystyle a=0}$ ${\displaystyle b\geq 0}$

Expression	value	condition
${\displaystyle a^{+\infty }}$	${\displaystyle +\infty }$	${\displaystyle 1<a\leq +\infty }$
	${\displaystyle 0}$	${\displaystyle -1<a<1}$
	?	${\displaystyle a=1}$ or ${\displaystyle -\infty \leq a\leq -1}$
${\displaystyle a^{-\infty }}$	${\displaystyle 0}$	${\displaystyle 1<a\leq +\infty }$ or ${\displaystyle -\infty \leq a<-1}$
	${\displaystyle +\infty }$	${\displaystyle 0\leq a<1}$
	?	${\displaystyle -1\leq a<0}$
${\displaystyle 0^{a}}$	${\displaystyle +\infty }$	${\displaystyle -\infty \leq a<0}$and is not an odd integer ${\displaystyle a}$
	?	${\displaystyle a}$ is a negative odd integer
	?	${\displaystyle a=+\infty }$
${\displaystyle (+\infty )^{a}}$	${\displaystyle +\infty }$	${\displaystyle 0<a\leq +\infty }$
	${\displaystyle 0}$	${\displaystyle -\infty \leq a<0}$
	?	${\displaystyle a=0}$
${\displaystyle (-\infty )^{n}}$	${\displaystyle (-1)^{n}\infty }$	${\displaystyle n>0}$ integer
	${\displaystyle 1}$	${\displaystyle n=0}$
	${\displaystyle 0}$	${\displaystyle n<0}$ and integer

The value of with negative and finite not-whole remains undefined, since these places do not belong to the end of the domain of definition of the finite power function. Regarding the continuous continuations with a non-positive basis , it should be noted that although these passages belong to the conclusion of the domain of definition, they are not internal points of the conclusion. There are therefore consequences that are completely outside the domain of definition and that converge against these passages. ${\displaystyle a^{b}}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle -\infty \leq a\leq 0}$

Function values

Some standard functions can be continuously extended into infinity to form images , for example ${\displaystyle {\bar {\mathbb {R} }}\to {\bar {\mathbb {R} }}}$

• ${\displaystyle |\pm \infty |=+\infty }$
• ${\displaystyle \arctan(\pm \infty ):=\pm {\frac {\pi }{2}}}$
• ${\displaystyle e^{+\infty }:=+\infty }$and (however, in is not defined). ${\displaystyle e^{-\infty }:=0}$ ${\displaystyle \mathbb {R} ^{\ast }}$ ${\displaystyle e^{\infty }}$

In measure theory, a function with a non-empty set is called numeric . Numerical functions can appear as the supremum or infimum of a sequence of real functions. The function values ​​are also allowed in the optimization partly for practical reasons . Functions that take on these values ​​are called extended functions . ${\displaystyle f\colon \Omega \to {\bar {\mathbb {R} }}}$ ${\displaystyle \Omega }$ ${\displaystyle \pm \infty }$

Undefined expressions

With the method of the continuous continuation one can use expressions for the basic calculation types ${\displaystyle {\bar {\mathbb {R} }}}$

${\displaystyle \infty -\infty ,\quad 0\cdot \infty ,\quad {\frac {\infty }{\infty }},\quad {\frac {a}{0}}}$

or in for ${\displaystyle \mathbb {R} ^{\ast }}$

${\displaystyle \quad \infty +\infty ,\quad 0\cdot \infty ,\quad {\frac {\infty }{\infty }},\quad {\frac {0}{0}}}$

do not specify a value. In principle it would be conceivable to find a suitable - necessarily discontinuous - setting. However, this is not possible for the expressions mentioned without violating the principle of permanence, i.e. H. without contradicting the usual rules of calculation. This is shown in detail in the following list:

• ${\displaystyle \infty -\infty }$:

  Because for all, it follows from the principle of permanence that should apply when the term is defined. However, this leads to the contradiction . ${\displaystyle x-x=0}$ ${\displaystyle x\in \mathbb {R} }$ ${\displaystyle \infty -\infty =0}$ ${\displaystyle \infty =\infty +0=\infty +(\infty -\infty )=(\infty +\infty )-\infty =\infty -\infty =0}$

• ${\displaystyle \infty +\infty }$in : ${\displaystyle \mathbb {R} ^{\ast }}$

  Analog, there . ${\displaystyle \infty =-\infty }$

• ${\displaystyle 0\cdot \infty }$:

  Because for everyone should apply. On the other hand , if the left side is defined. Hence the contradiction arises ${\displaystyle 0\cdot x=0}$ ${\displaystyle x\in \mathbb {R} }$ ${\displaystyle 0\cdot \infty =0}$ ${\displaystyle x^{-1}\cdot x=1}$ ${\displaystyle 0=0\cdot \infty =\infty ^{-1}\cdot \infty =1}$

• ${\displaystyle {\frac {\infty }{\infty }}}$:

  Because of and results ${\displaystyle {\tfrac {x}{x}}=1}$ ${\displaystyle {\tfrac {2x}{x}}=2}$ ${\displaystyle 1={\tfrac {\infty }{\infty }}={\tfrac {2\infty }{\infty }}=2}$

• ${\displaystyle {\frac {0}{0}}}$:

  Here too follows . ${\displaystyle 1={\tfrac {0}{0}}={\tfrac {2\cdot 0}{0}}=2}$

• ${\displaystyle {\frac {a}{0}}}$in : ${\displaystyle {\bar {\mathbb {R} }}}$

  From it follows that should apply, consequently . Because follows . ${\displaystyle {\tfrac {x}{y}}=-{\tfrac {x}{-y}}}$ ${\displaystyle {\tfrac {a}{0}}=-{\tfrac {a}{0}}}$ ${\displaystyle {\tfrac {a}{0}}=0}$ ${\displaystyle {\tfrac {x}{y}}\cdot {\tfrac {y}{x}}=1}$ ${\displaystyle 0=0\cdot 0={\tfrac {a}{0}}\cdot {\tfrac {0}{a}}=1}$

Assigning a value to the expressions listed is therefore not possible in a “reasonable” way. Apart from with , the expressions not defined in this way are also referred to as indeterminate expressions , for which it is nevertheless possible in certain individual cases to calculate valid numerical values using the de l'Hospital rule. ${\displaystyle {\tfrac {a}{0}}}$ ${\displaystyle a\neq 0}$ ${\displaystyle {\bar {\mathbb {R} }}}$

Deviating from the above list, it is usually agreed in some areas of mathematics, namely in measure theory , since in this way numerous statements can be made more concise. In this case it must be ensured that the reciprocal value of infinity is never used, or the determination is to be dispensed with. Otherwise, the exceptions to the usual calculation rules (namely that it does not always apply) would have to be considered regularly by case distinctions, and this made up for the advantage of the abbreviation. ${\displaystyle 0\cdot \infty =0}$ ${\displaystyle \infty ^{-1}=0}$ ${\displaystyle x\cdot x^{-1}=1}$

Algebraic continuation of exponentiation

In contrast to the four basic arithmetic operations, it is also possible, regardless of continuity considerations, to be consistent (but discontinuous)

${\displaystyle 1^{\pm \infty }=(\pm \infty )^{0}=1}$

define. The fact that at least no other value can be defined for these expressions results directly from the principle of permanence, since it applies in the finite . These determinations are consistent in the sense that the power laws , and apply whenever all subexpressions are defined. ${\displaystyle 1^{x}=x^{0}=1}$ ${\displaystyle a^{b}\cdot a^{c}=a^{b+c}}$ ${\displaystyle (a\cdot b)^{c}=a^{c}\cdot b^{c}}$ ${\displaystyle (a^{b})^{c}=a^{b\cdot c}}$

In connection with limit value investigations, however, the expressions , and are counted among the indefinite expressions, since continuity is decisive in this context. In certain individual cases, however, it is also possible here to use de l'Hospital's rule for the above Expressions calculate valid numerical values. ${\displaystyle 1^{\infty }}$ ${\displaystyle \infty ^{0}}$ ${\displaystyle 0^{0}}$

Solving equations

Care should be taken in solving equations when working with infinities, as additional solutions may exist. This becomes particularly obvious with the equation , which always has exactly one solution for finite values. On the other hand has none and an infinite number. The following table shows some further examples that result from the calculation rules above: ${\displaystyle a+x=b}$ ${\displaystyle a,b}$ ${\displaystyle \infty +x=0}$ ${\displaystyle \infty +x=\infty }$

equation	Solutions in ${\displaystyle \mathbb {R} }$	Additionally in ${\displaystyle {\bar {\mathbb {R} }}}$	Additionally in ${\displaystyle \mathbb {R} ^{\ast }}$
${\displaystyle x=-x}$	${\displaystyle 0}$		${\displaystyle \infty }$
${\displaystyle x=2x}$	${\displaystyle 0}$	${\displaystyle +\infty ,-\infty }$	${\displaystyle \infty }$
${\displaystyle x=x\cdot x}$	${\displaystyle 0,1}$	${\displaystyle +\infty }$	${\displaystyle \infty }$

When reshaping equations, the abbreviation property of addition (from follows ) can no longer be used in general , but only under the condition that is finite. The abbreviation property of multiplication (from follows ), which also applies in the finite only on condition , is also invalid for the infinite . The last equation from the table above,, cannot be transformed in an equivalent manner , because, in contrast to the former, it does not have an infinite solution ( the right-hand side is not defined for). ${\displaystyle a+c=b+c}$ ${\displaystyle a=b}$ ${\displaystyle c}$ ${\displaystyle a\cdot c=b\cdot c}$ ${\displaystyle a=b}$ ${\displaystyle c\neq 0}$ ${\displaystyle c}$ ${\displaystyle x=x\cdot x}$ ${\displaystyle 0=x\cdot x-x}$ ${\displaystyle x=+\infty }$

Complex numbers

If one starts from the complex numbers instead of the real ones, one mainly considers the single-point compactification homeomorphic to a sphere ( Riemann number sphere ). The calculation rules for the basic arithmetic operations essentially agree with those for the one-point compactification of . Here, too, there are alternative approaches in which a closed circular disk or a projective plane is compacted. ${\displaystyle \mathbb {C} }$ ${\displaystyle S^{2}}$ ${\displaystyle \mathbb {C} ^{\ast }:=\mathbb {C} \cup \{\infty \}}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$

Individual evidence

1. ↑ konzis (entry "konzis" in the Wiktionary)
2. ↑ Wolfram Alpha delivers indeterminates as the result of (input: 1 ^ Infinity ), on the other hand 1 for (input: prod_ {n = 1} ^ Infinity 1 ). ${\displaystyle 1^{\infty }}$ ${\displaystyle \prod _{n=1}^{\infty }1}$

Web links

• Davic W. Cantrell: Affinely Extended Real Numbers. In: MathWorld . Wolfram Research Inc., accessed July 27, 2010 . 
• Davic W. Cantrell: Projectively Extended Real Numbers. In: MathWorld. Wolfram Research Inc., accessed July 27, 2010 .