Congruence (geometry)

In geometry , two figures are congruent (congruent or uniform) (from the Latin congruens = corresponding, matching) if they can be converted into one another by means of a congruence mapping . Congruence maps (also called movements ) are parallel displacement , rotation , mirroring and the links between these maps.

The congruence of two flat geometric figures can be clearly interpreted as follows: You can cut out one figure with scissors and place it on top of the other so that both are exactly on top of each other, ie exactly "cover" each other (→ compare congruence illustration ). Congruent flat figures are therefore also called congruent . Figures that are not congruent are also called incongruent .

In the case of congruent plane polygons and spatial polyhedra , all corresponding line lengths and angle sizes must match.

In absolute geometry , two figures are called congruent if there is a movement of the point space through which one figure is mapped bijectively onto the other.

Comparison operator

A widely used symbol to express congruence is ≅, an equal sign with a tilde above it. It corresponds to the character for "roughly the same": Unicode U+2245 , HTML ≅ , in the typesetting system LaTeX -math mode \cong.

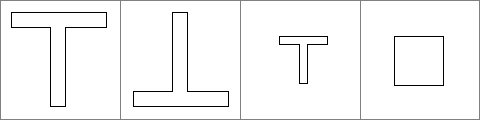
example

The first two figures are congruent. The third one has the same shape but is smaller. It is therefore similar to the first and second figures, but not congruent. The last figure does not have the same shape and is therefore neither similar nor congruent to the T-shaped figures.

Congruence of triangles

It is particularly easy to check the congruence of triangles using the following five congruence theorems , which provide simple criteria under which two triangles are congruent:

Two flat triangles agree in

sss: three side lengths or
sws: two side lengths and the dimension of the included angle or
Ssw: two side lengths and the dimension of the angle opposite the longer side or
wsw: a side length and the dimensions of the two adjacent angles or
wws: a side length, the dimension of an adjacent and that of the opposite angle

match, then they also match in the other side lengths or angular dimensions and are therefore congruent.

The maximum number of independent determinants (quantities that determine the congruence) is three for a flat triangle. Not only side length or angle can be determinants, but also the incircle radius , circumferential radius , height , length of a side bisector , area etc.

Congruence of n corners

For the congruent definition of a flat polygon , two additional determination pieces are required for each additional corner. Thus, the maximum number of independent determiners for the corner is . ${\ displaystyle n}$ ${\ displaystyle 2n-3}$

Congruence in spatial geometry

In stereometry (spatial geometry), polyhedra are also referred to as congruence of corners if two corners combine the same number of edges and surfaces with the same angles (in the same order); not only must the angles in the side surfaces of the polyhedron be the same, but also all angles between corresponding pairs of edges. If necessary, it must be possible to convert one corner into the other by means of a congruence mapping .

Comments

↑ Since the third is also given in the plane triangle because of the angle sum of 180 ° with two angles, wws is a direct consequence of wsw .

[1] Since the third is also given in the plane triangle because of the angle sum of 180 ° with two angles, wws is a direct consequence of wsw .