Normal form

The normal form , normal form or normal equation is in mathematics a special form of a linear equation or plane equation . In the normal form, a straight line in the Euclidean plane or a plane in Euclidean space is represented by a support vector and a normal vector . A straight line or plane then consists of those points in the plane or in space for which the difference vector from the position vector and support vector is perpendicular to the normal vector. The normal form is thus a special implicit representation of the straight line or plane.

A variant of the normal form is the Hessian normal form, in which the normal vector is normalized and oriented and the distance from the coordinate origin is used instead of the support vector .

Normal form of a straight line equation

Normal form of the straight line equation ${\displaystyle x+2y-6=0}$

presentation

In the normal form, a straight line in the plane is described by a support vector and a normal vector . A straight line then consists of those points in the plane whose position vectors give the equation ${\displaystyle {\vec {p}}}$ ${\displaystyle {\vec {n}}}$ ${\displaystyle {\vec {x}}}$

${\displaystyle ({\vec {x}}-{\vec {p}})\cdot {\vec {n}}=0}$

fulfill. Here the scalar product of two vectors denotes , which is zero if the vectors are perpendicular to one another. The support vector is the position vector of any point on the straight line, which is also referred to as the support point or reference point. The normal vector is a vector that forms a right angle with the straight line . In the normal form, the points of the straight line are therefore implicitly defined in that the difference vector from the position vector and the support vector is perpendicular to the normal vector of the straight line. An equivalent representation of the normal form is ${\displaystyle \cdot }$

${\displaystyle {\vec {x}}\cdot {\vec {n}}={\vec {p}}\cdot {\vec {n}}}$.

A point whose position vector does not satisfy the normal equation lies for on that side of the straight line into which the normal vector points, and otherwise on the other side. ${\displaystyle {\vec {x}}}$ ${\displaystyle {\vec {x}}\cdot {\vec {n}}>{\vec {p}}\cdot {\vec {n}}}$

example

The normal form of a straight line equation is written out

${\displaystyle (x_{1}-p_{1})\cdot n_{1}+(x_{2}-p_{2})\cdot n_{2}=0}$.

In the picture above, for example, is the support vector and the normal vector , and one obtains as a straight line equation ${\displaystyle {\vec {p}}={\tbinom {2}{2}}}$ ${\displaystyle {\vec {n}}={\tbinom {1}{2}}}$

${\displaystyle (x_{1}-2)\cdot 1+(x_{2}-2)\cdot 2=0}$.

Each choice of which satisfies this equation, for example or , then corresponds to a straight line point. ${\displaystyle (x_{1},x_{2})}$ ${\displaystyle (2,2)}$ ${\displaystyle (4,1)}$

calculation

From the parametric form

A normal vector of the straight line can be determined from the parametric form of a straight line equation by interchanging the two components of the direction vector of the straight line and changing the sign of one of the two components, that is to say ${\displaystyle {\vec {u}}}$

${\displaystyle {\vec {n}}={\begin{pmatrix}-u_{2}\\u_{1}\end{pmatrix}}}$.

The support vector can be taken from the parametric form. ${\displaystyle {\vec {p}}}$

From the two-point form

From the two-point form of a straight line equation, a direction vector of the straight line is first determined as a difference vector between the position vectors and the two points and then proceeded as with the parameter form, that is ${\displaystyle {\vec {p}}}$ ${\displaystyle {\vec {q}}}$

${\displaystyle {\vec {n}}={\begin{pmatrix}-(q_{2}-p_{2})\\q_{1}-p_{1}\end{pmatrix}}}$.

The position vector of one of the points can be used as a support vector . ${\displaystyle {\vec {p}}}$

From the coordinate form

From the coordinate form of a straight line equation with the parameters and , a normal vector of the straight line can be directly used as ${\displaystyle a,b}$ ${\displaystyle c}$

${\displaystyle {\vec {n}}={\begin{pmatrix}a\\b\end{pmatrix}}}$

read off. A support vector for the straight line is obtained by choosing whether or not it is zero ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle {\vec {p}}={\begin{pmatrix}c/a\\0\end{pmatrix}}}$   or   . ${\displaystyle {\vec {p}}={\begin{pmatrix}0\\c/b\end{pmatrix}}}$

In this way, a normal vector and a support vector can also be determined from the axis intercept form of a straight line equation.

Normal form of a plane equation

Normal form of a plane equation

presentation

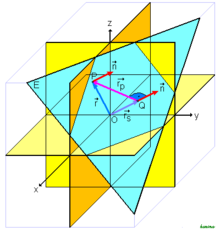
Analogously, a plane in three-dimensional space in the normal form is also described by a support vector and a normal vector . A plane then consists of those points in space whose position vectors give the equation ${\displaystyle {\vec {p}}}$ ${\displaystyle {\vec {n}}}$ ${\displaystyle {\vec {x}}}$

${\displaystyle ({\vec {x}}-{\vec {p}})\cdot {\vec {n}}=0}$

fulfill. The support vector is in turn the position vector of any point in the plane and the normal vector is a vector that is perpendicular to the plane. This means that the normal vector forms a right angle with all straight lines in the plane that run through the support point. An equivalent representation of the normal form is again

${\displaystyle {\vec {x}}\cdot {\vec {n}}={\vec {p}}\cdot {\vec {n}}}$

and a point whose position vector satisfies the normal equation lies on the plane. If so , then the point lies on that side of the plane into which the normal vector points, otherwise on the other side. ${\displaystyle {\vec {x}}}$ ${\displaystyle {\vec {x}}\cdot {\vec {n}}>{\vec {p}}\cdot {\vec {n}}}$

example

Written out is the normal form of a plane equation

${\displaystyle (x_{1}-p_{1})\cdot n_{1}+(x_{2}-p_{2})\cdot n_{2}+(x_{3}-p_{3})\cdot n_{3}=0}$.

For example, if the support vector and the normal vector are used , the plane equation is obtained ${\displaystyle {\vec {p}}=(3,2,1)^{T}}$ ${\displaystyle {\vec {n}}=(2,-1,2)^{T}}$

${\displaystyle (x_{1}-3)\cdot 2+(x_{2}-2)\cdot (-1)+(x_{3}-1)\cdot 2=0}$.

Each choice of that satisfies the plane equation, for example or , then corresponds to a plane point. ${\displaystyle (x_{1},x_{2},x_{3})}$ ${\displaystyle (2,0,1)}$ ${\displaystyle (1,2,3)}$

calculation

From the parametric form

From the parametric form of a plane equation with the two direction vectors and a normal vector of the plane can be obtained by calculating the cross product ${\displaystyle {\vec {u}}}$ ${\displaystyle {\vec {v}}}$

${\displaystyle {\vec {n}}={\vec {u}}\times {\vec {v}}}$

determine. The support vector can be taken from the parametric form. ${\displaystyle {\vec {p}}}$

From the three-point form

From the three points form a plane equation first two direction vectors of the difference vectors between the position vectors are , and each of two points is determined and then as the parameter form the cross product ${\displaystyle {\vec {p}}}$ ${\displaystyle {\vec {q}}}$ ${\displaystyle {\vec {r}}}$

${\displaystyle {\vec {n}}=({\vec {q}}-{\vec {p}})\times ({\vec {r}}-{\vec {p}})}$

calculated. The position vector of one of the points can be used as a support vector . ${\displaystyle {\vec {p}}}$

From the coordinate form

A normal vector of the plane can be derived from the coordinate form of a plane equation with the parameters and as ${\displaystyle a,b,c}$ ${\displaystyle d}$

${\displaystyle {\vec {n}}={\begin{pmatrix}a\\b\\c\end{pmatrix}}}$

read off. A support vector is obtained, depending on which of the numbers is not equal to zero, by choosing ${\displaystyle a,b,c}$

${\displaystyle {\vec {p}}={\begin{pmatrix}d/a\\0\\0\end{pmatrix}},~{\vec {p}}={\begin{pmatrix}0\\d/b\\0\end{pmatrix}}}$   or   . ${\displaystyle {\vec {p}}={\begin{pmatrix}0\\0\\d/c\end{pmatrix}}}$

Analogously, a normal vector and a support vector can also be determined in this way from the axis intercept form of a plane equation.

Derivation

To derive the normal form of a plane equation

The position vector of any straight line or plane point can be expressed as a sum ${\displaystyle {\vec {x}}}$

${\displaystyle {\vec {x}}={\vec {x}}_{s}+{\vec {x}}_{p}}$

represent, where perpendicular to the straight line or plane, i.e. parallel to , and parallel to the straight line or plane, i.e. perpendicular to . Then ${\displaystyle {\vec {x}}_{s}}$ ${\displaystyle {\vec {n}}}$ ${\displaystyle {\vec {x}}_{p}}$ ${\displaystyle {\vec {n}}}$

${\displaystyle {\vec {x}}\cdot {\vec {n}}=({\vec {x}}_{p}+{\vec {x}}_{s})\cdot {\vec {n}}={\vec {x}}_{p}\cdot {\vec {n}}+{\vec {x}}_{s}\cdot {\vec {n}}={\vec {x}}_{s}\cdot {\vec {n}}}$,

since the scalar product of mutually perpendicular vectors is always zero. The proportion is the same for every point on the straight line or plane, so it is constant for every point on the straight line or plane . This follows the normal form ${\displaystyle {\vec {x}}_{p}\cdot {\vec {n}}}$ ${\displaystyle {\vec {x}}_{s}}$ ${\displaystyle {\vec {x}}\cdot {\vec {n}}={\vec {x}}_{s}\cdot {\vec {n}}}$

${\displaystyle {\vec {x}}\cdot {\vec {n}}-{\vec {p}}\cdot {\vec {n}}=({\vec {x}}-{\vec {p}})\cdot {\vec {n}}=0}$,

where any selected point is on the straight line or plane. ${\displaystyle {\vec {p}}}$

generalization

In general, a normal equation describes a hyperplane in -dimensional Euclidean space. In -dimensional Euclidean space, a hyperplane consists of those points whose position vectors correspond to the equation ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle {\vec {x}}}$

${\displaystyle ({\vec {x}}-{\vec {p}})\cdot {\vec {n}}=0}$

respectively

${\displaystyle {\vec {x}}\cdot {\vec {n}}={\vec {p}}\cdot {\vec {n}}}$

fulfill. It is only calculated with -component instead of two- or three-component vectors. A hyperplane divides the -dimensional space into two parts called half-spaces . If so , then the point lies in that half-space into which the normal vector points, otherwise in the other. A point whose position vector satisfies the normal equation lies exactly on the hyperplane. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle {\vec {x}}\cdot {\vec {n}}>{\vec {p}}\cdot {\vec {n}}}$

literature

• Lothar Papula: Mathematical formula collection: For engineers and natural scientists . Springer, 2009, ISBN 978-3-8348-9598-1 .
• Harald Scheid, Wolfgang Schwarz: Elements of linear algebra and analysis . Springer, 2009, ISBN 978-3-8274-2255-2 .

Web links

• Convert level from parametric form to normal form. In: Serlo. Retrieved February 23, 2014 . 
• Convert plane from coordinate form to normal form. In: Serlo. Retrieved February 23, 2014 .