Octahedron of horror

The octahedron of horror is a term popularized by the media for a mathematical task in the field of linear algebra and analytical geometry that was asked in the central high school in North Rhine-Westphalia in 2008. Since it was felt by many students as too difficult and, together with the Nowitzki problem ( stochastics ), was held responsible for the poor performance of many students in the field of mathematics, it found a greater resonance in the media and developed into one over time Symbol for the problems of the newly introduced Central Abitur in North Rhine-Westphalia.

Background and reception

After comparatively few problems had arisen with the new Central Abitur, which was introduced the previous year, major problems arose in 2008, particularly in the area of ​​mathematics, which led to protests by students and teachers and attracted national attention. The math problems that caused unexpected great difficulties for many students were the octahedron problem and a probability calculus problem for throws by basketball player Dirk Nowitzki , which has since been referred to as the Nowitzki problem .

The octahedron task was initially referred to by students in internal discussions as the octahedron of horror . This designation was then quickly adopted by the media and was also found in various headlines in press publications. For example, the Süddeutsche Zeitung titled its report on the Abitur in North Rhine-Westphalia with "Octahedron of horror" . This term was later adopted by the specialist literature and is often cited as an example of problems with the central high school diploma in North Rhine-Westphalia.

Initial feedback on the difficulties was made known via spickmich , an Internet portal for schoolchildren. In a (non-representative) survey conducted by the portal among 1000 students who had worked on the controversial math problems, 50% stated that they had to take re-examinations or discrepancies. Protests were also organized on another Internet platform, the Maths Boycott initiative collected 2,778 signatures from parents, teachers and students for the demand that the math grades be increased across the board. Criticism also came from the Philologists Association of North Rhine-Westphalia, and several mathematics professors particularly criticized the formulation of the Nowitzki problem. Large parts of the press were also critical of the tasks, process and crisis management of the Abitur by the government of North Rhine-Westphalia, there was talk of an "Abi chaos" and "math chaos".

Due to increasing public pressure, the Minister of Education, Barbara Sommer ( CDU ), instead of the usual reviews for individual cases, finally set a general repeat date for June 17, which was open to all students who had completed the octahedron or Nowitzki task. In addition, she set up a new commission based at the University of Dortmund under the direction of Wilfried Bos , whose task it is to assess future Abitur assignments.

Grade statistics

Around 34,000 students took a written math exam, and around 20,000 of them (60%) completed the octahedron problem. The Nowitzki task, on the other hand, was only worked on by around 900 students and thus played a rather subordinate role in the difficulties. In addition, a sample carried out by the ministry, unlike the octahedron task, did not reveal any evidence that the Nowitzki task caused particular problems for the students. At grammar schools, an average grade of 8.2 points ( possible grade points: 0 to 15 ) was achieved in exams , which exactly corresponded to the average previous grade. At comprehensive schools, however, only an average grade of 4.6 points was achieved, which was also 2.3 points below the average previous grade of 6.9 points. In the advanced courses, 11.7% of the pupils at grammar schools and 40.2% at comprehensive schools had a negative deviation of three or more grade points compared to the previous grade. The number of students who achieved an underperformance (less than 5 points) in the advanced course exam was 16.8% in grammar schools and 54.5% in comprehensive schools, an increase of 5% for grammar schools and 10.6% for Comprehensive schools over the previous year meant. 1801 students took part in the offered repeat exam on June 17; The advanced course students improved their exam grade by an average of 1.8 points and the basic course students by 2.7 points.

Didactic point of view

The senior government school director Norbert Stirba commented on the octahedron task in an interview in autumn 2008. According to him, a difference to the Abitur of the previous year was that this time, even more high-performing students had difficulties with the task. This was partly because it was presumably too time-consuming and partly because it placed an emphasis on geometrical intuition, whereas many students' lessons had focused on analytical calculation methods.

The mathematician Hans Niels Jahnke described the octahedron problem as mathematically attractive, but pointed out that its solution required creativity and a lot of arithmetic.

The evaluation of the octahedron task by experts was overall less critical than for the Nowitzki task. While the latter was rated by math professors as "unsolvable" and "nonsensical" without additional assumptions by the student and criticized for the lack of an explicit reference to these, the former was viewed both as solvable and as appropriate in terms of the degree of difficulty of the individual subtasks. However, it was seen as too extensive for the time available and also criticized from the point of view of mathematics didactics. For example, the mathematics didactician Kaenders argues that a mathematical competence is characterized precisely by choosing the simplest possible representation for a mathematical modeling. Accordingly, for investigations on an octahedron one would place it in a coordinate system in such a way that its center point lies at the origin of the coordinate system and a simpler representation would also be chosen for cutting planes. The representation chosen for the octahedron task is therefore mathematically nonsensical, not authentic and presumably only served to artificially increase the (technical) difficulty of the task.

Task

illustration 1

Figure 2

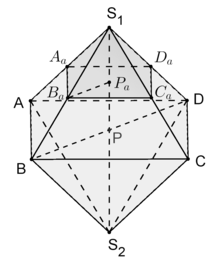
Both the basic and advanced course exercises begin with the same definition of an octahedron given below and the two figures on the right. In addition, the same aids were permitted for both, namely a scientific pocket calculator ( WTR or GTR ), a collection of mathematical formulas and a dictionary of German spelling.

An octahedron is a regular polyhedron whose surface consists of eight congruent equilateral triangles . Each octahedron can be inscribed on a cube in such a way that the corner points of the octahedron lie in the center of the side faces of the cube.

intensified course

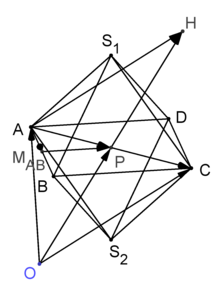
The corner points and of the octahedron shown in Figure 1 are given. This octahedron is inscribed in the above-mentioned way in the illustrated cube with the corners to . ${\displaystyle ABCDS_{1}S_{2}}$ ${\displaystyle A(13|-5|3),B(11|3|1),C(5|3|7)}$ ${\displaystyle S_{1}(13|1|9)}$ ${\displaystyle P_{1}}$ ${\displaystyle P_{8}}$

a)

The distance between two parallel sides of an octahedron is called the "thickness of the octahedron" . Calculate the thickness of the octahedron shown as the distance of the point from the plane . (8 points) ${\displaystyle C}$ ${\displaystyle ABS_{1}}$

b)

Determine the coordinates of the corner points and the depicted cube. (8 points) ${\displaystyle P_{6}}$ ${\displaystyle P_{8}}$

c)

The center of the track is , the midpoint of the segment is ; be the straight line that passes through these points and . The octahedron is rotated around the straight line as the axis of rotation so that the point moves into the new position . Show that the corresponding angle of rotation is. Determine the coordinates of the point as the new position of the corner point after the rotation. (11 points) ${\displaystyle AB}$ ${\displaystyle M_{AB}}$ ${\displaystyle CD}$ ${\displaystyle M_{CD}}$ ${\displaystyle g}$ ${\displaystyle M_{AB}}$ ${\displaystyle M_{CD}}$ ${\displaystyle g}$ ${\displaystyle A(13|-5|3)}$ ${\displaystyle A'(12+2\cdot {\sqrt {2}}|-1+{\sqrt {2}}|2+2\cdot {\sqrt {2}})}$ ${\displaystyle \alpha =90^{\circ }}$ ${\displaystyle B'}$ ${\displaystyle B}$

d)

Through be given a host of levels ; be the straight line that passes through the points and . Show that each plane of the family is orthogonal to the straight line. Determine the intersection of the plane with the straight line . [For control: ] For the plane cuts a pyramid with the tip of the octahedron shown (see Figure 2). Find the volume of the truncated pyramid. (15 points) ${\displaystyle E_{a}:2x_{1}+x_{2}+2x_{3}+9(2a-5)=0,\,a\in \mathbb {R} }$ ${\displaystyle E_{a}}$ ${\displaystyle h}$ ${\displaystyle S_{1}}$ ${\displaystyle S_{2}(5|-3|1)}$ ${\displaystyle E_{a}}$ ${\displaystyle h}$ ${\displaystyle P_{a}}$ ${\displaystyle E_{a}}$ ${\displaystyle h}$ ${\displaystyle P_{a}(13-4a|1-2a|9-4a)}$ ${\displaystyle 0<a\leq 1}$ ${\displaystyle E_{a}}$ ${\displaystyle S_{1}}$ ${\displaystyle V_{a}}$

e)

Six pyramids with the same volume V are cut from the octahedron in such a way that each corner of the octahedron is the tip of a pyramid and the base of each cut pyramid is parallel to the opposite side of the cube (cf. exercise part d)). A residual body is created . Describe the properties of this residual body for and with regard to the number and properties of its side faces. (8 points) ${\displaystyle R_{a}\,(0<a\leq {\tfrac {1}{2}})}$ ${\displaystyle R_{a}}$ ${\displaystyle a={\tfrac {1}{3}}}$ ${\displaystyle a={\tfrac {1}{2}}}$

Basic course

The points and are given . ${\displaystyle A(13|-5|3),B(11|3|1),C(5|3|7)}$ ${\displaystyle S_{1}(13|1|9)}$

a)

Justify: The points and are the corner points of a right-angled and isosceles triangle. Calculate the coordinates of the point so that the points and form a square. (8 points) ${\displaystyle A(13|-5|3),B(11|3|1)}$ ${\displaystyle C(5|3|7)}$ ${\displaystyle D}$ ${\displaystyle A,B,C}$ ${\displaystyle D}$

b)

The plane contains the square . Find an equation of the plane in parametric and coordinate form. [To check: ] (11 points) ${\displaystyle E}$ ${\displaystyle ABCD}$ ${\displaystyle E}$ ${\displaystyle E:\,2x_{1}+x_{2}+2x_{3}-27=0}$

c)

The point that is not in the plane is mirrored on the plane so that the mirror point that is too symmetrical is created. Determine the coordinates of the point . Justify: The body with the corner points and is an octahedron (7 points) ${\displaystyle S_{1}(13|1|9)}$ ${\displaystyle E}$ ${\displaystyle E}$ ${\displaystyle S_{1}}$ ${\displaystyle S_{2}}$ ${\displaystyle S_{2}}$ ${\displaystyle A,B,C,D,S_{1}}$ ${\displaystyle S_{2}}$

d)

According to Figure 1, the octahedron is inscribed on a cube in such a way that the corner points of the octahedron lie in the center of the side faces of this cube. Determine the coordinates of the corner points and the cube (10 points) ${\displaystyle ABCDS_{1}S_{2}}$ ${\displaystyle P_{6}}$ ${\displaystyle P_{8}}$

e)

A pyramid-shaped piece is cut from the octahedron so that the tip of the pyramid is the point and the edges of the cut pyramid are the same length (see Figure 2). Find the volume of the truncated pyramid in the event that its edge length is a third of the length of the octahedron edge . Now pyramids of the same size are cut off with the edge length from all other corners of the octahedron , so that a residual body is created. Describe this residual body for the case in terms of the number and properties of its side surfaces (number of corners, side lengths). Describe the rest of the body for the case in terms of the number and properties of its side faces. (14 points) ${\displaystyle ABCDS_{1}S_{2}}$ ${\displaystyle S_{1}}$ ${\displaystyle S_{1}}$ ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle AS_{1}}$ ${\displaystyle ABCDS_{1}S_{2}}$ ${\displaystyle k}$ ${\displaystyle R_{k}}$ ${\displaystyle R_{k}}$ ${\displaystyle k={\tfrac {1}{3}}|AS_{1}|}$ ${\displaystyle R_{k}}$ ${\displaystyle k={\tfrac {1}{2}}|AS_{1}|}$

solution

In the following denote the position vectors , the vector connecting , the link and the length of the link or the distance between two points . ${\displaystyle {\vec {X}},{\vec {Y}}}$ ${\displaystyle {\overrightarrow {XY}}}$ ${\displaystyle XY}$ ${\displaystyle |XY|}$ ${\displaystyle X,Y}$

intensified course

a)

Octahedron with thickness ${\displaystyle |CM|}$

Cross section with thickness ${\displaystyle h_{R}}$
${\displaystyle r^{2}=\left({\tfrac {d_{1}}{2}}\right)^{2}+\left({\tfrac {d_{2}}{2}}\right)^{2}}$
${\displaystyle \arccos(\alpha )={\frac {2r^{2}-d_{1}^{2}}{2r^{2}}}}$
${\displaystyle h_{R}=\sin(\alpha )\cdot r}$
${\displaystyle F_{R}={\frac {d_{1}\cdot d_{2}}{2}}}$
${\displaystyle s={\frac {r+r+d_{1}}{2}}}$
${\displaystyle F_{R}=2{\sqrt {s(s-r)^{2}(s-d_{1})}}}$
${\displaystyle h_{R}={\frac {F_{R}}{r}}}$

The triangle lies in the following plane in parametric form: ${\displaystyle ABS_{1}}$

${\displaystyle E_{ABS_{1}}:\,{\vec {S_{1}}}+r\cdot {\overrightarrow {S_{1}A}}+s\cdot {\overrightarrow {S_{1}B}}}$

The vectors spanning the plane and the position vector of the point can be inserted into the formula for the distance between a point and a plane , resulting in: ${\displaystyle C}$

${\displaystyle {\begin{aligned}{\overrightarrow {S_{1}A}}&={\vec {A}}-{\vec {S_{1}}}={\begin{pmatrix}0\\-6\\-6\end{pmatrix}}\\{\overrightarrow {S_{1}B}}&={\vec {B}}-{\vec {S_{1}}}={\begin{pmatrix}-2\\2\\8\end{pmatrix}}\\\end{aligned}}}$

${\displaystyle d(C,E_{ABS_{1}})={\frac {|({\vec {C}}-{\vec {S_{1}}})\cdot ({\overrightarrow {S_{1}A}}\times {\overrightarrow {S_{1}B}})|}{|{\overrightarrow {S_{1}A}}\times {\overrightarrow {S_{1}B}}|}}=4{\sqrt {3}}}$

Alternatively, you can also calculate the point of intersection of the plane with the straight line running through it, which has a normal vector of the plane (e.g. ) as a direction vector , and then use the distance formula for points on and the point of intersection. ${\displaystyle C}$ ${\displaystyle {\vec {S_{1}A}}\times {\vec {S_{1}B}}}$ ${\displaystyle C}$

Another possibility is to exploit the symmetry of the octahedron, because of the intersection of the medians of the equilateral triangles and are connected by a distance that is perpendicular to their surfaces, and thus corresponds to the thickness. One uses still, the medians that in the ratio 2: 1 cut, it can be the points of intersection and with the aid of the center points and of the sides and calculated as follows: ${\displaystyle ABS_{1}}$ ${\displaystyle CD_{2}}$ ${\displaystyle L}$ ${\displaystyle N}$ ${\displaystyle M_{AB}}$ ${\displaystyle M_{CD}}$ ${\displaystyle AB}$ ${\displaystyle CD}$

${\displaystyle {\vec {N}}={\vec {S_{1}}}+{\frac {2}{3}}({\overrightarrow {M_{AB}}}-{\vec {S_{1}}})={\frac {1}{3}}{\begin{pmatrix}37\\-16\\13\end{pmatrix}}}$

${\displaystyle {\vec {L}}={\vec {S_{2}}}+{\frac {2}{3}}({\overrightarrow {M_{CD}}}-{\vec {S_{2}}})={\frac {1}{3}}{\begin{pmatrix}17\\-5\\17\end{pmatrix}}}$

The thickness is now obtained by calculating the distance between the two points and : ${\displaystyle L}$ ${\displaystyle N}$

${\displaystyle d=|{\vec {L}}-{\vec {N}}|={\sqrt {(L_{x}-N_{x})^{2}+(L_{y}-N_{y})^{2}+(L_{z}-N_{z})^{2}}}=4{\sqrt {3}}}$

An elementary geometric derivation is also possible, which only uses the edge lengths of the octahedron. If you look at the plane that runs through and through the middle of the sides , you get a diamond with the corner points . The thickness of the octahedron then corresponds to the height in this diamond. From the diamond you now know its side length and its diagonals and you can calculate this from the given corner points of the octahedron. The height can now be obtained by first calculating an interior angle with the help of the cosine law and with this the height. If you first determine the area of ​​the diamond based on its diagonals and / or Heron's formula , you can also determine the height without trigonometry by dividing the area by the length of the side . ${\displaystyle S_{1},S_{2}}$ ${\displaystyle M_{AB},M_{CD}}$ ${\displaystyle AB,CD}$ ${\displaystyle S_{1},S_{2},M_{AB},M_{CD}}$ ${\displaystyle r=|S_{1}M_{AB}|}$ ${\displaystyle d_{1}=|M_{AB}M_{CD}|=|BC|}$ ${\displaystyle d_{2}=|S_{1}S_{1}|}$ ${\displaystyle d_{1}}$ ${\displaystyle d_{2}}$ ${\displaystyle r}$

b)

Calculation of and ${\displaystyle P_{6}}$ ${\displaystyle P_{8}}$

In order to calculate and from the given points or the position vectors of the octahedron, one seeks how these can be put together from the given position vectors. One possibility is as follows: ${\displaystyle P_{6}}$ ${\displaystyle P_{8}}$

${\displaystyle {\begin{aligned}{\vec {P_{6}}}&={\vec {S_{1}}}+{\overrightarrow {AB}}={\vec {S_{1}}}+({\vec {B}}-{\vec {A}})={\begin{pmatrix}11\\9\\7\end{pmatrix}}\\{\vec {P_{8}}}&={\vec {S_{1}}}+{\overrightarrow {BA}}={\vec {S_{1}}}+({\vec {A}}-{\vec {B}})={\begin{pmatrix}15\\-7\\11\end{pmatrix}}\end{aligned}}}$

c)

First you need the point on the line of rotation that lies in the plane of rotation, this is the center point of the line . The angle between the vectors and is the angle of rotation. Since one only wants to prove one or orthogonality, it suffices to show that the scalar product of the two vectors is 0. ${\displaystyle M_{AB}}$ ${\displaystyle AB}$ ${\displaystyle {\overrightarrow {M_{AB}A}}}$ ${\displaystyle {\overrightarrow {M_{AB}A'}}}$ ${\displaystyle 90^{\circ }}$

${\displaystyle {\overrightarrow {M_{AB}}}={\frac {1}{2}}({\vec {A}}+{\vec {B}})={\begin{pmatrix}12\\-1\\2\end{pmatrix}}}$

${\displaystyle {\begin{aligned}{\overrightarrow {M_{AB}A}}&={\overrightarrow {A}}-{\overrightarrow {M_{AB}}}={\begin{pmatrix}1\\-4\\1\end{pmatrix}}\\{\overrightarrow {M_{AB}A'}}&={\overrightarrow {A'}}-{\overrightarrow {M_{AB}}}={\begin{pmatrix}2{\sqrt {2}}\\{\sqrt {2}}\\2{\sqrt {2}}\end{pmatrix}}\end{aligned}}}$

${\displaystyle {\overrightarrow {M_{AB}A}}\cdot {\overrightarrow {M_{AB}A'}}=1\cdot 2{\sqrt {2}}-4\cdot {\sqrt {2}}+1\cdot 2{\sqrt {2}}=0}$

Since a rotation leaves the relative position of and to each other unchanged, lie and lie on a common straight line (see drawing), so it can be calculated as follows: ${\displaystyle A}$ ${\displaystyle AB}$ ${\displaystyle A'}$ ${\displaystyle B'}$ ${\displaystyle B'}$

${\displaystyle {\overrightarrow {B'}}={\overrightarrow {M_{AB}}}-{\overrightarrow {M_{AB}A'}}={\begin{pmatrix}12-2{\sqrt {2}}\\-1-{\sqrt {2}}\\2-2{\sqrt {2}}\end{pmatrix}}}$

d)

Its normal vector can be read from the plane equation . In order to prove that the straight line is perpendicular to all planes , one has to show that its direction vector is a multiple of the normal vector or is linearly dependent on it. If you choose the direction vector as the direction vector of the straight line , you immediately see: ${\displaystyle E_{a}:2x_{1}+x_{2}+2x_{3}+9(2a-5)=0}$ ${\displaystyle {\vec {n}}}$ ${\displaystyle h}$ ${\displaystyle E_{a}}$ ${\displaystyle {\vec {n}}}$ ${\displaystyle {\overrightarrow {S_{2}S_{1}}}}$ ${\displaystyle h}$

${\displaystyle {\overrightarrow {S_{2}S_{1}}}={\vec {S_{1}}}-{\vec {S_{2}}}={\begin{pmatrix}13\\1\\9\end{pmatrix}}-{\begin{pmatrix}5\\-3\\1\end{pmatrix}}={\begin{pmatrix}8\\4\\8\end{pmatrix}}=4\cdot {\begin{pmatrix}2\\1\\2\end{pmatrix}}=4\cdot {\vec {n}}}$

Alternatively, the linear dependence of two vectors can also be demonstrated by showing that their cross product gives the zero vector:

${\displaystyle {\overrightarrow {S_{2}S_{1}}}\times {\vec {n}}={\begin{pmatrix}8\\4\\8\end{pmatrix}}\times {\begin{pmatrix}2\\1\\2\end{pmatrix}}={\begin{pmatrix}4\cdot 2-8\cdot 1\\8\cdot 2-8\cdot 2\\8\cdot 1-4\cdot 2\end{pmatrix}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}}$

With the direction vector selected above one has the following vector representation of the straight line : ${\displaystyle h}$

${\displaystyle h:{\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}={\vec {S1}}+t\cdot {\overrightarrow {S_{2}S_{1}}}={\begin{pmatrix}13\\1\\9\end{pmatrix}}+t\cdot {\begin{pmatrix}8\\4\\8\end{pmatrix}}={\begin{pmatrix}13+t\cdot 9\\1+t_{a}\cdot 4\\9+t_{a}\cdot 8\end{pmatrix}}}$

In order to calculate the point of intersection of the straight line with the plane, insert the coordinates obtained from the straight line representation into the plane equation and thus obtain a linear equation for , from which one can determine depending on : ${\displaystyle t}$ ${\displaystyle t}$ ${\displaystyle a}$

${\displaystyle 2\cdot (13+t_{a}\cdot 9)+(1+t_{a}\cdot 4)+2\cdot (9+t_{a}\cdot 8)+9(2a-5)=0\,\Rightarrow \,t_{a}=-{\frac {1}{2}}a}$

The parameter found in this way is now inserted into the straight line equation and thus the position vector of the intersection point sought is obtained ${\displaystyle t_{a}}$ ${\displaystyle P_{a}}$

${\displaystyle {\vec {P_{a}}}=h(t_{a})={\begin{pmatrix}13\\1\\9\end{pmatrix}}+\left(-{\frac {1}{2}}a\right)\cdot {\begin{pmatrix}8\\4\\8\end{pmatrix}}={\begin{pmatrix}13-4a\\1-2a\\9-4a\end{pmatrix}}}$

If you look at the calculation of the point, you can see that the connection vector is scaled by the factor : ${\displaystyle a}$ ${\displaystyle {\overrightarrow {S_{1}G}}}$ ${\displaystyle a}$

${\displaystyle \left(-{\frac {1}{2}}a\right)\cdot {\begin{pmatrix}8\\4\\8\end{pmatrix}}=a\cdot {\begin{pmatrix}-4\\-2\\-4\end{pmatrix}}=a\cdot {\overrightarrow {S_{1}G}}}$

The truncated pyramid is thus a scaled or centrically stretched version of the pyramid . So you only have to factor their volume with the factor to get the volume of the truncated pyramid. ${\displaystyle a}$ ${\displaystyle S_{1}ABCD}$ ${\displaystyle V}$ ${\displaystyle a^{3}}$ ${\displaystyle V_{a}}$

The following applies:

${\displaystyle {\begin{aligned}|{\overrightarrow {S_{1}G}}|&={\sqrt {(-4)^{2}+(-1)^{2}+(-4)^{2}}}=6\\|{\overrightarrow {AB}}|&={\sqrt {(11-13)^{2}+(3-(-5))^{2}+(1-34)^{2}}}=6{\sqrt {2}}\end{aligned}}}$

Together with the general formula for the volume of pyramids, the result for the volume of the truncated pyramid is: ${\displaystyle V={\tfrac {1}{3}}h\cdot G}$ ${\displaystyle V_{a}}$

${\displaystyle V_{a}=a^{3}V=a^{3}{\frac {1}{3}}|S_{1}G||AB|^{2}=144a^{3}}$

If one does not want to fall back on centric extensions (in space) and their properties, one can instead use the aspect ratios in the pyramid resulting from the ray theorems (see basic course exercise e)).

e)

If you cut off relatively small pyramids at the corners of the octahedron, you get a polyhedron whose surface consists of six squares and eight hexagons. The hexagons are created from triangles of the octahedron, each with three additional sides. If you enlarge the pyramids further and further, the three sides of the hexagons lying on the octahedron edges shrink further and further until they have disappeared and the intersecting edges of the pyramids meet directly. In this case a polyhedron is created, which consists of 6 squares and 8 equilateral triangles. The question now is for which case this occurs. Since the truncated pyramid is the pyramid stretched by the factor , the case we are looking for occurs and we get for the polyhedron with squares and hexagons. ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle S_{1}ABCD}$ ${\displaystyle a={\tfrac {1}{2}}}$ ${\displaystyle {\tfrac {1}{3}}<{\tfrac {1}{2}}}$ ${\displaystyle a={\tfrac {1}{3}}}$

• 

  ${\displaystyle a={\tfrac {1}{3}}}$

• 

  ${\displaystyle a={\tfrac {1}{2}}}$

Basic course

a)

A right angle in can be demonstrated by showing that the scalar product of the associated connection vectors is zero, that is, it holds. The isosceles of the triangle is demonstrated by calculating the length of the connection vectors and . The following applies: ${\displaystyle B}$ ${\displaystyle {\overrightarrow {BA}}\cdot {\overrightarrow {BC}}=0}$ ${\displaystyle ABC}$ ${\displaystyle |{\overrightarrow {BA}}|}$ ${\displaystyle |{\overrightarrow {BC}}|}$

${\displaystyle {\overrightarrow {BA}}={\vec {A}}-{\vec {B}}={\begin{pmatrix}13\\-5\\3\end{pmatrix}}-{\begin{pmatrix}11\\3\\1\end{pmatrix}}={\begin{pmatrix}2\\-8\\2\end{pmatrix}}}$

${\displaystyle {\overrightarrow {BC}}={\vec {C}}-{\vec {B}}={\begin{pmatrix}5\\3\\7\end{pmatrix}}-{\begin{pmatrix}11\\3\\1\end{pmatrix}}={\begin{pmatrix}-6\\0\\6\end{pmatrix}}}$

${\displaystyle {\overrightarrow {BA}}\cdot {\overrightarrow {BC}}=2\cdot (-6)+(-8)\cdot 0+2\cdot 6=0}$

${\displaystyle |{\overrightarrow {BA}}|={\sqrt {2^{2}+(-8)^{2}+2^{2}}}={\sqrt {72}}=6{\sqrt {2}}}$

${\displaystyle |{\overrightarrow {BC}}|={\sqrt {(-6)^{2}+0^{2}+6^{2}}}={\sqrt {72}}=6{\sqrt {2}}}$

The right angle in can also be shown by applying the reverse of the Pythagorean theorem , that is, showing that it holds. ${\displaystyle B}$ ${\displaystyle |{\overrightarrow {AC}}|^{2}=|{\overrightarrow {BA}}|^{2}+|{\overrightarrow {BC}}|^{2}}$

${\displaystyle {\vec {D}}={\vec {A}}+{\overrightarrow {BC}}={\begin{pmatrix}13\\-5\\3\end{pmatrix}}+\left[{\begin{pmatrix}5\\3\\7\end{pmatrix}}-{\begin{pmatrix}11\\3\\1\end{pmatrix}}\right]={\begin{pmatrix}7\\-5\\9\end{pmatrix}}}$

b)

The representation of the plane in parametric form is:

${\displaystyle E:{\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}={\vec {B}}+r\cdot {\overrightarrow {BA}}+s\cdot {\overrightarrow {BC}}={\begin{pmatrix}11\\3\\1\end{pmatrix}}+r\cdot {\begin{pmatrix}2\\-8\\2\end{pmatrix}}+s\cdot {\begin{pmatrix}-6\\0\\6\end{pmatrix}}}$

The coordinate form is obtained from the parametric form by multiplying it with a normal vector. A normal vector is obtained, for example, from the cross product of the two vectors and . ${\displaystyle {\overrightarrow {BA}}}$ ${\displaystyle {\overrightarrow {BC}}}$

${\displaystyle {\overrightarrow {BA}}\times {\overrightarrow {BC}}={\begin{pmatrix}2\\-8\\2\end{pmatrix}}\times {\begin{pmatrix}-6\\0\\6\end{pmatrix}}={\begin{pmatrix}(-8)\cdot 6-2\cdot 0\\2\cdot (-6)-2\cdot 6\\2\cdot 0-(-8)\cdot (-6)\end{pmatrix}}={\begin{pmatrix}-48\\-24\\-48\end{pmatrix}}=(-24)\cdot {\begin{pmatrix}2\\1\\2\end{pmatrix}}}$

If necessary, it makes sense not to use the result of the cross product directly as the normal vector, but rather a multiple of it, which offers a simpler representation. The following choice is available here:

${\displaystyle {\vec {n}}={\begin{pmatrix}2\\1\\2\end{pmatrix}}}$

If you multiply the parameter form of the plane with , you get: ${\displaystyle {\vec {n}}}$

${\displaystyle {\begin{aligned}&\,{\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}\times {\begin{pmatrix}2\\1\\2\end{pmatrix}}=\left[{\begin{pmatrix}11\\3\\1\end{pmatrix}}+r\cdot {\begin{pmatrix}2\\-8\\2\end{pmatrix}}+s\cdot {\begin{pmatrix}-6\\0\\6\end{pmatrix}}\right]\times {\begin{pmatrix}2\\1\\2\end{pmatrix}}\\\Rightarrow &\quad 2x_{1}+x_{2}+2x_{3}=(11\cdot 2+3\cdot 1+1\cdot 2)+0+0\\\Rightarrow &\quad 2x_{1}+x_{2}+2x_{3}-27=0\end{aligned}}}$

c)

Reflection of ${\displaystyle S_{1}}$

To get to the point on the plane you first need the straight line that runs through and is perpendicular to. With the normal vector calculated in b) as the direction vector , the representation has: ${\displaystyle S_{1}}$ ${\displaystyle E}$ ${\displaystyle h}$ ${\displaystyle S_{1}}$ ${\displaystyle E}$ ${\displaystyle {\vec {n}}}$ ${\displaystyle h}$

${\displaystyle h:{\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}={\begin{pmatrix}13\\1\\9\end{pmatrix}}+t\cdot {\begin{pmatrix}2\\1\\2\end{pmatrix}}={\begin{pmatrix}13+t\cdot 2\\1+t\\9+t\cdot 2\end{pmatrix}}}$

If you insert the coordinates of the straight lines in the coordinate form of the plane, you get an equation for the straight line parameter : ${\displaystyle t}$

${\displaystyle 2\cdot (13+2t)+(1+t)+2\cdot (9+2t)-27=0\,\Rightarrow \,t=-2}$

If you insert the value obtained for in the parametric representation of the straight line, you get the point . This is the intersection of the straight line and plane and also the point at which it is mirrored (understood as point mirroring). ${\displaystyle t}$ ${\displaystyle P}$ ${\displaystyle S_{1}}$

${\displaystyle {\vec {P}}=h(-2)={\begin{pmatrix}13\\1\\9\end{pmatrix}}+(-2)\cdot {\begin{pmatrix}2\\1\\2\end{pmatrix}}={\begin{pmatrix}9\\-1\\5\end{pmatrix}}}$

The mirror point is now obtained by adding to the connection vector or by doubling the parameter value in the straight line representation: ${\displaystyle S_{2}}$ ${\displaystyle {\vec {P}}}$ ${\displaystyle {\overrightarrow {S_{1}P}}}$

${\displaystyle {\vec {S_{2}}}=h(-4)={\begin{pmatrix}13\\1\\9\end{pmatrix}}+(-4)\cdot {\begin{pmatrix}2\\1\\2\end{pmatrix}}={\begin{pmatrix}5\\-3\\1\end{pmatrix}}}$

According to the definition of the octahedron given in the exercise, one has to show that the eight outer surfaces of are equilateral triangles. Since the figure is caused by a reflection, it is sufficient for the triangles , , and proven. From a) we know already that the length of , , and is so remains to be calculated: ${\displaystyle ABCDS_{1}S_{2}}$ ${\displaystyle ABS_{1}}$ ${\displaystyle BCS_{1}}$ ${\displaystyle CDS_{1}}$ ${\displaystyle ADS_{1}}$ ${\displaystyle AB}$ ${\displaystyle BC}$ ${\displaystyle CD}$ ${\displaystyle AD}$ ${\displaystyle 6{\sqrt {2}}}$

${\displaystyle |AS_{1}|={\sqrt {(13-13)^{2}+(-5-1)^{2}+(3-9)^{2}}}=6{\sqrt {2}}}$

${\displaystyle |BS_{1}|={\sqrt {(11-13)^{2}+(3-1)^{2}+(1-9)^{2}}}=6{\sqrt {2}}}$

${\displaystyle |CS_{1}|={\sqrt {(5-13)^{2}+(3-1)^{2}+(7-9)^{2}}}=6{\sqrt {2}}}$

${\displaystyle |DS_{1}|={\sqrt {(7-13)^{2}+(-5-1)^{2}+(9-9)^{2}}}=6{\sqrt {2}}}$

O is the origin of the coordinates
${\displaystyle {\vec {C}}={\overrightarrow {OC}}={\overrightarrow {AH}}}$
${\displaystyle {\overrightarrow {AM_{AB}}}={\tfrac {1}{2}}{\overrightarrow {AB}}}$
${\displaystyle {\overrightarrow {M_{AB}P}}={\tfrac {1}{2}}{\overrightarrow {BC}}}$
${\displaystyle {\vec {P}}={\overrightarrow {OP}}={\tfrac {1}{2}}{\overrightarrow {OH}}={\tfrac {1}{2}}\left({\vec {A}}+{\vec {C}}\right)}$

So it is an equilateral triangle and accordingly an octahedron. ${\displaystyle ABCDS_{1}S_{2}}$

Alternatively, you can show that the center is the square . This then makes a square pyramid with four edges of equal length. So you only have to calculate an edge length, for example , and compare it with the side length of the square . For the proof of the center point property of one can show, for example, that one of the following equations is satisfied: ${\displaystyle P}$ ${\displaystyle ABCD}$ ${\displaystyle ABCDS_{1}}$ ${\displaystyle |AS_{1}|}$ ${\displaystyle ABCD}$ ${\displaystyle P}$ ${\displaystyle P}$

${\displaystyle {\vec {P}}={\frac {1}{2}}({\vec {A}}+{\vec {C}})}$

${\displaystyle {\vec {P}}={\frac {1}{2}}({\vec {B}}+{\vec {D}})}$

${\displaystyle {\vec {P}}=A+{\frac {1}{2}}({\overrightarrow {AB}}+{\overrightarrow {BC}})}$

d)

The task and therefore the solution is identical to the advanced course task b) (see there)

e)

Ray theorem:
${\displaystyle {\frac {|A_{a}B_{a}|}{|AB|}}={\frac {|S_{1}A_{a}|}{|S_{1}A|}}={\frac {|S_{1}P_{a}|}{|S_{1}P|}}}$

The volume of a square pyramid can be calculated using the formula , where the height of the pyramid and the side of the base square denote. These two quantities can be calculated, for example, with the aid of the ray theorem, since the distance ratio on the edge is known. The following applies: ${\displaystyle V={\tfrac {1}{3}}h_{pyr}a_{pyr}^{2}}$ ${\displaystyle h_{pyr}}$ ${\displaystyle a_{pyr}}$ ${\displaystyle AS_{1}}$

${\displaystyle {\begin{aligned}{\frac {1}{3}}={\frac {a_{pyr}}{|AB|}}&\,\Rightarrow \,a_{pyr}={\frac {1}{3}}|AB|\\{\frac {1}{3}}={\frac {h_{pyr}}{|S_{1}P|}}&\,\Rightarrow \,h_{pyr}={\frac {1}{3}}|S_{1}P|\end{aligned}}}$

With (from a)) and (from b)) one finally obtains for the volume: ${\displaystyle |AB|=6{\sqrt {2}}}$ ${\displaystyle |S_{1}P|={\sqrt {(9-13)^{2}+((-1)-1)^{2}+(5-9)^{2}}}=6}$

${\displaystyle V={\frac {1}{3}}h_{pyr}a_{pyr}^{2}={\frac {1}{3}}\left({\frac {6}{3}}\right)\left({\frac {6{\sqrt {2}}}{3}}\right)^{2}={\frac {16}{3}}}$

The question about the resulting polyhedra corresponds to the advanced course exercise e), where corresponds to the case and the case (see there). ${\displaystyle k={\tfrac {1}{3}}|AS_{1}|}$ ${\displaystyle a={\tfrac {1}{3}}}$ ${\displaystyle k={\tfrac {1}{2}}|AS_{1}|}$ ${\displaystyle a={\tfrac {1}{2}}}$

literature

• Hans-Wolfgang Henn, Andreas Filler: Didactics of Analytical Geometry and Linear Algebra: Understanding Algebraically - Illustrating and Using Geometry . Springer, 2015, ISBN 9783662434352 , pp. 233-234
• Wolfgang Alvermann: The Octrahedron of Horror . The Derive Newsletter # 77, March 2010, ISSN 1990-7079, pp. 35-39
• Maximilian Selinka, Jörg Stark: Mathematics 2009 . Klett, 2008, ISBN 978-3129298657 (Abitur preparation, contains the Abitur tasks 2007 and 2008 including solutions)

Web links

Commons : Octahedron of Horror  - Collection of images, videos and audio files

• Task and solution
• Folder of all math problems for the NRW Abitur from 2007 to 2015 , pp. 205–214, 301–313
• State parliament debate in NRW on the mathematics high school diploma 2008
• Franz-Reinhold Diepenbrock: mishaps, near mishaps and only supposed mishaps at the Central Mathematics Abitur in North Rhine-Westphalia in 2008, 2010 and 2011
• Armin Himmelrath: Incomprehensible, unclear, unsolvable - the Abitur chaos of North Rhine-Westphalia . Spiegel Online, June 4, 2008
• Amory Burchard: Math chaos with consequences . Tagesspiegel, June 11, 2008
• Tanyev Schultz: "Octahedron of Horror" . Süddeutsche Zeitung, June 7, 2008

Individual evidence

1. ↑ Ute Sproesser, Silvia Wessolowski, Claudia Wörn: Data, chance and the rest of the world: Didactic perspectives on applied mathematics . Springer, 2015, ISBN 9783658046699 , p. 15
2. ↑ ^{a b c} Peter V. Brinkemper: Beautiful new mathematics and the octahedron of horror . Telepolis, June 22, 2008
3. ↑ Jens Stubbe, Volker Schulte: The "octahedron of horror" . Westfalenpost, June 5, 2008
4. ↑ Tanyev Schultz: "Octahedron of Horror" . Süddeutsche Zeitung, June 7, 2008
5. ↑ see e.g. B. Drossel / Strietholt, Henn / Filler or Stender
6. ↑ Kristian Frugelj: Scandal over high school graduation tasks? . Die Welt, June 7, 2008
7. ↑ "Task unsolvable, solution nonsensical" . Westfalenpost, June 22, 2008
8. ↑ Christoph Lumme: Abitur 2008: The cube of horror . Westdeutsche Zeitung, May 22, 2008
9. ↑ Markus Flohr, Jochen Leffers: "Octahedron of Horror" - Math victims in North Rhine-Westphalia get a second chance . Spiegel Online, June 9, 2008
10. ↑ Theo Schumacher: Abi breakdown series despite expensive experts - Ministry wants to review 'Abi-Tüv' . Westdeutsche Allgemeine Zeitung, June 26, 2011
11. ↑ Breakdown-free central high school diploma . Süddeutsche Zeitung, May 17, 2010 (online)
12. ^ Arno Heissmeyer: Central Abitur, a second chance . Focus, June 9, 2008
13. ↑ Evaluation of the central high school diploma 2008 at grammar schools and comprehensive schools in North Rhine-Westphalia (accessed March 26, 2019)
14. ↑ Central exams 2008 . Newsletter September 25, 2008 (Interview with the leading government school director Norbert Stirba)
15. ↑ Stephan Hermsen: The chaos theory as an encore . Neue Ruhr Zeitung, June 10, 2008
16. ↑ Franz-Reinhold Diepenbrock: Basketball task from the Central Abitur in North Rhine-Westphalia (accessed August 22, 2020)
17. ↑ Franz-Reinhold Diepenbrock: mishaps, near mishaps and only supposed mishaps at the central mathematics high school in North Rhine-Westphalia in 2008, 2010 and 2011 (accessed March 24, 2019)
18. ↑ Peter Stender: Teacher interventions in the supervision of modeling questions on the basis of heuristic strategies . In: Rita Borromeo Ferri (ed.), Werner Blum (ed.): Teacher skills for teaching mathematical modeling: Concepts and transfer . Springer, 2018, ISBN 9783658226169 , p. 122
19. ↑ Rainer Kaenders: enthusiasm for mathematics . Inaugural lecture at the University of Cologne, October 24, 2008, pp. 10–13
20. ↑ ^{a b c} M GK HT 6, Ministry for Schools and Further Education of the State of North Rhine-Westphalia (Abitur exam 2008, basic course) ( online copy, pdf, pp. 205-214 )
21. ↑ ^{a b c} M LK HT 6, Ministry for Schools and Further Education of the State of North Rhine-Westphalia (Abitur exam 2008, advanced course) ( online copy ; online copy, pdf, pp. 301-313 )