Roll-Nick-Yaw angle
| Roll-Nick-Yaw angle ( Euler angle ) | |
|---|---|
| Rotation axes : | Move: |
| ↙ Longitudinal axis (roll / roll axis) : | Roll , sway |
| ↖ transverse axis (pitch axis) : | Nod, stamp |
| ↓ vertical axis (yaw axis) : | Yaw (roll) |
Roll-pitch-yaw angles , English roll-pitch-yaw angles , are special Euler angles (attitude angle) that are used to describe the orientation of a vehicle in three-dimensional space . This type of direction measurement and determination by rotation rate sensors was introduced for navigation in air traffic and is now used not only for aircraft but also for space, land and water vehicles.
Details
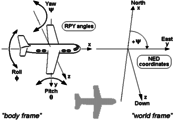
The angles taken over from the flight control describe three consecutive rotations that convert a fixed reference system ( world-frame ) into an object-related right - handed coordinate system ( body frame ). Its origin is thought to be in the center of the vehicle, whereby the angle designations are derived directly from the names of the three possible rotational movements of the vehicle around its body axes (see figure on the right). At the beginning of the rotations, the reference system and the body-fixed system match.
- Rollers (engl. Roll ) rotation about the longitudinally direction of the vehicle axis ( roll, roll or the longitudinal axis ). The term banking is also used for the bank angle .
- Nod (engl. Pitch , rarely nick ): rotation about the axis of the vehicle ( pitch or transverse axis ).
- Yaw (engl. Yaw ) rotation about the axis of the reference system ( yaw, vertical or vertical axis ). The terms heading or azimuth are sometimes used for the direction angle .
However, only the positive axis ( roll axis ) shows consistently, i.e. H. in space, air, water and land vehicles, to the front. For the positive and direction of the object system ( body frame ), on the other hand, there are two different conventions, depending on which external coordinate system ( world frame ) is used as the reference system:
- In the case of land vehicles that use the ENU (East-North-Up) system as the reference system, the positive y-axis ( pitch axis ) always points to the left or port side, and the positive - vertical to the xy plane of the vehicle - Axis ( yaw axis ) always upwards.
- In space, air and water vehicles including submarines, however, on grounds of compatibility with the traditional compass direction on the NED system (North-East-Down) to use as a reference system, the positive shows axis (Engl. Pitch axis always) in the direction of the right wing or to starboard and the positive axis ( yaw axis ) standing vertically on the plane of the vehicle always downwards.
What is "below" is defined somewhat differently for spacecraft such as space shuttles or satellites than for aircraft and ships: Depending on the objective of the flight, spacecraft use either a so-called coordinate system based on the current flight path instead of one of the two above-mentioned external coordinate systems. local reference system (engl. local frame ) or on the constellation ram and the vernal equinox (engl. vernal equinox ) and on the North-South axis of the Earth orienting absorbed. Inertial (. English inertial frame ):
Is it about the spacecraft, e.g. B. to keep a space shuttle in as constant a position as possible with regard to the sky when it orbits the earth, e.g. to carry out certain astronomical investigations, the inertial system is preferably used as the reference system , in which the RPY angle (0 | 0 | 0) is a position describe the space shuttle in which it orbits the earth with its wings parallel to the earth's equator, the bow pointing towards the vernal equinox and the belly pointing towards the polar star.
If, on the other hand, the aim is to keep the space shuttle in as constant a position as possible with respect to the earth's surface when it is orbiting the earth, for example to carry out certain earth-related investigations, the local reference system is preferably used instead as the reference system in which the RPY angle (0 | 0 | 0) describe a position of the space shuttle in which it orbits the earth like an airplane with the wings parallel to the earth's surface, the bow forward and the belly pointing to the center of the earth.
Even with three-axis stabilized satellites , such as the earth z. B. orbiting as communication satellites with a fixed orientation on the earth, the language just described has meanwhile become common for angles and axes of rotation. In this case, the positive axis of the satellite - as with the use of a local reference system by a space shuttle (see above) - points in the direction of its flight path around the earth, while the antennas of the satellite, which are aligned with the center of the earth, thus point in the direction of its positive z- Show the axis and finally its solar collectors rotate around the axis that is perpendicular to both axes (see fig.).
Since rotations of the satellite around its z-axis only have a minor influence on the orientation of its antennas in relation to the earth, the position control of the z-axis can work with a greater tolerance than that of the other two axes: Typical values for the yaw angle ( engl. yaw ) are ± 0.15 ° , English for the roll and pitch angles (. roll and pitch ), however, only ± 0.05 ° .
In robotics , roll-pitch-yaw angles are used to describe orientations (of the tool or other objects) in relation to a fixed base.
Finally, in aerodynamics, the term pitch is also used for the angle of attack of a propeller or rotor, in contrast to the above system , see Pitch (aerodynamics) .
"ZY′X" Convention "
The rotations always relate to the initially spatially fixed right-handed orthogonal base. The convention of the orientation of the angles follows the right-hand rule common in mathematics, a positive angle thus points counterclockwise. All other rotation axes result dynamically according to the defined sequence of rotations.
If one denotes the yaw angle, the pitch angle and the roll angle, the rotation matrix for this definition looks like this:
Is exactly the same , occur singularities, called gimbal lock on that manifest themselves in the fact that in these cases and are many solutions suddenly infinite. So z. B. for using the addition theorems the rotation matrix
and for the rotation matrix
Calculation from rotation matrix
Given a rotation matrix:
Then the angles can be calculated in the XYZ convention as follows (Craig, p. 47f):
In the case of the singularities mentioned above, however, the following formulas are useful:
Is , one expediently sets
If instead , it is expedient to set analogously
It is the " arc tangent with two arguments " that exists in many mathematical libraries and opposite the arc tangent function has the advantage of being the case distinctions for the four quadrants includes.
Other ways of describing the orientation are rotation matrix , quaternions or Euler's angles .
See also
literature
- John J. Craig: Introduction to Robotics . 2nd Edition. Addison-Wesley Publishing Company, Reading, Mass. [u. a.] 1989, ISBN 0-201-09528-9 .
Individual evidence
- ↑ NavCommand. Software for the configuration and operation of iMAR inertial measuring systems. Handling and user information. St. Ingbert 2005, pp. 11-12. http://www.imar-navigation.de/index.php/de/downloads/file/58-navcommand-manual.html ( page no longer available , search in web archives ) Info: The link was automatically marked as defective. Please check the link according to the instructions and then remove this notice.
- ↑ Exploration: Having a Good Attitude Is Important (February 21, 1995) Archived copy ( memento of the original from November 21, 2007 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (postponed unknown since 2007)
- ↑ Exploration: It's Such a Drag (February 21, 1995) Archived copy ( Memento of the original from July 15, 2007 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (postponed unknown since 2007)
- ↑ Exploration: Pitch, Yaw, and Roll Systems (October 3, 1995) Archived copy ( Memento of the original dated February 3, 2008 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (postponed unknown since 2007)
- ↑ Exploration: Inertial Reference Orbiter Attitude (October 3, 1995) Archived copy ( Memento of the original from July 14, 2007 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (postponed unknown since 2007)
- ↑ Exploration: Local Reference Orbiter Attitude (September 18, 1995) Archived copy ( Memento of the original from July 14, 2007 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice. (postponed unknown since 2007)