Tymoshenko beam

Deformation of a Tymoshenko bar (blue) compared to that of an Euler-Bernoulli bar (red)

The Timoshenko beam theory explained as part of the beam theory , the vibration behavior and the deflection clamped beams . The Tymoshenko beam theory was developed by the Ukrainian scientist and mechanic Stepan Tymoshenko at the beginning of the 20th century. It is important in large parts of classical mechanics , especially in buildings, bridges, etc., because here a beam should continue to fulfill its function even under the forces that occur; its behavior must therefore be predicted as precisely as possible.

The Tymoshenko beam theory extends the classic Euler-Bernoulli beam theory by an additional spatial derivation of the 2nd degree: in addition to the changed inertia of a deformed beam, shear deformation is also taken into account in the equation of motion .

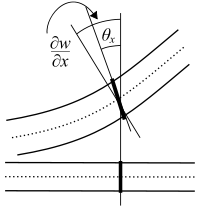
This means that Bernoulli's assumption that the cross-section of a beam remains perpendicular to the beam axis even after deformation is no longer fulfilled. Allowing additional (shear) deformation reduces the stiffness of the beam. This results in higher deformations and lower natural frequencies .

Static Tymoshenko beam

Deformation of a Tymoshenko beam. The normal rotates around , which is different from the curve of the beam axis. ${\displaystyle \theta _{x}=\varphi (x)}$ ${\displaystyle dw/dx}$

In the static Tymoshenko beam theory, the deflections of the beam are assumed to be

${\displaystyle u_{x}(x,y,z)=-z\cdot \varphi (x)}$

${\displaystyle u_{y}(x,y,z)=0}$

${\displaystyle u_{z}(x,y)=w(x)}$

in which

• ${\displaystyle (x,y,z)}$ the coordinates of a point on the bar (x: lengthways; y: front / back; z: vertical)
• ${\displaystyle u_{x},u_{y},u_{z}}$the components of the displacement vector in the three coordinate directions
• ${\displaystyle \varphi }$the rotation angle of the normal to the beam axis
• ${\displaystyle w}$represents the displacement of the beam axis in the direction. ${\displaystyle z}$

The static equilibrium results from the following system of uncoupled ordinary differential equations :

${\displaystyle {\begin{aligned}&{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\left(E\cdot I\cdot {\frac {\mathrm {d} \varphi }{\mathrm {d} x}}\right)=q(x,t)\\&{\frac {\mathrm {d} w}{\mathrm {d} x}}=\varphi -{\frac {1}{\kappa \cdot A\cdot G}}\cdot {\frac {\mathrm {d} }{\mathrm {d} x}}\left(E\cdot I\cdot {\frac {\mathrm {d} \varphi }{\mathrm {d} x}}\right)=\varphi -{\frac {Q}{\kappa \cdot A\cdot G}}\end{aligned}}}$

In it is

• ${\displaystyle E}$the modulus of elasticity of the beam material
• ${\displaystyle I}$is the area moment of inertia of the beam
• ${\displaystyle q}$the line load in the z-direction
• ${\displaystyle A}$the cross-sectional area of the beam
• ${\displaystyle G}$the shear modulus of the beam material.
• ${\displaystyle \kappa }$the Timoshenko shear coefficient which depends on the cross-section of the beam. Normally, for a rectangular cross-section = 5/6. ${\displaystyle \kappa }$

The combination of the two equations gives the equation for a homogeneous beam with constant cross-section : ${\displaystyle \left({\frac {\mathrm {d} E}{\mathrm {d} x}}={\frac {\mathrm {d} G}{\mathrm {d} x}}=0\right)}$ ${\displaystyle \left({\frac {\mathrm {d} A}{\mathrm {d} x}}={\frac {\mathrm {d} I}{\mathrm {d} x}}=0\right)}$

${\displaystyle E\cdot I\cdot {\cfrac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}=q(x)-{\cfrac {E\cdot I}{\kappa \cdot A\cdot G}}\cdot {\cfrac {\mathrm {d} ^{2}q}{\mathrm {d} x^{2}}}}$

Euler-Bernoulli bar as a special case of the Tymoshenko bar

The Tymoshenko beam theory can be converted into the Euler-Bernoulli beam theory if the last term is neglected. This is permissible for

${\displaystyle {\frac {E\cdot I}{\kappa \cdot A\cdot G\cdot L^{2}}}\ll 1}$

with the length of the beam. ${\displaystyle L}$

The Euler-Bernoulli beam theory can therefore be viewed as a special case of the Tymoshenko beam theory for high shear stiffness .

credentials

1. ↑ H. Bremer: Dynamics and Regulation of Mechanical Systems , Teubner Stuttgart 1988, p. 63
2. ^ F. Gruttmann and W. Wagner: Shear correction factors in Timoshenko's beam theory for arbitrary shaped cross sections (p. 9), Computational Mechanics 7 2001, p199-207