Intermodulation

The intermodulation ( IM or IMD ) refers to the formation of frequencies , when two or more different frequencies by a system with non-linear transfer function to be processed. The description using intercept points is used to characterize the non-linear properties of the transfer function . Intermodulations occur, among other things, in telecommunications systems such as amplifiers and acoustics due to non-linear transmission properties and are often undesirable in these applications.

Output spectrum of an amplifier with an electron tube , which is supposed to amplify the two frequencies 34 kHz and 653 kHz at the same time.

General

In the simplest case of two different frequencies and which are passed through a system with a non-linear transfer function, a sum of frequencies is formed through intermodulation, which are referred to as intermodulation products, in the form: ${\displaystyle f_{1}}$ ${\displaystyle f_{2}}$

${\displaystyle k_{1}\cdot f_{1}+k_{2}\cdot f_{2}}$

With than two whole numbers. The order in this case is the sum of the amounts . Some intermodulation products in the case of two frequencies are: ${\displaystyle k_{1},k_{2}}$ ${\displaystyle \ O}$ ${\displaystyle \left|k_{1}\right|+\left|k_{2}\right|}$

2nd order: ${\displaystyle f_{1}\pm f_{2}}$

3rd order: ${\displaystyle 2\cdot f_{1}\pm f_{2}}$

3rd order: ${\displaystyle f_{1}\pm 2\cdot f_{2}}$

4th order: ${\displaystyle 3\cdot f_{1}\pm f_{2}}$

4th order: ${\displaystyle f_{1}\pm 3\cdot f_{2}}$

5th order: ${\displaystyle 3\cdot f_{1}\pm 2\cdot f_{2}}$

5th order: ${\displaystyle 2\cdot f_{1}\pm 3\cdot f_{2}}$

${\displaystyle \dotsc }$

In the general case of frequencies, the resulting products are intermodulation products ${\displaystyle N}$

${\displaystyle \sum _{i=1}^{N}k_{i}\cdot f_{i}}$

The orders that arise are in the general case: ${\displaystyle \ O}$

${\displaystyle \ O=\sum _{i=1}^{N}\left|k_{i}\right|}$

Communications engineering

Frequencies of the 3rd order intermodulation products

Intermodulation products of two signals measured with a signal analyzer . The signals fed in are marked with markers 1 and 2 at frequencies and . Markers 3 and 4 are on the 3rd order intermodulation products ( and ). Furthermore, 5th order intermodulation products ( and ) can be seen. ${\displaystyle f_{1}}$ ${\displaystyle f_{2}}$ ${\displaystyle 2\cdot f_{1}-f_{2}}$ ${\displaystyle 2\cdot f_{2}-f_{1}}$ ${\displaystyle 3\cdot f_{1}-2\cdot f_{2}}$ ${\displaystyle 3\cdot f_{2}-2\cdot f_{1}}$

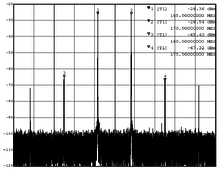
In communications engineering, the intermodulation products are caused by non-linearities in components such as diodes , voltage-dependent feedback capacitances in transistors or voltage-dependent resistances . These are desirable in additive mixers in order to generate combination frequencies.

Simplified for memoryless systems (i.e. the previous history does not matter here) the nonlinear transfer function can be written as

${\displaystyle y(t)=g[x(t)]}$

to be discribed.

Let g be any non-linear function, for example a quadratic function . As a result, the superposition theorem is no longer valid, since the various input signals influence each other. The intermodulation can be mathematically described by a Taylor series , provided the non-linearities are not too strong.

Approach with Taylor series

${\displaystyle u_{\mathrm {out} }(t)=k_{0}+k_{1}\cdot u_{\mathrm {in} }(t)+k_{2}\cdot {u_{\mathrm {in} }(t)}^{2}+k_{3}\cdot {u_{\mathrm {in} }(t)}^{3}+\dots +k_{n}\cdot {u_{\mathrm {in} }}^{n}}$

The larger the coefficients k ₂ and k ₃ , the smaller the 2nd and 3rd order intermodulation spacing.

The powers stand for 2nd order intermodulation, 3rd order intermodulation etc. This can be described mathematically with the help of addition theorems as follows: ${\displaystyle {u_{\mathrm {in} }}^{2}}$ ${\displaystyle {u_{\mathrm {in} }}^{3}}$

${\displaystyle {\cos }^{2}{x}={\frac {1}{2}}\cdot \left(\cos {2x}+1\right)}$

and

${\displaystyle {\cos }^{3}{x}={\frac {1}{4}}\cdot \left(\cos {3x}+3\cdot \cos {x}\right)}$.

If a two-tone excitation with the frequencies f ₁ and f ₂ now takes place, intermodulation products are obtained at the frequencies at the output of the circuit part described

${\displaystyle f_{m+n}=m\cdot f_{1}\pm n\cdot f_{2}}$,

where m and n are natural numbers, the sum of which corresponds to the order of intermodulation.

In signal transmission, 3rd order ( or ) intermodulation is undesirable because it falls within the useful frequency range and is difficult or impossible to filter out. ${\displaystyle 2\cdot f_{1}-f_{2}}$ ${\displaystyle 2\cdot f_{2}-f_{1}}$

Second order intermodulations (2 · f ₁ , 2 · f ₂ , f ₁  +  f ₂ and f ₂  -  f ₁ ) can also lead to interference, depending on the system structure.

Usually the intermodulation products with the order> 3 are strongly attenuated or can be easily filtered out due to the large distance to the useful frequency so that they do not play a major role in transmission technology.

Measures against intermodulation are e.g. B. the use of stages with high quiescent currents, which is not always possible with battery-operated devices. By reducing the modulation of the receiver or transmitter stages, an improvement is achieved, but at the expense of the input sensitivity or the transmission power.

Scalar measurement

Most of the power of the intermodulation signals (IM signals) are measured purely scalar. In other words, two signal generators are used as transmitters and a spectrum analyzer as a receiver. The device under test ( DUT ) is located between the generators and the receiver. In contrast to vector network analyzer measurements, no mismatches are calculated out. Furthermore, no phase information of the IM signals is available.

During these measurements, it must always be ensured that no IM signals are generated by the transmitter and / or receiver. For this purpose, narrowband bandpass filters must be used in the receiver, in particular, which prevent the powerful transmission signal from generating IM signals at the sensitive receiver due to its own nonlinearities. Whether a measured IM signal is generated by the DUT or in the receiver can be checked during the runtime of the measurement by increasing the input attenuator on the receiver. If all signal amplitudes are reduced by the same factor, the IM signals are from the DUT. If there is a change in the signal amplitudes depending on the order of the intermodulation, it is an IM signal generated by the receiver.

Vector measurement

As an alternative to the scalar measurement, the vector IM measurement can be carried out based on a vector network analyzer measurement. As a rule, this has much fewer measurement errors , since mismatches are automatically calculated out through a previous calibration . The decisive advantage of the vectorial measurement is that it can model the sources of interference. Even the position of the fault can now be calculated. In order to carry out this vectorial IM measurement, it is necessary to calibrate the network analyzer absolutely. The two additional calibration standards power sensor and comb generator are required for this. The Without Thru calibration method helps to calibrate two virtual gates using just one physical gate.

Occurrence

speaker

In loudspeakers , intermodulation is the typical distortion that becomes audible sooner or later at high bass levels depending on the quality of the loudspeakers. The transducer efficiency for high frequencies to be reproduced is periodically lower with the large amplitude naturally generated by low frequencies whenever the deflection is large - the voice coil then leaves the linear range of its deflection. The linear area is given by its protruding length compared to the air gap of the pole shoes.

In multipath systems, intermodulation can therefore normally only be effective in the frequency ranges that are radiated by the same chassis. Since distortions can be heard most clearly in the range of 500 Hz - 4 kHz and intermodulation is triggered most strongly by the large membrane excursion of low frequencies, 3-way loudspeaker boxes are built: bass (frequencies below a few 100 Hz) and mids (frequencies approx. 500 Hz – 4 kHz) are radiated with separate chassis, whereby the midrange is carefully protected from the air movement of the bass loudspeaker. 3-way systems are therefore clearly superior to 1-way and 2-way constructions in this regard. Nevertheless, the bass loudspeaker in a 3-way box must have a large range of linear deflection in order not to generate harmonics.

tuner

A quality feature of analog tuners is their selectivity and large signal strength. If this is not sufficient, there will be parallel reception of different transmitters or multiple reception of the same transmitter. This is often caused by mixing products that are caused by amplifier stages when these are not sufficiently intermodulation-proof.

In the VHF range, intermodulation of the 3rd order occurs, or especially in broadband cable networks, when many VHF radio programs are offered, the distances between the neighboring programs are small and often the same, e.g. B. 300 kHz, 350 kHz or 400 kHz each. If several equal distances follow one another, 3rd order intermodulation interference occurs on occupied frequencies, which is expressed in significantly increased noise, twittering or parallel reception even with correct leveling of the line and house connection amplifiers. The intermodulation takes place in the IF mixer of the VHF receiver itself and cannot be effectively prevented by the customer. The only alleviation would be a narrower pre-selection of the tuner, which does not allow at least one of the interfering partners to reach the mixer when receiving the desired program. ${\displaystyle 2\cdot f_{1}-f_{2}}$ ${\displaystyle 2\cdot f_{2}-f_{1}}$

An efficient remedy is only possible through a clever selection of the VHF cable frequencies: in any frequency window of at least 2, better 3 MHz, placed anywhere in the VHF range, there should never be identical intervals between individual VHF programs, i.e. H. Distances of z. B. 300 kHz - 300 kHz or 400 kHz - 400 kHz should just as little follow each other as z. B. 300 kHz - 400 kHz - 700 kHz. Outside the window of 2–3 MHz, the preselection of the tuner is sufficient to keep at least one of the interfering frequencies away from the mixer.

Cable network operators can rely on EDP-supported planning services from corresponding companies or manually determine functioning frequency assignments using a tabular planning aid from the headend manufacturer BLANKOM.

Radio microphones can also interfere with one another through intermodulation if the carrier frequency is not selected.

Inner ear (cochlea)

Intermodulation distortion occurs in the inner ear of mammals by the non-linear amplifying properties of the cochlea ( cochlea ) on. These distortions are perceptible and also measurable under certain circumstances. These so-called distorsively produced otoacoustic emissions ( DPOAE s) can be diagnosed and evaluated.

literature

• Wolfgang-Josef Tenbusch: Basics of the loudspeakers . 1st edition. Michael E. Brieden Verlag, Oberhausen 1989, ISBN 3-9801851-0-9 .
• Berndt Stark: Loudspeaker manual . 7th edition. Richard Pflaum Verlag, Munich 1999, ISBN 3-7905-0807-1 .
• Arndt Klingelnberg: TonmeisterTagung TMT conference report 2016 EN-1: Non-linear distortion revisited (english) . ISBN 978-3-9812830-7-5 .

Web links

• Free program for calculating the intermodulation products
• Program for calculating the intermodulation products in radio microphones
• Introduction to the measurement of intermodulation with derivation and information on practical measurement ( Memento from November 24, 2013 in the Internet Archive )
• Mixer script (PDF)

Individual evidence

1. ↑ Thalayasingam, K. and Heuermann, H., Novel Vector Non-Linear Measurement System for Intermodulation Measurements , European Microwave Conf., Rome, Oct. 2009.
2. ↑ Operating instructions for VHF headend manager BLANKOM FMB121. (No longer available online.) Archived from the original on September 16, 2016 ; accessed on September 5, 2016 . Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.  
3. ↑ http://www.shuredistribution.de/support_download/fachwissen/funksysteme/funk-intermodulation