syllogism

The syllogisms (from ancient Greek συλλογισμός syllogismós "[the] adding up ", "logical conclusion") are a catalog of certain types of logical conclusions. They form the core of the ancient logic of Aristotle , which emerged in the fourth century BC, and of traditional logic up to the 19th century. As the main technique of logic, the syllogistic approach was only replaced by the integration of logic into mathematics, in the wake of the work of George Boole and Gottlob Frege in the 19th and early 20th centuries.

Example of a valid syllogism

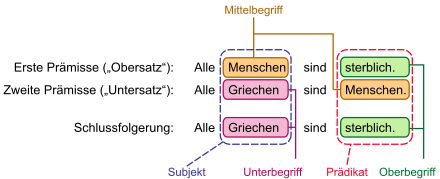
The teaching of syllogisms is generally referred to as syllogistics. Classical logic examined in particular the conditions under which syllogisms are valid . Syllogisms are always built according to the same pattern. Two premises (prerequisites), called major and minor , lead to a conclusion ( conclusion ). The premises and the conclusion are statements of a certain type in which one term, the syllogistic subject, is assigned or denied another term, the syllogistic predicate (not synonymous with subject and predicate in grammar ), in a certain way. Depending on the place at which they appear in the syllogism, the terms that occur are named generic term, middle term and subordinate term.

history

The Latin term syllogism goes back to the Greek syllogismos (συλλογισμός). With syllogismos Aristotle describes a deductive argument , which he is the first to define as follows:

"A deduction ( syllogismos ) is therefore an argument in which, if something has been posited, something other than what is posited necessarily results from the posited."

- Aristotle : Topic I 1, 100a25-27

In this broader sense, i.e. as a synonym for the word “argument”, the word “syllogism” was used in everyday language well into the 20th century. In modern parlance, this wide usage is no longer common and can only be found in expressions such as hypothetical syllogism (a collective term for certain propositional conclusions considered in tradition).

Confusingly, syllogism now only describes a special form of the deductive argument ( syllogismos ), namely the deduction dealt with in Aristotle's First Analytic , which consists of exactly two premises, one conclusion and three terms. Since the definition of deduction does not have this restriction, every syllogism us is a syllogism os , but not every syllogism os is a syllogism us .

According to the position of the middle term - that is, the term that occurs only in the premises - Aristotle differentiates between three types of inferences, called figures (see section Figures ). The introduction of a fourth figure, the conclusions of which Aristotle also recognizes as valid, is attributed by Avicenna and other Galen , although there is no direct reference to this attribution in Galen's traditional work and Galen actually expressly rejects it. Until the introduction of the fourth figure, its syllogisms are often assigned to the first figure in the tradition of Theophrastus of Eresus .

In the Latin Middle Ages, which initially took up the logical works of Aristotle from translations and commentaries by Boëthius , the traditional Latin terms for the quantity and quality of judgments (see section Types of Statements ) came into use by Petrus Hispanus . In scholasticism , syllogistics took on the form that was passed on for centuries in textbooks, although the authentic content of Aristotelian syllogistics had been lost since antiquity and it was subjected to increasingly harsh criticism since the Renaissance (the criticism by René is famous, for example Descartes ). It was only Jan Łukasiewicz who rediscovered Aristotle's logic in a groundbreaking work and axiomatically reconstructed it from the standpoint of modern logic; However, because of the large number of axioms applied, among other things, it is doubted that this reconstruction is sufficiently adequate to the subject. Łukasiewicz is followed by more recent research, which found its standard German work in Günther Patzig's presentation (1959).

Since then, a distinction has been made between the Aristotelian and traditional syllogistics. The most striking external difference is that Aristotle does not write down syllogisms as a sequence of three sentences, but as a sentence of the form “If (premise 1) and (premise 2), so necessary (conclusion)”; There is disagreement as to whether this formulation can be explained as a metalinguistic statement about a syllogism in the traditional understanding or whether it is to follow Łukasiewicz's view that Aristotle regards a syllogism as a compound statement. The two readings can easily be transferred into one another; The present article gives concrete syllogisms in the sense of the first reading consistently as a series of three sentences. Apart from this controversial point, there are numerous differences in the logical-semantic conception between Aristotelian and traditional syllogistics, so that today the view is often held that Aristotle is fundamentally much closer to modern logic than to traditional syllogistics. The conception of Aristotelian syllogistics, elaborated by Patzig among others, as the theory of certain two-digit relations between concepts and the relative product of such relations goes back to Augustus De Morgan . A syllogism is then a relation product, which is itself a relation in that particular form that is expressed in the four sentence types A, E, I or O (for A, E, I, O see types of propositions ).

The indiscriminate equation of Aristotelian and traditional syllogistics in the older historiography of logic ( Carl Prantl , Heinrich Maier ), on the other hand, has produced numerous errors - for example about the alleged metaphysical presuppositions of Aristotle's logic - from which the Aristotle interpretation was only able to free itself with difficulty.

General representation

Syllogistic arguments always follow the same pattern. Each two premises (conditions), called major premise (Latin propositio major ) and pedestal (Latin propositio minor ) lead to a conclusion ( Conclusion , Latin conclusio ). In the categorical syllogism (also called assertoric syllogism ) presented here, premises and conclusions are categorical judgments ; H. Statements in which a term (Greek ὅρος - horos , Latin terminus ), the subject, another term, the predicate, is assigned or denied in a certain way. For example, in the categorical judgment “All people are mortal”, the subject “human” is assigned the predicate “mortal”. It should be noted - and can be seen in this example - that the words “subject” and “predicate” are used differently in the context of syllogistics than in traditional grammar , where the grammatical subject is the expression “all people” and the grammatical predicate - each by perspective - the word "are" or the phrase "are mortal" would be.

A total of three different terms are used within a syllogism:

1. the generic term (Latin terminus major ) used in the major clause and on the right side of the conclusion, d. H. occurs as their predicate (P);
2. the sub-term (Latin terminus minor ) that appears in the sub-clause and on the left side of the conclusion, d. H. occurs as their subject (S); and
3. the middle term (M) (Latin terminus medius ), which occurs in the major and minor clause, but not in the conclusion.

In the succession of Johannes Philoponus , the terms “overarching term” and “subordinate term” have mostly been given no meaning in terms of content since the 17th century and they are explained exclusively from their appearance in the major or minor and as a predicate or subject of the conclusion. Occasionally, the sub-term and the generic term are also referred to as the subject or predicate of the syllogism.

An example of a valid syllogism is:

The middle term of this syllogism is the term "rectangle"; In the major clause of this syllogism the middle concept appears as a subject, in its minor clause as a predicate. The sub-concept of this syllogism is the term "square"; he appears in the sub-clause as a subject. The generic term for this syllogism is the term “circle”; it appears in the major clause as a predicate.

As an alternative to formulations such as “No S is P” or “All S are P”, expressions with the same meaning such as “P does not belong to any S” and “P corresponds to all S” are used. In this parlance, the above syllogism reads as follows:

The two spellings are synonymous and have the same value. While Aristotle himself in his analytics predominantly chooses variants of the second formulation, “P comes to all S” (mostly “τὁ P κατηγορεῖται τοῦ S” - “the P is stated about the S”), variants of the first notation have been used since scholasticism , "All S are P", given preference. The difference between grammatical and syllogistic subject or predicate is more evident in the Aristotelian formulation than in the traditional one; in the formulation “P comes to all S” has the syllogistic predicate, “P”, the function of the grammatical subject and the syllogistic subject, “S”, the function of the grammatical predicate.

However, in the follow-up to Jan Łukasiewicz there is the opinion that the Aristotelian syllogisms, in contrast to those of the tradition based on him, are not arguments from two premises and one conclusion, but rather compound individual sentences. From this point of view, the Aristotelian variant of the above example should read as follows:

If no rectangle is a circle and all squares are rectangles, then no square is a circle.

The correct classification of the Aristotelian syllogisms is still debatable today. Since the conversion between the two readings is simple and since Aristotle uses his syllogisms as a final rule despite their formulation in “if-then” form, the present article presents concrete syllogisms consistently in their traditional formulation as arguments composed of three statements.

As a further development of the categorical or assertoric syllogistics, there are approaches of a modal syllogistics already in Aristotle , in which modal statements such as "All people are possibly mortal" are permitted in the syllogisms - apart from this difference, which have the same structure.

Logical systems which, like syllogistics, work with statements in which concepts are related to one another are generally called conceptual logics.

Types of statements

A statement in a syllogism, a categorical judgment , always relates two concepts. Only four types of judgments regarding the relationship between a subject (S) and a predicate (P) are considered:

Type	designation	Formulations of the judgment	Shorthand
A.	generally affirmative judgment	all S are P (and there is indeed S) P belongs to all S.	SaP
E.	generally negative judgment	no S is P (and there actually is S) P does not belong to any S.	SeP
I.	particular affirmative judgment	some S are P P belongs to some S.	SiP
O	particular negative judgment	some S are not P P does not belong to some S.	SoP

The vowels come from the Latin words “ a ff i rmo” (I affirm) and “n e g o ” (I deny), whereby the first vowel stands for a general, the second for a particular judgment.

Quantity and quality

The property of a statement, how many objects it talks about, is traditionally called the quantity of that statement. In this sense there are two quantities in the syllogism, namely (a) particular and (b) universal or general. The property of a statement to assign or deny a predicate to a subject is traditionally called the quality of this statement. If a statement assigns a predicate to a subject, it is called an affirmative statement, if it denies it, it is called a negative statement. The types of statements are broken down in the following table according to their quality and quantity:

	affirmative	negative
general	A judgment	E judgment
particular	I judgment	O judgment

Logical square

The logical square

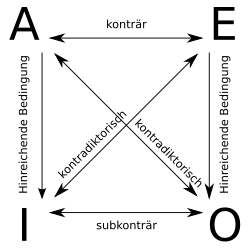
Assuming that their subjects are not empty concepts, there are different relationships between the different types of statements:

• Two statements form a contradictory opposition if and only if both can neither be true nor false at the same time, in other words: if both must have different truth values. This, in turn, is precisely the case if one statement is the negation of the other (and vice versa). For the syllogistic types of statements, the contradictory relationship applies to the pairs A – O and I – E.
• Two statements form a contrary opposition if and only if they cannot both be true at the same time, but both can be false. In the syllogistic only the statement pair A – E stands in contrary contrast.
• Two statements form a sub-contrarian opposition if and only if both cannot be false at the same time (but both can be true at the same time). In the syllogistic only the statement pair I – O is in sub-contradictory opposition.
• Between the types of statements A and I, on the one hand, and E and O, on the other hand, there is a corollary (traditionally this corollary is called a subalternation in the logical square ): From A follows I, i.e. i.e., if all are SP, then there are indeed S that are P; and from E follows O, i.e. i.e., if there are no SP, then there are indeed S that are not P.

These relationships are often summarized in a scheme known as the “Logical Square” (see illustration). The oldest known writing of the logical square comes from the second century AD and is ascribed to Apuleius of Madauros .

Existential requirements

As can already be seen in the logical square, many of the traditional laws of syllogistics only apply under the condition that at least the subject of the statements concerned is not empty. In general, therefore, it is assumed that syllogistic statements actually make statements about the existence of the subject; H. presuppose that the subject is not an empty concept:

• The statement “All S are P” means: “There are S, and all of them are P”.
• The statement “No S are P” means: “There are S, and none of them are P”.
• The statement "Some S are P" means: "There are S, and some of them are P."
• The statement "Some S are not P" means: "There are S, and some of them are not P."

The existence statement “There is S” is usually not understood as part of the respective syllogistic judgment, but as its presupposition , i.e. as a prerequisite for the respective judgment to be used at all for syllogistic inference. It is possible to make the statement about the existence of a part of the syllogistic judgment, but formally it is relatively complicated and is judged differently with regard to its adequacy.

Depending on the interpretation of the syllogistic statements and laws, it is also possible to see that syllogistic inference is only possible with non-empty terms, that is, the predicates must not be empty either. The question of which authors of the tradition represented which point of view is judged differently and is still the subject of philosophical and philological investigations.

Although existential prerequisites correspond to natural language usage (normally one only perceives general statements about actually existing things as meaningful), it is important to be aware of them, because there are also logical systems that do not make these prerequisites.

distribution

In syllogistics one speaks of the distribution (from Latin distributio , distribution) of a term within a statement. A concept is distributed within a statement if and only if every other statement follows from this statement that arises from the original statement by replacing the original concept with a real sub-concept. An often used and, if correctly understood, equivalent formulation reads: A term is distributed within a syllogistic statement if and only if it relates to all objects within the statement to which the term applies.

For example, in the syllogistic A-statement "All philosophers (subject) are people (predicate)" the term "philosopher" is distributed: From the fact that all philosophers are people, it follows that all language philosophers (a sub-term of "philosopher" ) People are that all existential philosophers (another sub-term of "philosopher") are people, etc. In this statement, however, the term "human" is not distributed: The fact that all philosophers are human does not mean, for example, that that all philosophers are Europeans (a sub-concept of human).

The following table gives an overview of which term is distributed in which type of statement.

	subject	predicate
A judgment	distributed	not distributed
I judgment	not distributed	not distributed
E judgment	distributed	distributed
O judgment	not distributed	distributed

Syllogisms from a modern point of view

There are different approaches to axiomatize traditional syllogistics or to build on clear rules.

The classical syllogisms can be represented in a modern way both as an application of a subsystem of predicate logic , namely the monadic predicate logic, and as set relationships. From today's point of view, an essential restriction is that the syllogisms can only deal with quantifiers that are connected to the subject of the statement (as in All people are mortal ), quantifiers in the object position (as in Socrates knows all Athenians ) cannot be treated in this system . This was only made possible by Frege's use of mathematical functions in logic.

When presented as quantity relationships, each term is interpreted as its scope ( extension in technical terms ), i.e. H. than the set of items that fall under this term. The term “human”, for example, is interpreted in set theory as the set of all people.

In the predicate logic interpretation, each term is represented as a one-digit predicate in the sense of the predicate logic, i.e. H. as a one-digit function in the mathematical sense that can be applied to concrete individuals and that provides information for each individual as to whether or not they fall under this term. For example, the term “human” would be interpreted as the predicate “_ is a human”. If one applies this predicate to a person, for example to Socrates, then it delivers the truth value “true”; if you apply it to an object that is not human - for example an animal, a planet or a number - then it yields the truth value "false".

Type	judgment	Set theory	Predicate logic
A.	All S are P.	${\displaystyle S\subseteq P}$, in which ${\displaystyle S\not =\emptyset }$ The (not empty) perimeter of S is a subset of the perimeter of P.	${\displaystyle \forall x(Sx\rightarrow Px)}$, in which ${\displaystyle \exists xSx}$ For every individual, if there is an S, then it is also a P (where S is not empty).
E.	No S are P.	${\displaystyle S\cap P=\emptyset }$, in which ${\displaystyle S\not =\emptyset }$ The intersection of the (non-empty) perimeter of S and the perimeter of P is empty.	${\displaystyle \forall x(Sx\rightarrow \neg Px)}$, in which ${\displaystyle \exists xSx}$ For every individual, if it is an S, then it is not the case that it is also a P (where S is not empty).
I.	Some S are P.	${\displaystyle S\cap P\neq \emptyset }$ The intersection of the perimeter of S and the perimeter of P is not empty.	${\displaystyle \exists x(Sx\wedge Px)}$ There is at least one individual who is an S and who is also a P.
O	Some S are not P.	${\displaystyle S\not \subseteq P}$ The (non-empty) scope of S is not a subset of the scope of P. (The fact that S cannot be empty is already implicitly given, since the empty set is a subset of every set.)	${\displaystyle \exists x(Sx\wedge \neg Px)}$ There is at least one individual who is an S and who isn't that is also a P.

This formalization has been criticized historically and recently. The traditional logic as conceptual logic, for example by Fritz Mauthner, was contrasted with modern logic, which was also disparagingly referred to as logistics . One of the central issues was whether formalization would lead to the loss of presuppositions of existence that were taken for granted in the premodern local tradition. A direct transfer of the logical square is also not without problems, as Michael Wolff has shown in his essay on Frege .

Walther Brüning classified the syllogistics as a strict syllogistics as a special case of his strict logic and in doing so encounters the problems of the classical formalization of predicate logic. He interprets the judgments as abbreviations of so-called validity value formulas (see: Categorical Judgment - Treatment in Strict Logic ) and uses a derivation term that allows all syllogisms to be derived easily. A similar approach is the differential syllogistic of Albert Menne .

Rules for the validity of syllogisms

Valid syllogisms have certain properties with regard to the quality, quantity, and distribution of the terms they contain; for example, a syllogism can never be valid if its premises are particular propositions but its conclusion is a general proposition.

Since different syllogistic modes are valid depending on the specific interpretation, there are also different sets of rules in the tradition. The most common rules today are presented below. In this simple form they go back to the late Middle Ages and are not part of the ancient, Aristotelian syllogistics. Said control system is redundant for the sake of simplicity, i. that is, some of the rules can be expressed by others.

Rules of quality

1. At least one of the two premises must be an affirmative statement ( Latin ex mere negativis nihil sequitur , “nothing follows from negative statements alone”).
   For example, no syllogistic conclusions can be drawn from the premises “No fish is an angler” and “Some anglers are not fish”.
2. If both premises are affirmative, then the conclusion must also be affirmative (Latin ambae affirmantes nequeunt generare negantem , "two affirmative statements cannot produce a negative statement").
3. If either of the two premises is negative, then the conclusion must also be negative.

Rules of quantity

1. At least one of the two premises must be a general statement (Latin nihil sequitur geminis ex particularibus unquam , "nothing ever follows from particular statements").
   From the premises “some mammals live in the water” and “some animals that live on land are mammals”, it is also not possible to draw conclusions from a syllogistic point of view.
2. If one of the two premises is a particular proposition, the conclusion cannot be a general proposition.

Distribution rules

1. The middle term must appear distributed at least once.
2. If a term appears distributed in the conclusion, it must also appear distributed in a premise.

characters

Which of the three terms S, P and M must appear in which statement of the syllogism is fixed: The major clause consists of P and M, the minor clause of S and M, the conclusion of S and P. The conclusion always has the form S - P, the arrangement of the terms in the premises can be chosen freely. The order in which the premises are written is irrelevant for the validity of a syllogism, but since Aristotle the major premise has been mentioned first and then the minor.

Depending on the arrangement of the terms in the premises, a distinction is made between the four possible figures (σχἠματα, schemata ):

	1st figure	2nd figure	3rd figure	4th figure
first premise	M - P	P - M	M - P	P - M
second premise	S - M	S - M	M - S	M - S
Conclusion	S - P	S - P	S - P	S - P

Example:

Premise 1 (or major premise ): All people (M) are mortal (P) .

Premise 2 (or minor ): All Greeks (S) are people (M) .

Conclusion (or conclusion ): So all Greeks (S) are mortal (P) .

Due to the position of the terms M - P, S - M, S - P one recognizes a syllogism of the first figure.

Modes (combinations) and their keywords

Since each of the three statements in a syllogism can be of one of the four types A, E, O, I, there are possibilities for each figure to combine statements to form a syllogism of the respective figure. Each of these possibilities is called a mode (plural: modes) or a combination of the respective figure. With a total of four different figures there are a total of possible combinations, i. H. 256 types of syllogisms. Among these 256 modes, 24 are valid and 232 are invalid syllogisms. ${\displaystyle 4\times 4\times 4=64}$ ${\displaystyle 64\times 4=256}$

A mode is described by three letters. The first two letters stand for the types of premises, the third letter for the type of conclusion.

Example:

Premise 1 (or major sentence ): All crime novels (M) are exciting (P) .

Premise 2 (or minor ): Some books (S) are crime novels (M) .

Conclusion (or final sentence ): So some books (S) are exciting (P) .

Premise 1 is of type A, premise 2 of type I, and consequently the conclusion is also of type I. It is therefore a syllogism of type A-I-I.

The 24 valid modes are traditionally designated with the following keywords:

1st figure: Barbara, Celarent, Darii, Ferio, Barbari, Celaront

2nd figure: Baroco, Cesare, Camestres, Festino, Camestrop, Cesaro

3rd figure: Bocardo, Darapti, Datisi, Disamis, Felapton, Ferison

4th figure: Bamalip, Calemes, Dimatis, Fesapo, Fresison, Calemop

In these memo words, the vowels denote the types of statements in the order major – minor – conclusion; for example, Modus Darii denotes a syllogism of the first figure and of type A-I-I. The consonants indicate to which syllogism of the 1st figure (first consonant) the respective syllogism can be traced back and through which change (consonant following the vowel) this tracing is possible (see section Reduction to the first figure ).

It should be noted that in the tradition different versions of the keywords circulate. The oldest surviving versions of this mnemonic syllogistic come from the scholastic logicians William of Sherwood and Petrus Hispanus around 1240/1250, the priority being uncertain.

The five modes that are not in bold are each “weak” consequences of a “strong” mode of the respective figure in bold. “Strong” means that the conclusion is a general statement (A or E); “Weak” means that the conclusion is a particular statement (I or O) that is a direct consequence of the strong statement in question. It is believed that weak modes first appeared in 50 BC. Were thematized by Ariston of Alexandria.

Examples:

• Modus Barbara (strong): All Munich residents are Bavarians, all Schwabingers are Munich residents, it follows: All Schwabingers are Bavarians.
• Modus Barbari (weak): All Munich are Bavarians, all Schwabing are Munich, it follows: Some Schwabing are Bavarians.
• Modus Celarent (strong): No Munich resident is Passau, all Schwabing residents are Munich, it follows: No Schwabing resident is Passau.
• Modus Celaront (weak): No one from Munich is Passau, all Schwabing are Munich, it follows: some Schwabing are not Passau.

The weak conclusions are logically valid if certain additional conditions are met: In each case, certain terms (subject, predicate or middle term) must not be empty (see also the section on existential requirements ).

Reduction to the first figure

With a few simple transformations, which are coded in the consonants of the traditional cues, the modes of all figures can be reduced to a mode of the first figure ("reduce"). This fact was already known to Aristotle, who also formulated corresponding rules of transformation and who described the first figure as the perfect, syllogisms of the first figure as the perfect syllogism (τέλειος συλλογισμός - téleios syllogismós ).

The first letter of the respective traditional keyword indicates the mode of the first figure the respective mode can be traced back to: Modes whose name begins with "B" can be traced back to the Barbara mode; Modes whose name begins with "C" can be traced back to the Celarent mode; and modes whose names begin with “D” or “F” can also be traced back to the Darii or Ferio mode.

The transformations of the syllogistics are rules of closure in the formal sense, i. That is, the result of every syllogistic transformation of a statement or a syllogism follows from the transformed statement or from the transformed syllogism.

The transformations required for the reduction are described in more detail below; In addition, in the section Examples and Reduction to the First Figure, an example is given for each syllogistic mode and its reduction to the first figure is shown.

Easy conversion

With the simple conversion (Latin conversio simplex ) the subject and predicate of the respective statement are interchanged; so the statement “some philosophers are Greeks” becomes after the simple conversion the statement “some Greeks are philosophers”. In the memo words, the simple conversion of a statement is indicated by the letter "s" after the vowel assigned to the statement concerned; for example, when reducing the Ce s are mode, the first premise, an E-statement, must undergo a simple conversion.

Simple conversion is only possible for statements of types E and I: If no pigs are sheep, then no sheep are pigs either (E statement); and if some Greeks are philosophers, then some philosophers are Greeks too (I-statement). No simple conversion is possible for the A- and O-statements: If all philosophers are people, that doesn't mean that all people are philosophers (A-statement); and if some people are not politicians, that does not mean that some politicians are not people (O-statement). In fact, there are only those traditional cue words in which the “s” follows an “e” or “i”.

Usually the simple conversion is applied to the particular premise of the syllogism being reduced. However, if the "s" is at the end of the cue word, then it is not the conclusion of the syllogism to be reduced that is subjected to the simple conversion, but the conclusion of the syllogism of the first figure to which the reduction is to be made. An example of this special case is the modus Dimati s : It is traced back to a modus datisi, in the conclusion of which subject and predicate are swapped, that is to a syllogism of the form “All P are M. Some M are S. So some are P S . "

Conversion by restriction

When converting through restriction (Latin conversio per accidens ), in addition to swapping subject and predicate of the respective statement, its type is changed from A to I or from E to O. For example, the A-statement “All pigs are pink” becomes the I-statement “Some pink (things) are pigs” after the conversion by restriction and the E-statement “No pigs are sheep” becomes the O-statement "Some sheep are not pigs". In the memo words, the conversion is indicated by the restriction by the letter "p" after the vowel assigned to the statement concerned.

With this conversion, too, there is a special case when the "p" in the noun comes after the third vowel - i.e. at the end of the word: In this case, as with the simple conversion, it does not refer to the conclusion of the syllogism to be reduced, but to the Conclusion of the resulting syllogism of the first figure.

Reversal of the premises

Interchanging the premises (Latin: mutatio praemissarum ) is necessary for the reduction of all those modes in which the consonant "m" occurs anywhere in the memo words. Regardless of the position of the consonant "m" in the respective keyword, the interchanging of the premises may only be carried out after every possibly necessary simple conversion and after every possibly necessary conversion by restriction.

Indirect evidence

Modes in which the consonant "c" occurs in the memo words, but is not at the beginning of the word - i.e. only the modes Baroco and Bocardo - can only be traced back to the first figure through an indirect proof (Latin reductio ad absurdum ). For this purpose, the truth of the A premise of the syllogism to be reduced (in the case of Baroco the first, in the case of Bocardo the second premise) as well as the adversarial opposite, i.e. H. assumed the negation of the conclusion. In this way a modus Barbara arises, the conclusion of which contradicts the O-premise of the syllogism to be reduced. Since the assumption that the conclusion does not apply has led to a contradiction in this way, it has been shown that the conclusion must be correct.

The indirect proof is detailed in the sections AOO - Modus Baroco and OAO - Modus Bocardo .

Different representations

With regard to the exact formulation of the conversion rules, there are differences between the individual authors; in particular, it is common to omit the results presented here a special case in the simple conversion and the conversion by limitation and the consonant "s" and "p" at the end of a word to be converted to refer syllogism and not - as shown here - to the Goal syllogism. However, this formulation would make it impossible to reduce the two modes “Bamalip” and “Camestrop” in the form shown, because conversion by restriction is not possible for either an I-statement or an O-statement.

Examples and reduction to the first figure

On the first figure of the categorical syllogism

The first figure has the following shape:

	Upper sentence: M - P
	Stand: S - M
It follows:	Conclusion: S - P

Your valid modes are Barbara, Celarent, Darii, Ferio, Barbari, and Celaront.

AAA mode Barbara

example

	All rectangles are squares
	All squares are rectangles
It follows:	All squares are rectangles

EAE - Modus Celarent

example

	No rectangle is a circle
	All squares are rectangles
It follows:	No square is a circle

AII - Modus Darii

example

	All squares are rectangles
	Some rhombs are squares
It follows:	Some rhombuses are rectangles

EIO - Ferio mode

example

	No mammal breathes with gills
	Some aquatic animals are mammals
It follows:	Some aquatic animals do not breathe through their gills

AAI - Modus Barbari

example

	All rectangles are squares
	All squares are rectangles
It follows:	Some of the squares are rectangles

annotation

Barbari is a derivative mode insofar as its conclusion is a weaker corollary of the conclusion of Modus Barbara: If all squares are rectangles, then in particular some squares are rectangles. Traditionally, a mode derived from another mode by weakening the conclusion is also referred to as a weak mode.

EAO - Modus Celaront

example

	No rectangle is a circle
	All squares are rectangles
It follows:	Some squares are not circles

annotation

Celaront's conclusion is a weakening of Celarent's conclusion: If no squares are circles, then in particular some squares are not circles either. Celaront is therefore traditionally referred to as a weak mode.

On the second figure of the categorical syllogism and its reduction to the first figure

The second figure has the following shape:

	Upper sentence: P - M
	Stand: S - M
It follows:	Conclusion: S - P

The valid modes of the second figure are Baroco, Cesare, Camestres, Festino, Camestrop and Cesaro.

AOO - Baroco mode

example

	All professors are serious
	Some lecturers are not serious
It follows:	Some lecturers are not professors

Reduction of the example to the first figure

The Baroco mode is one of only two modes in which the consonant "c" occurs in the noun, but is not at the beginning of the word. This constellation indicates that an indirect proof is required to trace back to the first figure. For this indirect proof, a syllogism is constructed, the first premise of which is the A-premise of the syllogism to be reduced - in the example the statement "All professors are serious." The second premise of the syllogism to be constructed is the contradictory negation of the conclusion of the syllogism to be reduced Syllogism used - in the example the statement “All lecturers are professors” (this A-judgment is the negative of the O-judgment “Some lecturers are not professors”, compare logical square ). Since the keyword “Baroco” begins with a “B”, the premises thus established are supplemented to form a syllogism of the Barbara modus, which then reads in full: “All professors are serious. All lecturers are professors. So all lecturers are serious. ”The conclusion that all lecturers are serious, however, is incompatible with the O-premise of the syllogism to be reduced, which just read“ Some lecturers are not serious ”. Thus it is shown that the assumption that the conclusion of the syllogism to be reduced does not apply leads to a contradiction. The conclusion of the syllogism to be reduced must therefore be correct, the syllogism to be reduced must therefore be valid.

EAE - Modus Cesare

example

	No mammal breathes through gills
	All fish breathe through gills
It follows:	No fish is a mammal

Reduction of the example to the first figure

The catchword “Cesare” begins with a “C”, the syllogism must therefore be traced back to a Modus Celarent. In the keyword “Cesare”, immediately after the “e”, which indicates the type of the first premise, there is the letter “s”, which requires the simple conversion of the statement concerned. If you simply convert the first premise, the statement "No gill breath is a mammal" arises. There are no other meaningful consonants in the keyword "Cesare", so the conversion is complete. In fact, the resulting syllogism is “No gill breath (M) is a mammal (P). All fish (S) breathe through gills (M). So no fish (S) is a mammal (P). ”A syllogism of the Celarent type.

AEE mode Camestres

example

	All fish breathe through gills
	No mammal breathes through gills
It follows:	No mammal is a fish

Reduction of the example to the first figure

The first letter "C" of the keyword "Camestres" indicates that the reduction must lead to a mode Celarent. The "s" after the vowel "e" of the second premise indicates that the premise must undergo a simple conversion; this creates the new statement "No gill breath is a mammal". Regardless of its specific position, the “m” indicates that the premises must be exchanged after any other possible transformations: The result is the syllogism “No gill breath is a mammal. All fish breathe through gills. So no mammal is a fish. "At the end of the word Camestres there is another" s ", which at this point requires a simple conversion of the conclusion of the target mode, i.e. the Celarent - and in fact the syllogism is" No gill breath is a mammal. All fish breathe through gills. So no mammal is a fish. ”A mode Celarent, in the conclusion of which the position of subject and predicate is reversed.

EIO - Festino mode

example

	No animal that breathes with gills is a mammal
	Some aquatic animals are mammals
It follows:	Some aquatic animals do not breathe through their gills

Reduction of the example to the first figure

The first letter "F" indicates that the syllogism can be traced back to a Modus Ferio. The letter "s" after the first vowel in the word "Festino" indicates that the first premise must be subjected to a simple conversion; this creates the new statement "No mammal breathes with gills". The keyword does not contain any other meaningful consonants, and in fact the syllogism resulting from this one transformation is “No mammal breathes with gills. Some aquatic animals are mammals. It follows: some aquatic animals do not breathe with gills. ”Of the expected type Ferio; the reduction is thus successfully completed.

On the third figure of the categorical syllogism and its reduction to the first figure

The third figure has the following shape:

	Upper sentence: M - P
	Base: M - S
It follows:	Conclusion; S - P

The valid modes of the third figure are Bocardo, Datisi, Disamis, Ferison, Darapti and Felapton.

OAO - Modus Bocardo

example

	Some people from Munich are not politicians
	All Munich residents are city dwellers
It follows:	Some city dwellers are not politicians

Reduction of the example to the first figure

The word "Bocardo" contains the consonant "c" inside the word, which indicates the need for indirect proof. A new syllogism is formed for this, the premises of which are the A premise of Bocardo - in the example the statement “All Munich residents are city dwellers” - and the negation of the Bocardo conclusion: If one negates the O-statement “Some city dwellers are not politicians ", Then the A-statement" All city dwellers are politicians ". Since the keyword “Bocardo” begins with a “B”, these two premises are arranged and supplemented with a conclusion that a syllogism of the form Barbara arises. For the example this syllogism is “All city dwellers are politicians. All Munich residents are city dwellers. So all Munich are politicians. ”The conclusion,“ All Munich citizens are politicians ”, contradicts the first premise of the syllogism to be reduced, the statement“ Some Munich citizens are not politicians ”; It has therefore been shown that the assumption that the Bocardo conclusion - that is, the statement "Some city dwellers are not politicians" - is wrong, leads to a contradiction - it must therefore be correct.

AII - Modus Datisi

example

	All rectangles are squares
	Some rectangles are squares
It follows:	Some of the squares are squares

Reduction of the example to the first figure

The keyword “Datisi” contains the letter “s” as the only meaningful consonant immediately after the vowel mark for the second premise; this must therefore be subjected to a simple conversion, i. i.e., their subject and their predicate must be exchanged. From this operation arises the syllogism “All rectangles are squares. Some squares are rectangles. So some of the squares are squares. ”This syllogism is of the form Darii, and the reduction is completed with it.

IAI - Modus Disamis

example

	Some fruits are apples
	All fruits are plants
It follows:	Some plants are apples

Reduction of the example to the first figure

The keyword "Disamis" indicates that for the reduction to a Modus Darii two simple conversions (letter "s" after the vowel denoting the respective statement), i.e. H. a swap of subject and predicate, as well as a swap of the premises (letter "m" anywhere) will be necessary. Simple conversions of the premises must always be carried out before a possible exchange. “Disamis” calls for the simple conversion of the first premise, resulting in the sentence “Some apples are fruit”. For the second premise, the keyword “Disamis” does not require any action, so that in the next step the premisses (letter “m”) can be swapped. The resulting syllogism is “All fruits are plants. Some apples are fruits. So some plants are apples. ”In the last position - immediately after the vowel that denotes the conclusion - the word“ Disamis ”contains another“ s ”. The conversion of the conclusion - whether simple or by restriction - is a special case, because what is meant here is not the conclusion of the syllogism to be reduced, but the conclusion of the mode to which the reduction is to take place. The "s" at this point is the instruction to exchange subject and predicate in the conclusion of Modus Darii, which leads to a syllogism of the form "All M are P. Some S are M. So some are P S." This is the form of the reduced Disamis syllogism: “All fruits (M) are plants (P). Some apples (S) are fruits (M). So some plants (P) are apples (S). ”This completes the reduction.

EIO - Ferison mode

example

	No people from Munich are from Passau
	Some people from Munich are students
It follows:	Some students are not from Passau

Reduction of the example to the first figure

The catchword "Ferison" contains only one meaningful consonant, the "s" immediately after the vowel for the second premise. This indicates that the second premise needs a simple transformation, i.e. H. an exchange of their subject and their predicate. The resulting syllogism, “No people from Munich are Passau. Some students are from Munich. So some students are not from Passau. ", Is already a syllogism of the first figure, namely - the term" Ferison "begins with an" F "- of the Ferio type.

AAI - Darapti mode

example

	All squares are rectangles
	All squares are rectangles
It follows:	Some of the squares are rectangles

annotation

The Modus Darapti assumes that the subject is not empty, that is, that there are actually squares in the example; see section Existential Requirements .

Reduction of the example to the first figure

The first letter of the word "Darapti" indicates that the syllogism can be reduced to the Modus Darii. The word “Darapti” only contains the “p” of meaningful consonants, which denotes a conversion by restriction. The “p” is immediately after the vowel of the second premise, so it is this that needs to be converted by restriction. When converting through restriction, the subject and predicate of the sentence are exchanged and the quantity of the statement is changed from general to particular, so the statement "All squares are quadrilaterals" results in the statement "Some squares are squares". Since there are no other meaningful consonants in the term “Darapti”, the reduction is completed at this point and the resulting syllogism is “All squares are rectangles. Some of the squares are squares. So some squares are rectangles. ”A Modus Darii.

EAO - Modus Felapton

example

	No people from Munich are from Passau
	All Munich residents are city dwellers
It follows:	Some city dwellers are not from Passau

annotation

The Felapton mode presupposes that the middle term is not empty, i.e. that there are actually Munich residents in the example; see section Existential Requirements .

Reduction of the example to the first figure

Modus Felapton can be reduced to a Modus Ferio with a conversion by restriction (letter "p"). The “p” in the word “Felapton” is behind the vowel that denotes the second premise; therefore it is she who must be transformed. When converting by restriction, subject and predicate of the general statement concerned are exchanged and it is converted into a particular statement: “All Munich residents are city residents” becomes “Some city residents are Munich residents.” The resulting syllogism, “No Munich residents are Passau. Some of the city dwellers are Munich residents. So some of the city dwellers are not from Passau. ”Is in the form of the Modus Ferio - the reduction is thus complete.

On the fourth figure of the categorical syllogism and its reduction to the first figure

The fourth figure has the following shape:

	Upper sentence: P - M
	Base: M - S
It follows:	Conclusion: S - P

The valid modes of the fourth figure are Calemes, Dimatis, Fresison, Bamalip, Calemop and Fesapo.

AAI - mode Bamalip

example

	All squares are rectangles
	All rectangles are squares
It follows:	Some of the squares are squares

annotation

The Bamalip mode assumes that the subject is not empty, that is, that there are actually squares and rectangles in the example (the existence of the latter in this case already follows from the existence of the former); see section Existential Requirements .

Reduction of the example to the first figure

For the premises, the keyword “Bamalip” only has one instruction ready to swap their order (consonant “m” anywhere). The second meaningful consonant inside the word is the "p", which leads to a conversion by restriction - i. H. an exchange of subject and predicate of a statement as well as their change of their quantity from general (A, E) to particular (I, O) - prompts. Now the “p” is at the end of the word - this is the special case in which the conclusion of the syllogism to be reduced does not have to be converted, but the conclusion of the syllogism to which the reduction is to take place. Should be reduced - the keyword "Bamalip" begins with "B" - to Barbara, and if one subjects his conclusion, "All S are P", to a conversion through restriction, it reads "Some P are S". The syllogism "All M are P. All S are M. So some are P S." thus created from Modus Barbara corresponds exactly to the transformed syllogism Bamalip, "All rectangles (M) are quadrilaterals (P). All squares (S) are rectangles (M). So some squares (P) are squares (S). ”Bamalip is thus reduced to the first figure.

AEE - Calemes mode

example

	All of Passau are Bavarians
	No Bavarians are Saxons
It follows:	No Saxons are from Passau

Reduction of the example to the first figure

It is reduced to a mode Celarent, as the first letter of the keyword "Calemes" indicates. The last vowel in “Calemes” is followed by the meaningful consonant “s”, which requests a simple conversion of the conclusion in the syllogism to which it is to be reduced. If you convert the mode Celarent accordingly, i. That is, if you swap subject and predicate in your conclusion, the result is the mode “None M are P. All S are M. So none are P S.” Modus Calemes can be reduced to this - the only other meaningful consonant in The catchword “Calemes” is the “m” - by reversing its premises. The resulting syllogism is of the desired shape: “No Bavarians (M) are Saxons (P). All Passau (S) are Bayern (M). So there are no Saxons (P) Passau (S). "

IAI - Modus Dimatis

example

	Some rhombuses are rectangles
	All rectangles are parallelograms
It follows:	Some parallelograms are lozenges

Reduction of the example to the first figure

It is reduced to Darii, as the first letter of the keyword "Dimatis" indicates. The "m" calls for the premises to be reversed. The "s" at the end of the word shows the need for a simple conversion - i. H. Exchanging subject and predicate - the conclusion of the goal syllogism, i.e. the Darii. In fact, the resulting syllogism has the shape of a modus Darii with the premise transformed as follows: “All rectangles (M) are parallelograms (P). Some rhombuses (S) are rectangles (M). So some parallelograms (P) are diamonds (S). "

EAO - Modus Fesapo

example

	Munich residents are not from Passau
	All Munich residents are city dwellers
It follows:	Some city dwellers are not from Passau

annotation

The Modus Fesapo assumes that the middle term is not empty, that in the example there are actually Munich residents; see section Existential Requirements .

Reduction of the example to the first figure

In order to reduce the syllogism to a modus Ferio (the word "Fesapo" begins with an "F") the first premise must be subjected to a simple conversion (immediately after the first vowel in the word "Fesapo" there is an "s") and must be the second premise are subject to a transformation through restriction (immediately after the second vowel in the word “Fesapo” there is a “p”). The resulting syllogism is actually of the Ferio type: “No Munich (M) are Passau (P). Some city dwellers (S) are Munich (M). So some city dwellers (S) are not Passau (P). "

EIO - Fresison mode

example

	Munich residents are not from Passau
	Some people from Munich are students
It follows:	Some students are not from Passau

Reduction of the example to the first figure

In order to reduce a mode Fresison to the first figure, both premises must be subjected to a simple conversion, because the word Fresison contains the consonant "s" both immediately after the first vowel and immediately after the second vowel. Further meaningful consonants are not included, so that the syllogism resulting from these two conversions already has the form of a Modus Ferio (the mnemonic “Fresison” begins with an “F”) of the first figure: “No Munich (M) are Passauers (P) . Some students (S) are from Munich (M). So some students (S) are not Passau (P). "

Substantially different syllogisms

The equivalences "XeY exactly if YeX" and also "XiY exactly if YiX" make it possible to identify syllogisms in several pairs, in the EIO case even four, through all four figures. Then there is a shortened list of only eight syllogisms left in the event that weaknesses are deleted: Barbara, Darii, Felapton, Ferio, Camestres, Celarent, Bocardo and Baroco.

See also

• Conceptual logic
• Syllogisms in traditional rhetoric :
  • Enthymeme - a conclusion partly understood as a syllogism, often in a shortened representation
  • Epicherem - syllogism in which each premise is in turn an abbreviated syllogism
• Subsumtion - syllogism in legal work

literature

• Aristotle: First Analytics I . Aristotle: Analytica Priora. Book I. Translated and explained by Theodor Ebert and Ulrich Nortmann. Berlin: Akademie Verlag, 2007 ISBN 978-3-05-004427-9 (with extensive commentary)
• Aristotle: Analytica Posteriora . Translation and commentary by Wolfgang Detel . Berlin, Akademie-Verlag 1998. ISBN 3-05-001796-1 . (with extensive commentary)
• Aristotle: Organon . Greek-German. Translation and commentary by HG Zekl. 4 parts in 3 volumes, Meiner 2001, ISBN 3-7873-1596-9 . (The translation was criticized extremely sharply as unusable when it was first published; cf. the review by Hermann Weidemann in: Zeitschrift für philosophische Forschung  53, 1999, pages 602–610)
• Aristotle: Topic . Ditzingen: Reclam 2004. (= Reclams Universal Library 18337) ISBN 3-15-018337-5 , ISBN 978-3-15-018337-3 .
• Helmut Gätje : Comments on the system of syllogisms . Saarland University , Oriental Studies, Saarbrücken 1978.
• Bruno von Freytag-Löringhoff : About the system of modes of the syllogism . In: Journal for Philosophical Research . Vol. 4, No. 2/1949, pp. 235-256.
• Günther Patzig : The Aristotelian syllogistics. Logical-philological investigation into Book A of the “First Analytics” . 3rd edition, Göttingen, 1969.
• Albert Menne : Logic and Existence . (A logistic analysis of the categorical syllogism functors and the problem of the null class) Meisenheim 1954.
• Michael Wolff : Treatise on the principles of logic. With a reconstruction of the Aristotelian syllogistics . Second, improved and expanded edition, Frankfurt am Main: Klostermann 2009. ISBN 978-3-465-03639-5 .
• in English:
  • Otto Bird: Syllogistic and Its Extensions , Englewood Cliffs: Prentice-Hall 1964. (simple illustration)
  • William Kneale , Martha Kneale : The Development of Logic , Clarendon Press 1962. ISBN 0-19-824773-7 . (Standard work on the history of logic)
  • Jan Łukasiewicz : Aristotle's Syllogistic from the Standpoint of Modern Formal Logic , Oxford: Clarendon Press ² 1957, then Taylor & Francis 1987, ISBN 0-8240-6924-2 . and Oxford University Press 1998 (= Oxford University Press Academic Monograph Reprints), ISBN 0-19-824144-5 . (Standard work of modern research on syllogism)
  • Paul Thom: The Syllogism , Munich: Philosophia 1981, ISBN 3-88405-002-8 .

Web links

Commons : Syllogisms  - collection of images, videos, and audio files

Wiktionary: syllogism  - explanations of meanings, word origins, synonyms, translations

• Robin Smith:  Aristotle's Logic. In: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy .
• Henrik Lagerlund:  Medieval Theories of the Syllogism. In: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy .
• Terence Parsons:  The Traditional Square of Opposition. In: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy .
• Niko Strobach: Newer interpretations of the Aristotelian syllogistics (PDF; 112 kB)
• Edward D. Buckner. (Ed.): Square of Opposition (collection of texts, English)
• syllogistic online program
• Computational Aristotelian Term Logic ( Memento from July 17, 2009 in the Internet Archive ) - extensive online syllogistic program in English

Individual evidence

1. ^ Translation of Wagner / Rapp
2. ↑ Thus, different still Meyers Large conversation Encyclopedia 1905-1909 between the syllogism in the wider sense ( "in logic, in general, the circuit at all" - Volume 19, page 234) from the syllogism in the strict sense (the "categorical S [STATEMENTS] , the syllogism of Aristotle ”- Volume 17, page 877).
3. ↑ ^{a b} "Logic", in: The New Encyclopaedia Britannica , Chicago a. a. 15th edition 2003, volume 23, page 263
4. ↑ Albert Veraart: Pharmaceutical figure, in: Jürgen Mittelstraß: Encyclopedia philosophy and philosophy of science. Metzler Stuttgart 1996, ISBN 3-476-02012-6 , 1st volume, page 699
5. ^ "Logic", in: The New Encyclopaedia Britannica , Chicago a. a. 15th edition 2003, volume 23, page 265
6. ↑ N. I. Kondakow: Dictionary of logic. VEB Bibliographisches Institut Leipzig 1st edition 1978, page 410
7. ↑ Jan Łukasiewicz : Aristotle's Syllogistic from the Standpoint of Modern Formal Logic , Oxford: Clarendon Press ² 1957.
8. ^ "The result [of Łukasiewicz's] is something of great interest, but very different from Aristotle's own conception of his work" ( Kneale / Kneale: The Development of Logic, page 80)
9. ^ Günther Patzig: The Aristotelian Syllogistics. Logical-philological investigation into Book A of the “First Analytics” . 3rd edition, Göttingen, 1969.
10. ↑ Niko Strobach: Newer interpretations of the Aristotelian syllogistics (PDF; 112 kB), page 13, in particular the Prior quotation "The Prior Analytics ... is not a book of syllogisms, but a book about syllogisms, and the statement" If B is predicable of every M, and M of every A, then B is predicable of every A 'is a perfectly natural way of talking about syllogisms of the form' Every B is M, and every M is A, therefore etc. ' , and saying that all such syllogisms are valid. "
11. ^ Gereon Wolters: Syllogistik, in: Jürgen Mittelstraß: Enzyklopädie Philosophie und Wissenschaftstheorie. Metzler Stuttgart 1996, ISBN 3-476-02012-6 , 4th volume, page 156-158, page 157, column 2
12. ↑ An example of this view is the Duden grammar from 1966 (Duden Volume 4, 2nd edition 1966, § 6020 c, page 540), which regards the word “mortal” in this context as a form of supplementary circumstance, more precisely than Specification (§ 5280, page 481): "However, it is also a species addition where the specification of the species follows the 'copulative' verbs, because in these cases we also assign it the value of an independent sentence member [.]" (§ 5285 , Page 481) or "Newer views also assign [the copula verbs] the same rank [of a predicate]" (§ 5125, page 473)
13. ↑ An example of this view is the current Duden grammar: “Predicative verbs combine with a subject or object predicative to form a multipart predicate. These include the so-called copula inheritance [wie] sein "(Duden Volume 4, 7th edition 2005, § 577, page 421)
14. ^ "Since the seventeenth century most writers have adopted the suggestion of John Philoponus that the major term be defined as the predicate of the conclusion" (Kneale / Kneale: The Development of Logic, page 71)
15. ^ "[I] t would probably be a mistake to lay much emphasis on the distinction. For in the detailed application of his theory Aristotle reasons as though his conditional statements were in effect rules of inference rather than theses. "(Kneale / Kneale: The Development of Logic, page 80)
16. ^ Christian Thiel: Logical square , in: Jürgen Mittelstraß (Ed.): Encyclopedia Philosophy and Philosophy of Science. 1st edition 1995, 2004, volume 3, page 423
17. ↑ see e.g. B. Niko Strobach: Newer interpretations of the Aristotelian syllogistics (PDF; 112 kB), page 5f.
18. ^ "In order to justify Aristotle's doctrine as a whole it is necessary, then, that he assumed application for all the general terms with which he dealt." (Kneale / Kneale: The Development of Logic, page 60, emphasis in the original)
19. ↑ This variant of the definition is borrowed from "Distribution", in: Encyclopaedia Britannica , Volume 4, 15th ed. 2003, page 129
20. ↑ see Bird 1964, pp. 20-22
21. ^ "A simple set of rules of validity was finally produced in the later Middle Ages, based on the concept of Distribution." ( CL Hamblin : Fallacies. Methuen London 1970, ISBN 0-416-70070-5 , page 195)
22. ↑ see CL Hamblin: Fallacies. Methuen London 1970. ISBN 0-416-70070-5 , page 117, where, however, it is pointed out in footnote 1 that there are forerunners.
23. ↑ Kneale / Kneale: The Development of Logic, pp. 231-234
24. ↑ The presentation of the indirect proof in the syllogism follows very closely “Logic”, in: The New Encyclopaedia Britannica , Chicago a. a. 15th edition 2003, volume 23, page 262f.
25. ↑ z. B. also in the standard textbook Otto Bird: Syllogistic and Its Extensions , Englewood Cliffs: Prentice-Hall 1964, page 27ff.

This version was added to the list of articles worth reading on November 27, 2006 .