Problem of the museum guards

The problem of the museum guard ( en : Art gallery problem ) is a question of algorithmic geometry . The following situation is examined:

“Given a polygonal area with a border , interpreted as the floor plan of a museum. Now choose as few points as possible ("watchers") inside the polygon, so that every point inside the polygon can be connected to a watcher by a straight line that lies entirely within and including the edge. " ${\ displaystyle G}$ ${\ displaystyle \ partial G}$ ${\ displaystyle p_ {1}, p_ {2} \ dots p_ {k}}$ ${\ displaystyle G}$

This is equivalent to covering a polygon in a minimal star shape .

In practice, the problem arises in robotics when “ artificial intelligences ” are supposed to execute movement patterns depending on their surroundings. Some issues in digital image processing can be traced back to guard problems. Lighting problems of a stage and the problem of observing animal populations in large areas can also be modeled as guardian problems. Another application is the setting up of the infrastructure for weather observation or for warning of natural disasters.

In terms of complexity theory , the problem falls into the class of APX problems, which means that there is probably no algorithm that solves it efficiently and correctly for general polygons . On the other hand, upper bounds for the number of guards have been found for the problem and its variants and have been able to prove that these are also sharp. This means that they cannot be further improved without restricting yourself to special polygon classes.

Victor Klee suggested what was probably the first systematic consideration of questions of visibility at a conference in Stanford in August 1973, when he formulated the museum problem for point guards and a guesswork that turned out to be correct. Two years later, Chvátal presented a proven solution to the problem.

Elementary examples

We will first consider the "simple" version of the stationary guard problem. For a given small number of edges, consider a polygon that requires as many guards as possible. With a triangle and a square you have few options because obviously one guard is always sufficient. In the case of a pentagon, this is still correct, although this insight is no longer so obvious: ${\ displaystyle n}$

Special case of 5-sided polygons
illustration 1
Figure 2
Figure 3
Figure 4

The first three figures show stereotypes of all possible pentagons: Each pentagon can either have no, one or two concave corners, i.e. corners that have an interior angle of more than 180 ° or in radians . This follows from the fact that in every corner the sum of the interior angles is equal , in this case this sum is . So it allows a maximum of two concave corners. ${\ displaystyle \ pi}$ ${\ displaystyle n}$ ${\ displaystyle \ pi (n-2)}$ ${\ displaystyle n = 5}$ ${\ displaystyle 3 \ pi}$

For the 4th example you would need two guards: one on one of the points of contact of the triangles and another in the remaining triangle. However, one would complain there that the polygon "actually" has nine sides if one wanted to prohibit overlapping. Usually you do that too. From now on only such intersection-free polygons are considered.

Further "critical graphs" for small numbers of edges
Figure 5
Figure 6
Figure 7
Figure 8

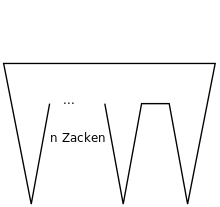
In the case (Figures 5 and 6) the case arises that there are polygons that cannot be guarded by one guard alone, but two guardians are always sufficient. If one continues such considerations, one can observe that after every three further edges a further guard may be necessary. A polygon that requires a maximum number of guards for a number of edges is called a critical polygon in the context of the problem . ${\ displaystyle n = 6}$

Chvátal's Theorem

The proof that the above examples are actually critical polygons, i.e. that three or four guards are always sufficient for nine or twelve-sided polygons, is a special case of the following sentence:

"To guard any non-overlapping, closed and planar polygon with sides, guard points are always sufficient and sometimes necessary." ${\ displaystyle n}$ ${\ displaystyle \ left \ lfloor {\ frac {n} {3}} \ right \ rfloor}$

- Vašek Chvátal (1975) :

As a proof, there are essentially two versions: A geometric variant, as Chvátal initially stated, and a graph-theoretical variant , which was given by S. Fisk. Fisk's proof uses some well-known results from graph theory , so the proof is comparatively short and is considered a little more aesthetic. On the other hand, in contrast to Chvátal, he does not allow some generalizations.

proof: (According to Fisk) For a closed, planar and non-intersecting polygon, suitable chords can be drawn between its corners, so that the polygon breaks down into pairs of disjoint triangles , except for the chords . Such a decomposition is obviously called triangulation and its existence is generally proven under the given conditions. It is also known that the corners of a triangulated polygon can be colored using only three colors so that adjacent corners have different colors. Each color class is then obviously a valid sentinel set; This is especially true for the smallest color class that contains straight corners. ${\ displaystyle \ left \ lfloor {\ frac {n} {3}} \ right \ rfloor}$

Even before this theorem was proven, it was known that this upper bound could not be tightened any further if it were found to be valid. To do this, consider the following sequence of graphs with edges. Every such polygon needs guards. ${\ displaystyle G_ {n}}$ ${\ displaystyle 3n}$ ${\ displaystyle n}$

Based on Fisk's design evidence, Avis and Toussaint developed an algorithm that constructs a guard set of size . Its running time essentially depends on how efficiently a triangulation can be found. Some simple methods do this in quadratic time. In their article they propose a version in . In 1990 Chazelle introduced a runtime algorithm . ${\ displaystyle \ left \ lfloor {\ frac {n} {3}} \ right \ rfloor}$ ${\ displaystyle {\ mathcal {O}} (n \ log n)}$ ${\ displaystyle {\ mathcal {O}} (n)}$

The coloring is then relatively easy to construct if one assumes that the triangulation transfers a data structure that contains all the adjacency information. Generally this cannot be secured. The achievement of Toussaint and Avis was to find a coloring in linear time using only a list of chordal edges of triangulation.

Variants and generalizations

Orthogonal polygons

An essential special case of the guard problem is the restriction to orthogonal polygons . This is understood to be polygons that only assume the interior angles and that are 90 ° or 270 °. Such polygons are considered in geometric applications that are strongly tied to the Cartesian coordinate system : these include design problems of highly integrated circuits , architecture and some algorithms on raster graphics . ${\ displaystyle {\ frac {\ pi} {2}}}$ ${\ displaystyle {\ frac {3 \ pi} {2}}}$

The initially obvious assumption that with this restriction one would be able to prove a better limit to the number of necessary guards was confirmed in 1980 by a theorem by Klawe and Kleitman . They showed the existence of so-called “ convex quadrilaterations ”: These are, analogous to triangulation, the decomposition of a polygon into convex quadrilaterals by drawing chords between certain corners that lie entirely within the polygon. Your proof of this is kept very general and holds for a corresponding statement about polygons with (finitely many) "holes" or "overlaps". It can be shown comparatively easily that the dual graph of a convex quadrilateration cannot contain any of the Kuratowskiminoren, i.e. the graphs and . According to Kuratowski's theorem , the graph is then planar and four- colorable according to the four - color theorem. From this follows the sentence: ${\ displaystyle K_ {5}}$ ${\ displaystyle K_ {3,3}}$

"Guard points are always sufficient and sometimes necessary to guard any overlapping and hole-free as well as planar and orthogonal polygons with sides ." ${\ displaystyle n}$ ${\ displaystyle \ left \ lfloor {\ frac {n} {4}} \ right \ rfloor}$

- Theorem by Klawe and Kleitman (1983)

That guards are sometimes necessary is shown by analogy, for example, with the general case of the "orthogonal comb": ${\ displaystyle \ left \ lfloor {\ frac {n} {4}} \ right \ rfloor}$

To show the existence of the convex quadrilaterations, the proof uses the following concepts that build on one another:

A “right” and a “left” edge and a polygon are called adjacent , if ${\ displaystyle R}$ ${\ displaystyle L}$ ${\ displaystyle G}$

The inside of "left" of and right of lies. ${\ displaystyle G}$ ${\ displaystyle R}$ ${\ displaystyle L}$
${\ displaystyle R}$ and "see" each other (that is, there are points and , so that the connection is entirely contained in.) ${\ displaystyle L}$ ${\ displaystyle r \ in R}$ ${\ displaystyle l \ in L}$ ${\ displaystyle rl}$ ${\ displaystyle G}$
The distance between and to one another is minimal under the conditions (1) and (2). ${\ displaystyle R}$ ${\ displaystyle L}$

From this it follows immediately that no neighbor has to exist for an edge, but if one does exist, it can be assumed that it is unique. If two adjacent edges are connected by a vertical edge, the three edges together are called an ear . For "upper" and "lower" edges, the neighborhood and ear properties are defined quite analogously.

Finding such ears in given polygons is interesting because it is relatively easy to prove that every convex quadrilateration must contain every ear. However, in order to get the statement of the guard theorem, one has to grasp the concept somewhat more generally, because not every polygon has to contain an ear.

In addition, there are those (ear-containing) polygons which allow a polygon to be reduced by splitting off a convex quadrilateral to one or more smaller ones, that is to say with at least one hole or one less edge, and those which do not allow such a reduction. These are called reducible or irreducible . Klawe and Kleitmann were able to show that orthogonal polygons

are either reducible in this sense
or a pair of ears (two ears so that the connecting edges of the adjacent edges see each other),
or contain two adjacent edges that do not form an ear,
or have to have an infinite number of corners.

For the case of the pair of ears and the neighboring edges, they could also specify a reduction to a smaller polygon and thus inductively establish the existence of the proposed quadrilaterations for finite polygons.

Examples of convex quadrilaterations

Convex quadrilaterations of orthogonal polygons are generally ambiguous. This polygon has no ear.

The square is an ear. is no ear because with adjacent. The convex quadrilateration (shown), which is unique in this case, cannot be constructed from a general triangulation. (could contain the triangle ) ${\ displaystyle \ {6,7,8,9 \}}$ ${\ displaystyle \ {2,3,4,5 \}}$ ${\ displaystyle \ {2,3 \}}$ ${\ displaystyle \ {6.7 \}}$ ${\ displaystyle \ {2,6,9 \}}$

Algorithms

Sack presents an attempt to implement the proof just presented in his doctoral thesis from 1984.

Lubiw developed a different proof approach and an algorithm derived from it in 1985.

Fortress problem

Independently of one another, Derick Wood and Joseph Malkelvitch asked in the 1970s about two generalizations of the problem of museum guards: instead of finding points guarding the inside of a polygon, they asked about points guarding the outside, or doing both. Wood coined the names fortress problem (for guarding problems of outer areas) and problem of the prison yard (for problems in which both should be guarded). The fortress problem has been satisfactorily solved in that it was possible to prove clear statements about the number of guards required for a polygon in the number of corners.

This orthogonal polygon according to Argawall needs guards for corners to guard the outside area.

{\ displaystyle n = 24}

{\ displaystyle 7}

" Corner guards are sometimes necessary to solve the fortress problem and always sufficient" ${\ displaystyle {\ bigl \ lceil} {\ tfrac {n} {2}} {\ bigr \ rceil}}$

- Joseph O'Rourke: Galleries need fewer mobile guards: A variation on Chvátal's theorem . In: Geometriae Dedicata . 14, No. 3, 1983, pp. 273-283. doi : 10.1007 / BF00146907 .

An example of the need is any convex polygon. That this is sufficient follows from the following construction: For a general polygon consider the convex hull. Now triangulate the part of the plane that lies inside the convex hull but outside the polygon. Choose an artificial knot and connect all points of the convex hull to it. The polygon is now "opened" at any node of the convex hull: it is replaced by nodes and with incidences that are identical to, except for one edge that connects them to their neighbor on the convex hull . The resulting graph with nodes is a triangulation graph , i.e. three-colorable . One then calculates elementarily that a minimal chromatic class that does not contain is at most of the order . Argawall carried out the transfer of the proof to the orthogonal case and he comes to the conclusion that corner guards are always sufficient and sometimes necessary. Both proofs provide linear time algorithms for the construction of a corresponding guard set. ${\ displaystyle v _ {\ infty}}$ ${\ displaystyle x}$ ${\ displaystyle x}$ ${\ displaystyle x '}$ ${\ displaystyle x ''}$ ${\ displaystyle x}$ ${\ displaystyle n + 2}$ ${\ displaystyle v _ {\ infty}}$ ${\ displaystyle {\ bigl \ lceil} {\ tfrac {n} {2}} {\ bigr \ rceil}}$ ${\ displaystyle {\ bigl \ lceil} {\ tfrac {n} {4}} {\ bigr \ rceil} +1}$

For here you need free guards.

{\ displaystyle n = 13}

{\ displaystyle 5}

If you remove the restriction that guards can only be placed in the corners, you can show that this is always sufficient and sometimes necessary. As proof, an idea by Shermer has proven to be reasonable. A triangulation graph is constructed: Two additional points are chosen sufficiently far away to the right and left of the polygon. The convex hull can then be used to explain a graph with nodes for which a triangulation exists. In the event that the number of nodes on the convex hull is even, this graph can then be 3-colored, the additional nodes get the color one, the points on the hull then alternate with two and three. If it is odd, you can use a trick to add another knot and it is even. A smallest chromatic class then contains nodes. ${\ displaystyle {\ bigl \ lceil} {\ tfrac {n} {3}} {\ bigr \ rceil}}$ ${\ displaystyle n + 2}$ ${\ displaystyle \ left \ lfloor {\ tfrac {n + 2} {3}} \ right \ rfloor = \ left \ lceil {\ tfrac {n} {3}} \ right \ rceil}$

Overview of the results of the guard theory

sighted area	Polygon structure	Holes	Guard type	lower bound	upper bound	discussion
Inside	general		Corners	${\ displaystyle \ lfloor {\ frac {n} {3}} \ rfloor}$		here
				${\ displaystyle r}$		Lower bound here , upper bound almost trivial
		${\ displaystyle h}$		${\ displaystyle \ lfloor {\ frac {n + h} {3}} \ rfloor}$	${\ displaystyle \ lfloor {\ frac {n + 2h} {3}} \ rfloor}$	Lower for little ones here . Upper in O'Rourke p. 125 ff. ${\ displaystyle h}$
			edge	${\ displaystyle \ lfloor {\ frac {n + 1} {4}} \ rfloor}$	${\ displaystyle \ lfloor {\ frac {n} {3}} \ rfloor}$
	star-shaped		Corners	${\ displaystyle \ lfloor {\ frac {n} {3}} \ rfloor}$		Some lower bounds here . Upper bounds and rest in O'Rourke p. 116 ff.
				${\ displaystyle \ lfloor {\ frac {r} {2}} \ rfloor +1}$
			line	${\ displaystyle 1}$
			Dialgonal	${\ displaystyle 2}$
			edge	${\ displaystyle \ lfloor {\ frac {n} {5}} \ rfloor}$	${\ displaystyle \ lfloor {\ frac {n} {3}} \ rfloor}$
				${\ displaystyle \ lfloor {\ frac {r} {2}} \ rfloor +1}$
	orthogonal		Corners	${\ displaystyle \ lfloor {\ frac {n} {4}} \ rfloor = \ lfloor {\ frac {r} {2}} \ rfloor +1}$		here
		${\ displaystyle 1}$		${\ displaystyle \ lfloor {\ frac {n} {4}} \ rfloor}$		Analogous to the general case with holes O'Rourke p. 140 ff.
		${\ displaystyle 2}$	Point	${\ displaystyle \ lfloor {\ frac {n} {4}} \ rfloor}$
		${\ displaystyle h}$	Corners	${\ displaystyle \ lfloor {\ frac {n} {4}} \ rfloor}$	${\ displaystyle \ lfloor {\ frac {n + 2h} {4}} \ rfloor}$
			Diagonal	${\ displaystyle \ lfloor {\ frac {3n + 4} {16}} \ rfloor}$		O'Rourke p. 108 ff. After Aggarwal .
Outside	general		Corners	${\ displaystyle \ lceil {\ frac {n} {2}} \ rceil}$		here
			punk	${\ displaystyle \ lceil {\ frac {n} {3}} \ rceil}$
	orthogonal		Corners	${\ displaystyle \ lceil {\ frac {n} {4}} \ rceil +1}$		here
Inside and outside	general		Corners	${\ displaystyle \ lceil {\ frac {n} {2}} \ rceil}$		Füredi-Keitmann
	convex			${\ displaystyle \ lfloor {\ frac {n} {2}} \ rfloor}$		Füredi-Keitmann
	orthogonal			${\ displaystyle \ lceil {\ frac {n} {4}} \ rceil +1}$	${\ displaystyle \ lfloor {\ frac {5n} {12}} \ rfloor +2}$	Hoffmann-Kriegel
Legend ${\ displaystyle n}$ notes the number of corners. (Corners of holes are counted, if any) ${\ displaystyle h}$ notes the number of holes, if any. No entry means . ${\ displaystyle h = 0}$ ${\ displaystyle r}$ notes the number of concave corners. A corner is called concave, iff its interior angle is greater than is. ${\ displaystyle \ pi = 180 ^ {\ circ}}$ ${\ displaystyle \ lfloor \ dots \ rfloor}$ and are the Gaussian and Entier brackets . They round the enclosed expression up or down to an integer. ${\ displaystyle \ lceil \ dots \ rceil}$

More critical examples

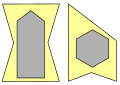
For star-shaped polygons
Proof of the lower bound in the number of corners for star-shaped polygons: Corner guards are needed here for corners . (One for each "spike." No corner guards 2 spikes or more.) ${\ displaystyle n = 24}$ ${\ displaystyle 8}$
Proof of the lower bound in the number of concave corners for star-shaped polygons: For every two points you need a guard at their concave corners. No corner more than two points.
Idea of proof of the lower bound in the number of corners for star-shaped polygons: Edge guards are needed for here . When generalizing for larger ones, the points must be selected to be so pointed that the rays induced by each point intersect a different edge of the “circle” for each point. ${\ displaystyle n = 25}$ ${\ displaystyle 5}$ ${\ displaystyle n}$
Example of a star-shaped polygon that requires two diagonal guards. Two of the four possible diagonals are shown: None intersects the core region highlighted in gray. This example was discovered by Shermer and Suri.

Boundaries in the number of concave corners and polygons with holes.

There are polygon classes that require a guard for each concave corner.

Guardians are required for corners . The left polygon goes back to Julian Sidarto. The two right on Tomas Shermer . ${\ displaystyle n = 8}$ ${\ displaystyle 3}$

Here you need guardians for corners. The left goes back to Shermer; the right to Arthur Delcher. This and the previous examples with holes were found on an O'Rourke seminar homework assignment. ${\ displaystyle 4}$ ${\ displaystyle n = 11}$

${\ displaystyle n = 24}$ and three holes need corner guards. ${\ displaystyle 9}$

literature

J. O'Rourke: Art gallery theorems and algorithms . Oxford University Press Oxford, 1987 ( PDF, online ).
A. Aggarwal: The art gallery theorem: its variations, applications and algorithmic aspects . 1984.
J. Urrutia: Art gallery and illumination problems . In: Handbook of computational geometry . 2000, pp. 973-1027.
Zoltán Füredi, DJ Kleitman: The prison yard problem . In: Combinatorica . 14, No. 3, 1994, pp. 287-300. doi : 10.1007 / BF01212977 .
Frank Hoffmann, Klaus Kriegel: Algorithms and Computation . 1993, A graph coloring result and its consequences for some guarding problems, p. 78-87 , doi : 10.1007 / 3-540-57568-5_237 .

Footnotes

Remarks

↑ Affiliation was proven under the condition . Many mathematicians assume this, but the proof has proven genuinely difficult in recent decades. (See P-NP problem ) ${\ displaystyle {\ mathcal {P}} \ neq {\ mathcal {NP}}}$

↑ The symbols are the Gaussian brackets . They round off the enclosed expression. Example: ${\ displaystyle \ lfloor \ dots \ rfloor}$ ${\ displaystyle \ lfloor {\ frac {11} {3}} \ rfloor = \ lfloor \ pi \ rfloor = 3}$

↑ For the notation see Landau symbol ${\ displaystyle {\ mathcal {O}} ()}$
↑ Other terms used for this are rectilinear , isothetic and rectanguloid .
↑ O'Rourke uses the term quadrilateralization .
↑ To model overlaps, one examines polygons as orthogonal, closed Jordan curves on a Riemann surface .
↑ For every orthogonal polygon, one can find a polygon that is "arbitrarily close" with too identical quadrilateration, the corners of which have pairs of different coordinates. ${\ displaystyle G}$ ${\ displaystyle G '}$ ${\ displaystyle G}$

Individual evidence

^ NJ Nilsson: A mobile automaton: An application of artificial intelligence techniques . Storming Media, 1969.
↑ LS Davis, ML Benedikt: Computational models of space: Isovists and isovist fields . 1979.
^ R. Honsberger: Mathematical Gems II: The Dolciani Mathematical Expositions . In: Mathematical Association of America . 84, 1976.
↑ ^a ^b V. Chvatal: A combinatorial theorem in plane geometry . In: J. Combin. Theory Ser. B . 18, No. 39-41, 1975, p. 32.
^ S. Fisk: A short proof of Chvátals watchman theorem . In: J. Combin. Theory Ser. B . 24, No. 3, 1978, p. 374.
↑ for the existence proofs of triangulations and coloring can be O'Rourke (1987) study
↑ D. Avis, GT Toussaint: An efficient algorithm for decomposing a polygon into star-shaped polygons . (pdf) In: Pattern Recognition . 13, No. 6, 1981, pp. 395-398.
^ O'Rourke : p. 31
^ J. Kahn, M. Klawe, D. Kleitman: Traditional galleries require fewer watchmen . In: SIAM Journal on Algebraic and Discrete Methods . 4, 1983, p. 194. doi : 10.1137 / 0604020 .
↑ Jörg-Rüdiger Wolfgang Sack: Rectilinear computational geometry. ACM, 1984, accessed March 11, 2010 . and JR Sack, G. Toussaint: A linear-time algorithm for decomposing rectilinear star-shaped polygons into convex quadrilaterals . In: Proceedings 19th Conference on Communications, Control, and Computing . 1981, p. 21-30 .
↑ Anna Lubiw: Decomposing polygonal regions into convex quadrilaterals . In: Proceedings of the first annual symposium on Computational geometry . ACM, Baltimore, Maryland, United States 1985, ISBN 0-89791-163-6 , pp. 97-106 , doi : 10.1145 / 323233.323247 ( online [accessed March 13, 2010]).
↑ cf. O'Rourke p. 152 ff.
^ O'Rourke : p. 267
↑ B. M Chazelle: Computational geometry and convexity . New Haven Yale Univ. 1980.

[3] Affiliation was proven under the condition . Many mathematicians assume this, but the proof has proven genuinely difficult in recent decades. (See P-NP problem ) ${\ displaystyle {\ mathcal {P}} \ neq {\ mathcal {NP}}}$

[6] The symbols are the Gaussian brackets . They round off the enclosed expression. Example: ${\ displaystyle \ lfloor \ dots \ rfloor}$ ${\ displaystyle \ lfloor {\ frac {11} {3}} \ rfloor = \ lfloor \ pi \ rfloor = 3}$

[10] For the notation see Landau symbol ${\ displaystyle {\ mathcal {O}} ()}$

[11] Other terms used for this are rectilinear , isothetic and rectanguloid .

[14] O'Rourke uses the term quadrilateralization .

[15] To model overlaps, one examines polygons as orthogonal, closed Jordan curves on a Riemann surface .

[16] For every orthogonal polygon, one can find a polygon that is "arbitrarily close" with too identical quadrilateration, the corners of which have pairs of different coordinates. ${\ displaystyle G}$ ${\ displaystyle G '}$ ${\ displaystyle G}$

[1] NJ Nilsson: A mobile automaton: An application of artificial intelligence techniques . Storming Media, 1969.

[2] LS Davis, ML Benedikt: Computational models of space: Isovists and isovist fields . 1979.

[4] R. Honsberger: Mathematical Gems II: The Dolciani Mathematical Expositions . In: Mathematical Association of America . 84, 1976.

[chvátal-5] V. Chvatal: A combinatorial theorem in plane geometry . In: J. Combin. Theory Ser. B . 18, No. 39-41, 1975, p. 32.

[7] S. Fisk: A short proof of Chvátals watchman theorem . In: J. Combin. Theory Ser. B . 24, No. 3, 1978, p. 374.

[8] r the existence proofs of triangulations and coloring can be O'Rourke (1987) study

[9] D. Avis, GT Toussaint: An efficient algorithm for decomposing a polygon into star-shaped polygons . (pdf) In: Pattern Recognition . 13, No. 6, 1981, pp. 395-398.

[12] O'Rourke : p. 31

[13] J. Kahn, M. Klawe, D. Kleitman: Traditional galleries require fewer watchmen . In: SIAM Journal on Algebraic and Discrete Methods . 4, 1983, p. 194. doi : 10.1137 / 0604020 .

[17] Jörg-Rüdiger Wolfgang Sack: Rectilinear computational geometry. ACM, 1984, accessed March 11, 2010 . and JR Sack, G. Toussaint: A linear-time algorithm for decomposing rectilinear star-shaped polygons into convex quadrilaterals . In: Proceedings 19th Conference on Communications, Control, and Computing . 1981, p. 21-30 .

[18] Anna Lubiw: Decomposing polygonal regions into convex quadrilaterals . In: Proceedings of the first annual symposium on Computational geometry . ACM, Baltimore, Maryland, United States 1985, ISBN 0-89791-163-6 , pp. 97-106 , doi : 10.1145 / 323233.323247 ( online [accessed March 13, 2010]).

[19] . O'Rourke p. 152 ff.

[20] O'Rourke : p. 267

[21] B. M Chazelle: Computational geometry and convexity . New Haven Yale Univ. 1980.