Quantum circuit

With quantum circuit is in the quantum computer science an abstract model for quantum computer called. The calculation that takes place in this is a sequence of quantum gates that carry out reversible transformations on the quantum mechanical counterpart of an n - bit register . This register is called the n - qubit here .

Reversible logic gates

In the classic computer, the logic gates with more than one input (all except the non-gate ) and one output are not reversible . For example, for an AND gate, it is not possible to deduce from output bit 0 whether the input values ​​were 0.1 or 1.0 or 0.0. However, it is theoretically possible in a classic computer to construct reversible gates for input values ​​of any length. A reversible gate is a reversible function, the n bit to n mapping bit, where the n -bit Date a character string of length n with the bits x ₁ , x ₂ , ..., x _n .

The n -bit date is an element of the set {0,1} ⁿ . This contains 2 ⁿ elements.

A reversible n -bit gate is a bijective mapping f from the set {0,1} ⁿ of n -bit data onto itself.

An example of such a gate f is a mapping which negates the first bit.

For practical reasons, only gates for small values ​​of n are considered here, i.e. n  = 1, n  = 2 or n  = 3. These gates can easily be described as tables. An example n  = 2 is the controlled no-gate , the Toffoli-gate and the Fredkin-gate .

For the consideration of quantum gates one has to define the quantum mechanical replacement of an n -bit datum.

The quantized version of a classical n -bit state space {0,1} ⁿ is

${\displaystyle H_{\operatorname {QB} (n)}=\ell ^{2}(\{0,1\}^{n}).}$

By definition, this is the space of complex-valued functions of {0,1} ⁿ and is a Prehilbert space . This space can also be viewed as an overlay of classic bit strings. Note that H _{QB ( n ) is} a vector space over the complex numbers of dimension 2 ⁿ .

The elements of this space are called n - qubits .

If x ₁ , x ₂ ,…, x _{n describes} the classic bit string in Bra-Ket notation, then is

${\displaystyle |x_{1},x_{2},\cdots ,x_{n}\rangle \quad }$

a specific n - qubit corresponding to the function that maps the classical bit string to 1 and all other strings to 0. These 2 ⁿ particular n -Qubits are the calculation state basis of the function. All n qubits are complex linear combinations of this basis.

A special kind of reversible function is required for a quantum gate, namely a unitary mapping . This is a mapping to H _{QB ( n )} in which the scalar products are preserved.

A reversible n -qubit quantum gate is a unitary mapping U from the space H _{QB ( n )} onto itself.

Again, only the unitary map U for small n is of interest. From a reversible n -bit gate f can be a reversible n -bit quantum gates W _f form, which is defined as follows:

${\displaystyle W_{f}(|x_{1},x_{2},\cdots ,x_{n}\rangle )=|f(x_{1},x_{2},\cdots ,x_{n})\rangle .}$

Note that W _f the calculation state based permuted .

Of particular interest is the 2-qubit CNOT gate W _CNOT . With this gate it becomes clear that there are many more quantum gates beyond the permutation of the basis. For example, a shift of the phase by multiplication with the following unitary matrix is ​​also permissible:

${\displaystyle U_{\theta }={\begin{bmatrix}e^{i\theta }&0\\0&1\end{bmatrix}},}$

so

${\displaystyle U_{\theta }|0\rangle =e^{i\theta }|0\rangle \quad U_{\theta }|1\rangle =|1\rangle .}$

Reversible circuits

→ Main article : Reversible computing

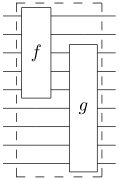
Again we first consider the reversible classical calculation. Basically there is no difference between a reversible n -bit circuit and a reversible n -bit gate. It is just a reversible function in the space of n -bit data. As already described in the previous section, for practical reasons one would like to have a small number of reversible gates that can be put together to form a reversible circuit. The assembly of a circuit is shown in the following example. Assume one has a reversible n -bit gate f and a reversible m -bit gate g . Assembling means making a new circuit by connecting a subset of the k  <  n of the outputs of f to a subset k of the inputs of g , as shown in the picture below. In this picture n  = 5, k  = 3 and m  = 7. The resulting circuit is also reversible and processes n  +  m  -  k bits.

In the following, this scheme is referred to as the classic network . When assembling these reversible machines, it is important that the intermediate stages are also reversible. This condition ensures that the entropy does not increase (decrease) within the machine. With this it is possible to show that the Toffoli gate is a quantum gate . This means that for any reversible classic n -bit circuit h , a classic combination of Toffoli gates can be generated in the manner described above, an n + m -bit circuit f , so that applies.

${\displaystyle f(x_{1},\ldots ,x_{n},\underbrace {0,\dots ,0} )=(y_{1},\ldots ,y_{n},\underbrace {0,\ldots ,0} )}$

The areas above the angle brackets are m 0 inputs and it applies

${\displaystyle (y_{1},\ldots ,y_{n})=h(x_{1},\ldots ,x_{n})}$.

Note that the end result always contains a string of m zeros as auxiliary bits. No waste is produced at any point, so that the calculation does not actually generate any entropy in the physical sense. From this it follows immediately that every function f (whether bijective or not) can be simulated by a circuit of Toffoli gates. However, if the imaging is not injective , the simulation must produce waste somewhere, e.g. B. the last step.

A similar connection of qubit gates can be defined for quantum circuits. This can be associated with the classic combination above by using an n qubit gate U instead of f and the m qubit gate W instead of g . A reversible quantum circuit is obtained from this, as shown in the following figure.

It can easily be shown that connecting the gates creates a unitary mapping on the n + m - k qubit space. It should also be noted that in real quantum computers the physical connection between the gates is one of the main problems, as it is one of the places where decoherence can occur.

In addition, some sets of well-known gates form universal gates . The above-mentioned single qubit phase gate U _{Θ is} universal for meaningful values ​​of Θ together with the 2-qubit CNOT gate W _CNOT . However, the universality is somewhat weaker in the case of quantum computation. Every reversible n -qubit circuit can be approximated as closely as desired by these two elementary gates . Note that there are uncountably many possible single qubit phase gates (one for each possible angle Θ). This means that an uncountable number of these gates cannot be made by finite circuits from { U _? , W _CNOT }.

Quantum calculations

Since many important numerical problems can be reduced to the computation of a unitary transformation U on a finite-dimensional space (the most prominent example is the discrete Fourier transformation ), one might expect that a quantum circuit for the transformation U can be built. In principle, one only has to prepare an n qubit state Ψ as the associated superposition of the calculation state basis for the input and then measure the outputs of UΨ. Unfortunately, there are two problems with this:

• One cannot measure the phase of messen for every base state. Hence there is no way to measure the full result. This is in the nature of quantum mechanical measurement .
• It is not possible to prepare the input state Ψ efficiently.

Nevertheless, quantum circuits for the discrete Fourier transform can be used as an intermediate step in other quantum circuits. However, it is a little more complicated to use. In fact, quantum computations are probabilistic .

A mathematical model for the simulation of probabilistic instead of classic calculations is now being created. Consider an r qubit circuit U with the register space H _{QB ( r )} . So U is a unitary map

${\displaystyle H_{\operatorname {QB} (r)}\rightarrow H_{\operatorname {QB} (r)}.}$

In order to associate this circuit with the classical mapping of bit strings, one specifies

• An input register X = {0.1} ^m of m (classical) bits.
• An output register Y = {0,1} ⁿ of n (classical) bits.

The content x = x ₁ ,…, x _{m of} the classic input register is somehow used for the initialization of the qubit register. Ideally this is done with the calculation state base.

${\displaystyle |{\vec {x}},0\rangle =|x_{1},x_{2},\cdots ,x_{m},\underbrace {0,\dots ,0} \rangle }$

There are 0 inputs under the brackets r  -  m .

Still, the perfect initialization is absolutely unrealistic. Assume, therefore, that the initialization is a blending state given by the density operator S. In a suitable metric, this is very similar to the ideal input state, e.g. B.

${\displaystyle \operatorname {Tr} \left({\big |}|{\vec {x}},0\rangle \langle {\vec {x}},0|-S{\big |}\right)\leq \delta }$

Similarly, the output register space communicates with the qubit register on by a Y approximate Observable A in relationship. It should be noted that observables in quantum mechanics are usually expressed in terms of projected magnitudes . If the variable is discrete, then the projected magnitude value is reduced to a family {E _λ }. Here λ is a parameter over a countable set. Similarly, an observable Y with a family of paired orthogonal projections E { _y indexed} by Y are associated. So is

${\displaystyle I=\sum _{y\in Y}\operatorname {E} _{y}.}$

A probability measure for Y corresponds to a given mixed state S

${\displaystyle \operatorname {Pr} \{y\}=\operatorname {Tr} (S\operatorname {E} _{y})}$

The function F : X → Y is calculated by the circuit U : H _{QB ( r )} → H _{QB ( r )} within ε if and only if all bit strings x of length m apply

${\displaystyle \left\langle {\vec {x}},0{\big |}U^{*}\operatorname {E} _{F(x)}U{\big |}{\vec {x}},0\right\rangle =\left\langle \operatorname {E} _{F(x)}U(|{\vec {x}},0\rangle ){\big |}U(|{\vec {x}},0\rangle )\right\rangle \geq 1-\epsilon }$

This applies

${\displaystyle \left|\operatorname {Tr} (SU^{*}\operatorname {E} _{F(x)}U)-\left\langle {\vec {x}},0{\big |}U^{*}\operatorname {E} _{F(x)}U{\big |}{\vec {x}},0\right\rangle \right|\leq \operatorname {Tr} ({\big |}|{\vec {x}},0\rangle \langle {\vec {x}},0|-S{\big |})\|U^{*}\operatorname {E} _{F(x)}U\|\leq \delta }$

so that

${\displaystyle \operatorname {Tr} (SU^{*}\operatorname {E} _{F(x)}U)\geq 1-\epsilon -\delta }$

Sentence . If so , then the probability distribution can ${\displaystyle \epsilon +\delta <{\frac {1}{2}}}$

${\displaystyle \operatorname {Pr} \{y\}=\operatorname {Tr} (SU^{*}\operatorname {E} _{y}U)}$

on Y can be used to determine F ( x ) with a sufficiently large number of samples with an arbitrarily small error probability. If one takes k independent samples from the probability distribution Pr on Y , then the probability that the value F ( x ) is measured more than k / 2 times is at least

${\displaystyle 1-e^{-2\gamma ^{2}k}}$

whereby . This follows from the Chernoff inequality . ${\displaystyle \gamma ={\frac {1}{2}}-\epsilon -\delta }$

See also

• Quantum gate
• List of quantum gates

literature

• Eli Biham, Gilles Brassard, Dan Kenigsberg, Tal Mor: Quantum computing without entanglement . In: Theoretical Computer Science . tape 320 , no. 1 , 2004, p. 15-33 , doi : 10.1016 / j.tcs.2004.03.041 , arxiv : quant-ph / 0306182 .
• MH Freedman, A. Kitaev, MJ Larsen, Z. Wang: Topological quantum computation . In: Bulletin of the AMS . tape 40 , no. 1 , 2003, p. 31-38 ( PDF ).
• Mika Hirvensalo: Quantum Computing . Springer, Berlin 2000, ISBN 3-540-66783-0 .
• Michael A. Nielsen, Isaac L. Chuang: Quantum Computation and Quantum Information . Cambridge University Press, 2000, ISBN 0-521-63503-9 .

Web links

• Quantum circuit on arxiv.org (English)
• Q-circuit is a macro library for drawing quantum circuits in LaTeX.

Individual evidence

1. ↑ A Yu Kitaev: Quantum computations: algorithms and error correction Quantum computations: algorithms and error correction . In: Russian Mathematical Surveys . tape 52 , 1997, pp. 1191-1249 , doi : 10.1070 / RM1997v052n06ABEH002155 .