Retraction and coretraction
In category theory , a retraction is understood to mean a morphism that has a right inverse, that is, to which there is a morphism with . The dual concept of a retraction is that of coretraction (or cut ), i.e. a morphism that has a left inverse. The right inverse of a retraction is a coretraction and vice versa.
An object of a category is called a retract of an object if there is a morphism and a retraction to , i.e. a morphism with .
Every retraction is an extreme and even regular epimorphism . Likewise, every coretraction is extreme and even regular monomorphism and even difference kernel .
Special categories
Topological spaces
The term retraction is used in algebraic topology . In the category of topological spaces, all extreme monomorphisms and thus all coretractions are topological embeddings . In the case of topological spaces, this enables a different perspective and definition: A retraction is a continuous left inverse of a topological embedding. Or to put it concretely: a retraction is a continuous mapping of a topological space in itself, so that every element of the image set is a fixed point .
This also allows a concrete definition of the retract: A subspace of a topological space is called a retract of if there is a retraction for embedding .
is retract of if and only if every continuous mapping can be continued continuously to a mapping :
- If there is a retraction , there is a continuous continuation .
- A continuation from to a continuous mapping is a retraction.
In a Hausdorff area , every retract is closed: Be a retract with retraction . Now consider a converged network on . The image network converges towards (since it is continuous) and is equal to the original network. Since the limit value of a network in Hausdorff areas is unambiguous, it applies and is complete. In non-Hausdorff areas this does not apply: In non- T₁ areas there are non-closed single-element sets, which are obviously retracts. As an example of T₁ room with non-completed retract the look cofiniteness on : with and for a retraction, the picture is not complete.
Deformation retract
is called deformation retraction of if homotop is too relative .
Deformation retractions are special homotopy equivalences that produce this equivalence relation .
Examples
Elementary example
The following figure is an illustrative example of a retraction in the real numbers :
Brouwer's Fixed Point Theorem in the one-dimensional case
The Brouwer fixed-point theorem states that any continuous mapping of a solid sphere has a fixed point in itself. From a topological point of view, a one-dimensional full sphere corresponds to a closed interval, for example . If there were a continuous, fixed-point-free mapping , this would result in a retraction by means of (since the denominator would never disappear), i.e. H. should be retract from . Such a retraction cannot exist, however, since the relationship is preserved under continuous images.
Closed sub-rooms of the Baire room
In the Baire area, the following applies: For any closed sub-rooms (these are always Polish sub-rooms) there is a retract of . Note that Baire space is totally disconnected, and therefore the concept of context does not provide any restrictions for retracts.
Arrow category
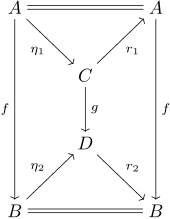
Let be a category, the corresponding arrow category is then the category of functors from the category with two objects and three morphisms into the category . These are called arrows and can be identified with the morphisms in . An arrow is a retract of an arrow if there is a natural transformation (i.e. a commuting square) and a retraction , so the following diagram commutes:
Set theory
In the category of all sets and the functions between them, a morphism (that is, a function between two sets) is a retraction if and only if it is surjective . This statement is equivalent to the axiom of choice in set theory . Accordingly, a morphism is a coretraction if and only if it is injective and there is a morphism in the opposite direction. However, this statement does not require the axiom of choice. From these statements it follows that in every concrete category the retractions must be surjective and the coretractions injective, which generally does not apply to general epi- or monomorphisms which correspond to the retractions or coretractions in the category of sets.
Individual evidence
- ↑ Dieter Pumplün : Elements of the category theory . 1st edition. Spektrum Akademischer Verlag , Heidelberg 1999, ISBN 3-86025-676-9 , p. 64 .
- ↑ extremal monomorphism , entry in the nLab . (English)
- ^ A b William Fulton : Algebraic Topology . 1st edition. Springer , New York 1995. Section 4b, ISBN 0-387-94327-7






























![f \ colon \ mathbb {R} \ to [0,1], x \ mapsto {\ begin {cases} 0 & {\ mbox {for}} x <0 \\ x & {\ mbox {for}} 0 \ leq x \ leq 1 \\ 1 & {\ mbox {for}} x> 1 \ end {cases}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c144bc26db630a8a73fca87da451de1c3485a3bf)
![\ left [-1.1 \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/79566f857ac1fcd0ef0f62226298a4ed15b796ad)
![f \ colon \ left [-1.1 \ right] \ to \ left [-1.1 \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/21bd4222baa0624dc746d3c3f698bca73e6e3ac6)
![g \ colon \ left [-1.1 \ right] \ to \ {- 1.1 \}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18f94363ff27106ecefc74ffcce8e70d62b0c664)