Traktrix

Tractrix ( v. Lat. Trahere "grind, drag"), even drag curve , pulling curve , tensile curve , Treidelkurve , is a special plane curve . The name is explained by the fact that this curve is described by a mass point that is pulled on a rod.

Actual tractrix, function graph for x and y, P starts in (4,0)

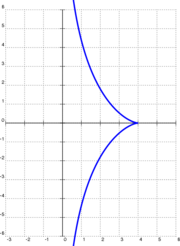
The actual (straight line) tractrix is ​​the curve in which the section between the contact point and the coordinate axis is constant for each tangent . It is also called the Huygens Traktrix , after Christiaan Huygens , who solved the underlying problem in 1693 after it was described by Claude Perrault . It is one of the curves known by the common name dog curve . This curve plays an important role in hyperbolic geometry .

Soon after, Leonhard Euler and others dealt with the general tractrix, which allows any guide curves. It plays an important role in the modeling of driving behavior, namely reversing and behavior when driving through a curve. The knowledge gained from this is used in the design of roads to check whether they are passable.

Actual Traktrix

Education Act

Let be the starting point of a “puller” and the starting point of a “pulled” as well as the distance . ${\displaystyle A_{0}}$ ${\displaystyle P_{0}}$ ${\displaystyle d}$ ${\displaystyle A_{0}P_{0}>0}$

If the point moves on a straight line and the point “follows” it at a constant distance , then a tractrix passes through . ${\displaystyle A}$ ${\displaystyle P}$ ${\displaystyle d}$ ${\displaystyle P}$

Function equation in Cartesian coordinates

${\displaystyle A_{0}(0|0)}$at the origin , on the x-axis , moves along the y-axis : ${\displaystyle P_{0}(d|0)}$ ${\displaystyle A}$

${\displaystyle y(x)=\pm \ d\cdot \underbrace {\ln \left|{d+{\sqrt {d^{2}-x^{2}}} \over x}\right|} _{=\operatorname {arcosh} {\frac {d}{x}}}\mp {\sqrt {d^{2}-x^{2}}}}$

An explicit representation according to x (y) is not possible here.

Parametric representations

• with results in an elegant shape (with six ): ${\displaystyle t=arcosh{\frac {d}{y}}}$ ${\displaystyle z={\frac {1}{\cosh z}}}$

${\displaystyle x(t)=\pm \ d\cdot (t-\tanh t);}$   ${\displaystyle \quad y(t)=d\cdot \operatorname {sech} t}$

• with , the angle between the x-axis and the tangent - does not require a hyperbolic function : ${\displaystyle \omega ,\sin \omega ={\frac {y}{d}},0\leq \omega \leq {\frac {\pi }{2}}}$

${\displaystyle x(\omega )=\pm \ d\cdot \left(\cos \omega +\ln \tan {\omega \over 2}\right);}$   ${\displaystyle y(\omega )=d\cdot \sin \omega }$

• with , a representation that makes it easier to work with tabulated values : ${\displaystyle \lambda =\tan {\frac {\omega }{2}}}$

${\displaystyle x(\lambda )=\pm \ d\cdot \left({{\lambda ^{2}-1} \over {\lambda ^{2}+1}}-\ln \lambda \right);}$   ${\displaystyle y(\lambda )=2d\cdot {{\lambda } \over {\lambda ^{2}+1}}}$

Derivation

In the following the curve is considered in the 1st main position: moves along the x-axis, with : ${\displaystyle A_{0}(0|0),P_{0}(0|d),A}$ ${\displaystyle a=AA_{0}}$

1. The following differential equation ( tangent condition ) can be read directly from the law of formation with : ${\displaystyle d^{2}=(a-x)^{2}+y^{2}}$

   ${\displaystyle y'={\mathrm {d} y \over \mathrm {d} x}=\mp \ {y \over {a-x}}=\mp \ {y \over {\sqrt {d^{2}-y^{2}}}}}$

2. The solution succeeds with substitution . This corresponds to the above-mentioned parameters representation: . ${\displaystyle {\frac {d}{y}}=\cosh t}$ ${\displaystyle y={\frac {d}{\cosh t}}}$
3. It follows and then by separating the variables ${\displaystyle dy=-d\cdot {\frac {\sinh t}{\cosh ^{2}t}}dt}$ ${\displaystyle {\mathrm {d} }x\,=\,\mp \,{\frac {\sqrt {d^{2}-y^{2}}}{y}}\,{\mathrm {d} }y\,=\,\pm \,d\,\left(1-{\frac {1}{\operatorname {cosh} ^{2}t}}\right)\,{\mathrm {d} }t}$

Integration delivers and back substitution: ${\displaystyle x=\pm d\cdot (t-\tanh t)}$
${\displaystyle 4.\quad x(y)=\pm \ d\,\left(\operatorname {arcosh} {d \over y}-{\sqrt {1-\left({y \over d}\right)^{2}}}\right)}$

properties

• Obvious is . Is is the graph mirror image to the y-axis. ${\displaystyle 0<|y|\leq |d|}$ ${\displaystyle d<0}$
• For both possible tangents coincide with the y-axis , so the point is actually a point . ${\displaystyle P_{0}(0|d)}$ ${\displaystyle P_{0}}$
• The length of the curve between and is calculated as: ${\displaystyle x=x_{1}}$ ${\displaystyle x=x_{2}}$ ${\displaystyle l=d\cdot \ln \left({y_{1} \over y_{2}}\right)}$
• The area under the Traktrix: ${\displaystyle A=d^{2}\cdot {\tfrac {\pi }{2}}}$
• The evolution of the Traktrix is ​​the catenoids ${\displaystyle x=d\cdot \operatorname {cosh} \left({y \over d}\right)}$
• If this curve is rotated around the x-axis, the pseudosphere is created , which takes on the role of the sphere in hyperbolic geometry . For example, the area under the tract is the same as that of the semicircle . As a geodesic, the tractrix is the equivalent of the straight line in "normal" (Euclidean) space.

General tractrix

The term Traktrix can be generalized:

Given a parameter t , a curve k (the leading curve ), any point A ₀ ( starting point ) that lies on the curve k , and any point P ₀ . Let d be the distance A ₀ P ₀ .

If the point A ( t ) with A (0) = A ₀ moves along the curve k with increasing t , the point P ( t ) "follows" it with P (0) = P ₀ at a constant distance d .

The set of all points that P ( t ) passes through is called the tractrix of curve k .

${\displaystyle \mathbf {A} (t)={\mathbf {P} (t)}+d\cdot {\frac {\mathbf {\dot {P}} (t)}{|{\mathbf {{\dot {P}}(t)} }|}}}$ With ${\displaystyle t:{\mathbf {\dot {P}} (t)}\neq 0}$

The Traktrix is ​​thus a general radiodrome with the function ${\displaystyle \xi (t)={\tfrac {d}{|{\mathbf {\dot {P}} (t)}|}}}$

Application in road construction

The white area represents the trailing curve of a car when driving on a roundabout .

With the help of the drag curve, the driving behavior of vehicles can be modeled, in particular the space required when cornering, but also the behavior when driving backwards and when towing a second vehicle.

When steering operation of a vehicle running axes behind the steering axle " off track ": follow not exactly the same path, so that passed over a larger area for cornering, as the track status dictates.

The size and type of the swept area depends on several factors:

• The driving behavior of the vehicle driver
• The design speed, i.e. H. the maximum driving speed for which the road is designed.
• The curve radius : the tighter a curve is driven, the wider the swept area.
• The length of the vehicle: the longer a vehicle is, the larger the swept area.
• The position of the axles: Depending on where the axles are in relation to the length of the vehicle, a larger area is covered either on the inside of the curve or on the outside of the curve (warning "rear shears").
• The structure of the vehicle: trailer , semi-trailer , trailer etc.
• The number of steered or rotatable axles.

The swept area can be determined with the help of prefabricated drag curves that have been created for specific measurement vehicles. For special vehicles, the towing curves can be calculated with the help of computer simulations . The so-called driving line forms the basis for every calculation . The vehicle is moved with its guide point (usually the center of the steering axis) along this line.

The swept areas are covered by traffic lights , signs and the like. Ä. To be kept free and to be attached accordingly. For this, for example, lane widening is necessary for narrow radii . Furthermore, when creating curves and crossings, care must be taken that oncoming traffic is not obstructed and endangered.

This driving geometry dimensioning of traffic systems is in contrast to the driving dynamics design, as it is used in particular on country roads and motorways.

Norms and standards

Germany

• FGSV-Verlag: Measurement vehicles and drag curves for checking the passability of traffic areas, 2001

Web links

Commons : Tractrix  - album with pictures, videos and audio files

• Tracking problems, menu: trailing curves - Java applets
• Johanneum Lüneburg Curves Traktrix ( Memento from June 9, 2007 in the Internet Archive ) - Article for students
• Tractrix - From MathWorld - (English) , further references.
• Lexicon of accident reconstruction
• Summary of software for calculating drag curves