Trägheitsmoment

Das Trägheitsmoment ist eine physikalische Größe, die die Trägheit eines Körpers bei Rotationsbewegungen beschreibt. Sie ist damit das Äquivalent zur (trägen) Masse der Translationsbewegungen.

Bedeutung

Die Bedeutung des Trägheitsmoments soll hier durch Vergleich zwischen einer geradlinigen Translationsbewegung (also der Bewegung entlang einer Geraden) und einer Drehbewegung erfolgen:

• Sollen beispielsweise ein Fahrrad und ein Eisenbahnwagen auf dieselbe Geschwindigkeit beschleunigen werden, so ist intuitiv klar, dass für dieselbe Beschleunigung der Eisenbahnwagen viel kräftiger angeschoben werden muss als das Fahrrad. Die Stärke der nötigen Kraft hängt mit der Masse zusammen.
• Für Rotationsbewegungen ist die Sache ein wenig komplizierter. Sollen zwei Kugeln gleicher Masse – eine aus Holz und eine aus Blei – zum Drehen gebracht werden, so könnte man annehmen, dass man wegen derselben Masse auch dasselbe Drehmoment (das Pendant zur Kraft) benötigte. Dies ist jedoch nicht der Fall, denn je weiter außen (d.h. von der Drehachse entfernt) die Masse sitzt, desto größer ist das benötigte Drehmoment, um beide Kugeln in eine gleichschnelle Drehung zu versetzen. Da die Holzkugel bei gleicher Masse jedoch viel größer ist, benötigt man auch ein größeres Drehmoment. Die Eigenschaft der beiden Kugeln, wie schwer sie in Drehung zu versetzen sind, nennt man Trägheitsmoment.

Mit einem einfachen Experiment kann man die Auswirkung auf die Drehgeschwindigkeit bei Änderung des Trägheitsmoments aber konstant gehaltener Masse selbst ausprobieren. Dazu setzt man sich einen Schreibtischstuhl, streckt Arme und Beine nach außen und versetzt sich dann in Drehung. Durch Anziehen von Armen und Beinen nimmt das Trägheitsmoment ab – mit der Folge, dass die Drehbewegung schneller wird. Erneutes Ausstrecken verlangsamt die Bewegung wieder. Um den Effekt zu verstärken kann man dabei einen schweren Gegenstand wie z. B. eine Hantel in jede Hand nehmen. Je größer dabei die Masse des Gegenstandes, desto stärker der Effekt.

Ein weiteres bekanntes Beispiel zu diesem Experiment ist ein Schlittschuhläufer bei einer Pirouette. Die Kontrolle der Drehgeschwindigkeit kann dabei allein aus der Verlagerung seiner Körpermasse bezüglich seiner Drehachse erfolgen. Sobald er z. B. die Arme einzieht, dreht er sich schneller – ein erneutes Schwungholen ist dazu nicht nötig. Da dieser Effekt insbesondere aus dem Eiskunstlauf bekannt ist, wird er auch als Pirouetteneffekt bezeichnet.

Siehe auch: Drehimpulserhaltung

Formelzeichen und Einheit

Für das Trägheitsmoment wird in der Literatur in der Regel ein $I$ oder ein $J$ verwendet. Diese Wahl leitet sich ab aus dem lateinischen Wort iners (untätig, träge). Sehr selten wird das Trägheitsmoment deshalb auch als Inertialmoment bezeichnet, wohingegen im Englischen die Bezeichnung moment of inertia üblich ist. In Literatur zur theoretischen Mechanik wird manchmal auch ein $\Theta$ (Großes Theta) benutzt, insbesondere im Zusammenhang mit dem Trägheitstensor. In diesem Artikel wird durchgehend $I$ für das Trägheitsmoment verwendet.

Die Einheit des Trägheitsmoment lässt sich unmittelbar aus der unten angegebenen Berechnung ablesen. Sie lautet $[I]=\mathrm {kg} \,\mathrm {m^{2}}$.

Berechnung

Das Trägheitsmoment $I$ ist immer in Bezug auf die jeweilige Drehachse zu sehen. Für eine konkrete Bestimmung gibt man sich eine Drehachse vor und verfährt nach einer der folgenden Methoden.

Masseverteilung

Besteht ein sich drehender Körper aus einzelnen Massenpunkten, so berechnet sich das Trägheitsmoment wie folgt:

$I=\sum _{i}m_{i}r_{i}^{2}$

Dabei ist $m_{i}$ die Masse und $r_{i}$ der Abstand von der Drehachse des $i$-ten Teilchens. Es werden also alle Massen im Produkt mit dem Quadrat des Abstandes von der Achse aufsummiert. Dreht sich ein Körper beispielsweise um die $x$-Achse, so lautet das zugehörige Trägheitsmoment:

$I_{x}=\sum _{i}m_{i}(y_{i}^{2}+z_{i}^{2})$

In der Realität kommen keine einzelnen Massenpunkte ohne Ausdehnung vor – ein Körper besteht in der Regel aus einer kontinuierlichen Massenverteilung. Für diesen Fall muss die Summe durch ein Integral über das Volumen $V$ des Körpers ersetzt werden:

$I=\int _{V}r^{2}\rho ({\vec {r}})\,\mathrm {d} V=\int r^{2}\,\mathrm {d} m$

Mit $\rho ({\vec {r}})$ ist die Dichte und mit $\mathrm {d} m$ das sogenannte Massenelement gemeint. Der zweite Ausdruck ist eine Kurzschreibweise, welche häufig in der Literatur zu finden ist. Das Integral von dm über den ganzen Körper entspricht dessen Masse $m$. Zur konkreten Berechnung wird das erste Integral benutzt.

Ist die Dichte des Körpers über das gesamte Volumen konstant, so vereinfacht sich die Berechnung zu

$I=\rho \int _{V}r^{2}\,\mathrm {d} V$

In diesem Fall spricht man auch von einer homogenen Masseverteilung. Dazu ist weiter unten eine Beispielrechnung angegeben.

Trägheitstensor

Der Trägheitstensor $\mathrm {\Theta }$ eines Körpers stellt gewissermaßen eine Verallgemeinerung des Trägheitsmomentes dar. Aus diesem lässt sich das Trägheitsmoment bezüglich einer beliebigen, durch den Schwerpunkt gehenden Achse berechnen. Wenn ein starrer Körper um eine solche Achse mit der Winkelgeschwindigkeit ${\vec {\omega }}$ rotiert, so lautet die Formel

$I={\frac {1}{\omega ^{2}}}\sum _{\alpha =1}^{3}\sum _{\beta =1}^{3}\Theta _{\alpha \beta }\omega _{\alpha }\omega _{\beta }$

oder in Matrixschreibweise

$I={\frac {1}{\omega ^{2}}}\,{\vec {\omega }}^{T}\cdot \mathrm {\Theta } \cdot {\vec {\omega }}$

Herleitung

Sei der rotierende Körper aus einzelnen Massepunkten aufgebaut. Für die Ortsvektoren ${\vec {r}}_{i}$ der Massepunkte soll ein kartesisches Koordinatensystem verwendet werden, dessen Ursprung mit dem Schwerpunkt des Körpers zusammenfällt. Sei ${\vec {r}}_{i}$ der Ortsvektor des $i$-ten Massepunktes und $s_{i}$ sein Abstand von der Drehachse, dann gilt

$s_{i}={\sqrt {({\vec {r}}_{i})^{2}-\left({\frac {\vec {\omega }}{\omega }}\cdot {\vec {r}}_{i}\right)^{2}}}$

und somit für das Trägheitsmoment

$I=\sum _{i}m_{i}s_{i}^{2}=\sum _{i}m_{i}\left(({\vec {r}}_{i})^{2}-\left({\frac {\vec {\omega }}{\omega }}\cdot {\vec {r}}_{i}\right)^{2}\right)={\frac {1}{\omega ^{2}}}\sum _{i}m_{i}\left(({\vec {\omega }})^{2}({\vec {r}}_{i})^{2}-\left({\vec {\omega }}\cdot {\vec {r}}_{i}\right)^{2}\right)$

$={\frac {1}{\omega ^{2}}}\sum _{\alpha ,\beta =1}^{3}\left\{\sum _{i}m_{i}\left(({\vec {r}}_{i})^{2}\delta _{\alpha \beta }-r_{i\alpha }r_{i\beta }\right)\right\}\omega _{\alpha }\omega _{\beta }={\frac {1}{\omega ^{2}}}\sum _{\alpha ,\beta =1}^{3}\Theta _{\alpha \beta }\omega _{\alpha }\omega _{\beta }$

mit dem Trägheitstensor

$\Theta _{\alpha \beta }=\sum _{i}m_{i}\left(({\vec {r}}_{i})^{2}\delta _{\alpha \beta }-r_{i\alpha }r_{i\beta }\right)$.

Die Steiner-Regel

Illustration der Steiner-Regel. Drehachse 1 geht durch den Schwerpunkt des Körpers der Masse m. Drehachse 2 ist um den Abstand d verschoben.

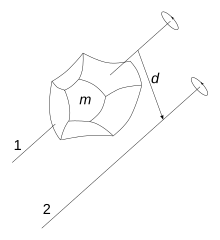
Ist das Trägheitsmoment $I_{\mathrm {S} }$ für eine Achse durch den Schwerpunkt eines Körpers bekannt, so kann mithilfe der Steiner-Regel das Trägheitsmoment $I$ für eine beliebige parallel verschobene Drehachse berechnet werden. Die Formel lautet:

$\left.I=I_{\mathrm {S} }+md^{2}\right.$

Dabei gibt $d$ den Abstand von alter zu neuer Drehachse an. Die Gültigkeit dieser Formel lässt sich direkt aus der Berechnung für eine Massenverteilung beweisen.

Man kann die Steiner-Regel für zwei beliebige parallele Drehachsen verallgemeinern. Dazu muss die Steiner-Regel zweimal hintereinander angewendet werden: Zunächst verschiebe man die Drehachse so, dass sie durch den Schwerpunkt des Körpers geht, danach auf den gewünschten Zielort.

$I_{\mathrm {neu} }=I_{\mathrm {alt} }+m(d_{\mathrm {neu} }^{2}-d_{\mathrm {alt} }^{2})$

Wenn der Trägheitstensor für einen Körper bekannt ist, so lassen sich mit diesem und der Steiner-Regel die Trägheitsmomente des Körpers für Rotationen um eine beliebige Drehachse im Raum berechnen.

Hauptträgheitsachsen

Betrachtet man einen unregelmäßig geformten Körper, der um eine Achse durch seinen Schwerpunkt rotiert, so variiert dessen Trägheitsmoment je nach Lage der Drehachse. Dabei gibt es zwei Achsen, bezüglich derer das Trägheitsmoment des Körpers maximal bzw. minimal ist. Diese Achsen stehen immer senkrecht zueinander und bilden zusammen mit einer dritten, wiederum senkrecht auf beiden stehenden Achse die Hauptträgheitsachsen des Körpers.

Die Hauptträgheitsachsen fallen mit eventuell vorhandenen Symmetrieachsen des Körpers zusammen. Sind zwei Hauptträgheitsmomente gleich groß, so sind alle Drehachsen in der Ebene, die von den zugehörigen Hauptträgheitsachsen aufgespannt wird, ebenfalls Hauptträgheitsachsen mit dem gleichen Trägheitsmoment. Das ist bei zylindersymmetrischen Körpern unmittelbar klar, gilt aber z. B. ebenso für einen Stab mit quadratischer oder hexagonaler Grundfläche. Für den Fall, dass alle Hauptträgheitsmomente identisch sind, ist jede Drehachse durch den Schwerpunkt eine Hauptträgheitsachse mit dem gleichen Trägheitsmoment. Für alle regelmäßigen Körper wie Kugel, Tetraeder, Würfel, usw. ist demnach das Trägheitsmoment für jede Achse durch den Schwerpunkt gleich groß.

Siehe auch: Trägheitsellipsoid

Beispiele

Trägheitsmomente von Himmelskörpern

Fast alle größeren Körper im Weltall (Sterne, Planeten) sind angenähert kugelförmig und rotieren mehr oder weniger schnell. Das Trägheitsmoment um die Rotationsachse ist immer das größte des Himmelskörpers.

Die Differenz dieses „polaren“ und des äquatorialen Trägheitmoments hängt mit der Abplattung des Körpers zusammen, also seiner Verformung der reinen Kugelgestalt durch die Fliehkraft der Rotation. Bei der Erde liegt diese Differenz bei 0,3 Prozent, entspricht also fast der Erdabplattung von 1:298,24. Beim rasch rotierenden Jupiter sind diese Relativwerte rund 20mal größer.

Das Trägheitsmoment eines Himmelskörpers lässt wegen r² im obigen Integral auf die innere Konzentration seiner Masse schließen. Jenes der Erde ist viel kleiner, als wenn sie homogen aufgebaut wäre. Daraus kann man errechnen, dass der Erdkern aus Eisen (oder metallisch verdichtetem Wasserstoff) besteht.

Trägheitsmomente einfacher geometrischer Körper

Vorlage:Highlight1 | Abbildung	Vorlage:Highlight1 | Beschreibung	Vorlage:Highlight1 | Trägheitsmoment
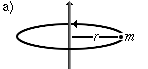
	Punktmasse im senkrechten Abstand $r$ um eine Drehachse.	$I=m\cdot r^{2}$
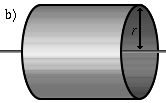
	Zylindermantel um seine Körperachse rotiert.	$I=m\cdot r^{2}$
	Vollzylinder um seine Körperachse rotiert.	$I={1 \over 2}m\cdot r^{2}$
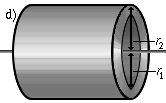
	Hohlzylinder um seine Körperachse rotiert. Das „+“ sieht zunächst verblüffend aus, doch die Masse ist nicht wie beim Vollzylinder homogen verteilt, sondern liegt nur noch im Außenbereich. Ein Hohlzylinder hat also, bei gleicher Masse, im Vergleich zum Vollzylinder ein größeres Massenträgheitsmoment.	$I={1 \over 2}m\cdot (r_{2}^{2}+r_{1}^{2})$
	Vollzylinder um den Schwerpunkt senkrecht zu seiner Körperachse rotiert.	$I={1 \over 4}m\cdot r^{2}+{1 \over 12}m\cdot l^{2}$
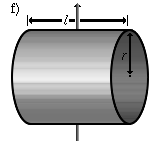
	Zylindermantel um den Schwerpunkt senkrecht zu seiner Körperachse rotiert.	$I={1 \over 2}m\cdot r^{2}+{1 \over 12}m\cdot l^{2}$
	Dünner Stab um den Schwerpunkt senkrecht zu seiner Körperachse rotiert. Diese Formel ist eine Näherung für einen Zylinder mit $r\ll l$.	$I={1 \over 12}m\cdot l^{2}$
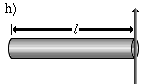
	Dünner Stab um sein Ende senkrecht zu seiner Körperachse rotiert. Diese Formel kann mit der Steiner-Regel aus Fall g) hergeleitet werden.	$I={1 \over 3}m\cdot l^{2}$
	Kugelschale um ihren Schwerpunkt rotiert.	$I={2 \over 3}m\cdot r^{2}$
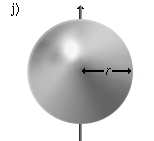
	Massive Kugel um ihren Schwerpunkt rotiert.	$I={2 \over 5}m\cdot r^{2}$
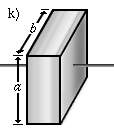
	Quader um seinen Schwerpunkt rotiert.	$I={1 \over 12}m\cdot (a^{2}+b^{2})$

Beispielrechnung: Trägheitsmoment der homogenen Vollkugel

Zum Verständnis von diesem Abschnitt sind grundlegende Kenntnisse der Integralrechnung und Koordinatentransformation hilfreich.

Um das Trägheitsmoment einer massiven homogenen Kugel bezüglich einer Drehachse durch den Kugelmittelpunkt zu berechnen, wird das im Abschnitt „Berechnung“ angegebene Integral verwendet. Der Einfachheit halber soll der Kugelmittelpunkt im Ursprung eines kartesischen Koordinatensystems liegen und die Drehachse entlang der $z$-Achse verlaufen. Um das Integral

$I=\rho \int _{V}(x^{2}+y^{2})\,\mathrm {d} V$

auszuwerten, empfiehlt es sich statt kartesischen lieber Kugelkoordinaten zu verwenden. Beim Übergang müssen dabei die kartesischen Koordinaten x,y,z und das Volumenelement dV durch die Kugelkoordinaten $r,\vartheta ,\varphi$ ausgedrückt werden. Das geschieht mithilfe der Ersetzungsregeln

$x=r\sin \vartheta \cos \varphi$

$y=r\sin \vartheta \sin \varphi$

$z=r\cos \vartheta$

und der Funktionaldeterminanten

$\mathrm {d} V=r^{2}\sin \vartheta \,\mathrm {d} r\,\mathrm {d} \vartheta \,\mathrm {d} \varphi .$

Einsetzen in den Ausdruck für das Trägheitsmoment liefert

$I=\rho \int _{0}^{R}\!\mathrm {d} r\,\int _{0}^{\pi }\!\mathrm {d} \vartheta \,\int _{0}^{2\pi }\!\mathrm {d} \varphi \,r^{4}\sin ^{3}\vartheta$

Hier zeigt sich der Vorteil der Kugelkoordinaten: Die Integralgrenzen hängen nicht voneinander ab. Die beiden Integrationen über r und $\varphi$ lassen sich daher elementar ausführen. Das verbleibende Integral in

$I={\frac {2}{5}}\pi \rho R^{5}\int _{0}^{\pi }\sin ^{3}\vartheta \,\mathrm {d} \vartheta$

kann durch partielle Integration mit

$u=\sin ^{2}\vartheta$

$v^{\prime }=\sin \vartheta$

gelöst werden:

$\int _{0}^{\pi }\sin ^{3}\vartheta \,\mathrm {d} \vartheta ={\frac {4}{3}}.$

Für das Trägheitsmoment ergibt sich schließlich:

$I={\frac {2}{5}}\cdot {\frac {4}{3}}\pi \rho R^{5}={\frac {2}{5}}\rho VR^{2}={\frac {2}{5}}MR^{2}$

Experimentelle Bestimmung

Zur Messung eines Trägheitsmoments eines Körpers verwendet man einen Drehtisch. Dieser besteht aus einer Kreisscheibe, die um ihre Symmetrieachse drehbar ist und einer Schneckenfeder. Sie bewirkt bei einer Drehung der Scheibe ein rücktreibendes Drehmoment $D$, das direkt proportional zum Auslenkwinkel $\phi$ ist: $D=-D_{r}\phi$. Die Proportionalitätskonstante $D_{r}$ nennt man Direktionsmoment oder Richtmoment. Ihr Wert hängt von der Stärke der Feder ab. Die Scheibe führt nun harmonische Schwingungen mit der Schwingungsdauer

$T_{0}=2\pi {\sqrt {\frac {I_{0}}{D_{r}}}}$,

aus, wobei $I_{0}$ das Trägheitsmoment der Scheibe ist. Legt man nun zusätzlich einen Körper mit bekanntem Trägheitsmoment $I_{1}$ auf die Scheibe, so ändert sich die Schwingungsdauer zu

$T_{1}=2\pi {\sqrt {\frac {I_{0}+I_{1}}{D_{r}}}}$.

Aus der Differenz

$T_{1}^{2}-T_{0}^{2}=4\pi ^{2}{\frac {I_{1}}{D_{r}}}$

lässt sich das Direktionsmoment $D_{r}$ des Drehtisches bestimmen und aus obiger Formel für $T_{0}$ erhält man dann das Trägheitsmoment $I_{0}$ des Drehtisches. Legt man nun einen beliebigen Körper auf den Drehtisch, so kann man sein Trägheitsmoment $I$ bezüglich der Rotationsachse aus der gemessenen Schwingungsdauer

$T=2\pi {\sqrt {\frac {I_{0}+I}{D_{r}}}}$

berechnen.

Siehe auch

• Flächenträgheitsmoment
• Kreisel

Literatur

• Paul A. Tipler: Physik. 3. korrigierter Nachdruck der 1. Auflage 1994, Spektrum Akademischer Verlag Heidelberg Berlin, 2000, ISBN 3-86025-122-8
• Ernst W. Otten: Repetitorium Experimentalphysik. Springer-Verlag Berlin Heidelberg, 1998, ISBN 3-540-62987-4
• Torsten Fließbach: Mechanik. 3. Auflage, Spektrum Akademischer Verlag, Heidelberg 1999, ISBN 3-8274-0546-7
• Herbert Goldstein, Charles Poole, John Safko: Classical mechanics. International Edition, 3. Auflage, Pearson/Addison Wesley, Upper Saddle River, N.J., 2002, ISBN 0-321-18897-7

Weblinks

Wikibooks: Die Mechanik starrer Körper – Lern- und Lehrmaterialien

• Trägheitsmomente geometrischer Körper bei Matheplanet – Anleitungen zum Berechnen diverser Trägheitsmomente mit Beispielen.
• Umrechner für Trägheitsmomente – Kleines Programm um Trägheitsmomente in amerikanische Maßeinheiten und zurück zu rechnen.