Stochastic order

Stochastic orders are order relations for random variables . They generalize the concept of bigger and smaller to random sizes and serve, for example, to compare risks in the insurance industry . The theory of stochastic orders is a more recent mathematical branch and has undergone strong development in the last few decades and is widely used in financial mathematics , economic research and operations research . Special stochastic orders were already researched in the post-war period, the first comprehensive monograph on the subject by Dietrich Stoyan was published in 1977. Numerous stochastic orders, each with different areas of application, are considered; the theory of integral orders makes it possible to investigate different orders with uniform methods.

Order in the middle

An ad-hoc order often used in practice arises from the comparison of expected values . The real random variable is said to be on average smaller than the random variable if the following applies. This order does not take into account any further properties of the distributions such as variance or skewness . ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \mathbb {E} [X]<\mathbb {E} [Y]}$

Ordinary stochastic order

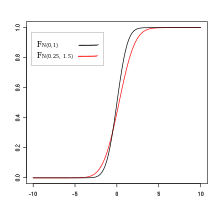
A special role is played by ordinary stochastic order ( Engl. : Usual stochastic order ). Based on the need to be able to make evaluations and decisions even under uncertainty, it transfers the clear concept of order of real numbers (formalized by the axioms of order of real numbers ) to real-valued random variables. It was examined before other stochastic orders and used in mathematical work in 1947 (Mann and Whitney) and 1956 (Lehmann). She was introduced to Operations Research by Samuel Karlin in 1960. In economic literature it is known as first order stochastic dominance .

N (0, 1) ≼ N (0.75, 1).

N (0, 1) and N (0.25, 1.5) are not comparable.

Definition : Let and be real random variables. is greater than or equal to the usual stochastic order if holds for all ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle b\in \mathbb {R} }$

${\displaystyle \mathbb {P} (X\geq b)\leq \mathbb {P} (Y\geq b)}$.

That is, for any bound , the values ​​of lie with greater (or equal) probability than the values ​​of . As a symbol is often introduced. This can also be formulated as a criterion for the distribution functions and : ${\displaystyle b}$ ${\displaystyle Y}$ ${\displaystyle b}$ ${\displaystyle X}$ ${\displaystyle X\preceq _{st}Y}$ ${\displaystyle F_{X}}$ ${\displaystyle F_{Y}}$

${\displaystyle F_{X}(b)\geq F_{Y}(b)}$for everyone . ${\displaystyle b\in \mathbb {R} }$

An equivalent definition is

${\displaystyle X\preceq _{st}Y:\Leftrightarrow \mathbb {E} [f(X)]\leq \mathbb {E} [f(Y)]}$for all monotonously growing functions . ${\displaystyle f\in C_{b}(\mathbb {R} )}$

This definition can be generalized in a natural way for random variables with values ​​in a topological space on which a partial order is defined (whereby the order must be compatible with the topology and therefore the closure of the set is required.) ${\displaystyle E}$ ${\displaystyle \leq }$ ${\displaystyle \{x\leq y,x,y\in E\}}$

Let be two random variables with values ​​in a semi-ordered Polish space . The von Strassen theorem says that if and only if there is a monotonous coupling between the variables . This means that two (other) random variables and exist which have the same distribution as resp. own and for which also applies. The proof of this existence statement is not constructive except in simple cases. ${\displaystyle X,Y}$ ${\displaystyle X\preceq _{st}Y}$ ${\displaystyle {\tilde {X}}}$ ${\displaystyle {\tilde {Y}}}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \mathbb {P} ({\tilde {X}}\leq {\tilde {Y}})=1}$

Random quantities with the same expected value and different distribution cannot be compared with the usual stochastic order, depending on the application it is necessary to consider other stochastic orders.

Integral orders

Many stochastic orders of interest (for random variables with values ​​in an ordered Polish space ), like the usual stochastic order, can be (with ) classes of "test functions" ${\displaystyle E}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}\subset \{f\colon E\rightarrow \mathbb {R} ,f\ {\text{borel-messbar}}\}}$

${\displaystyle (\star )\quad X\preceq _{\mathcal {F}}Y:\Leftrightarrow \mathbb {E} [f(X)]\leq \mathbb {E} [f(Y)]}$for all for which both expected values ​​are defined ${\displaystyle f\in {\mathcal {F}}}$

define. Such stochastic systems are called integral systems , ie the of stochastic generated order , their generator . The operation defined in this way is not necessarily transitive . One way to get around this problem is to restrict it to functions and random variables for which all expectation values ​​exist. ${\displaystyle \preceq _{\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle \preceq _{\mathcal {F}}}$

This is a probabilistic concept formation - that is, it only depends on the distributions of and on and integral orders can also be defined for distributions on ordered Polish spaces equipped with the -algebra of Borel sets: ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle (E,\tau ,\leq )}$ ${\displaystyle \sigma }$

${\displaystyle P\preceq _{\mathcal {F}}Q:\Leftrightarrow \mathbb {\int } fdP\leq \int fdQ}$for all for which both integrals are defined, ${\displaystyle f\in {\mathcal {F}}}$

where probability measures are on . ${\displaystyle P,Q}$ ${\displaystyle (E,{\mathcal {B}})}$

Often an order is already generated by a subclass of (so it is sufficient to check the right side of for some of the functions in order to conclude), in the case of the ordinary stochastic order, for example, for all isotonic measurable indicator functions or for all infinite often differentiable isotonic functions. ${\displaystyle {\mathcal {F}}}$ ${\displaystyle (\star )}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle X\preceq _{\mathcal {F}}Y}$

In applying the order it is often of interest to deduce from the left side of the validity of the right side for a certain function . The question of which functions this is possible led AW Marshall in 1991 to the concept of the maximum generator . ${\displaystyle (\star )}$ ${\displaystyle f_{0}}$

When determining a maximum generator, as with securing transitivity, a restriction to certain functions is required. A weight function is introduced and only limited functions and dimensions with respect to which can be integrated are considered. ${\displaystyle b:E\rightarrow [0,\infty )}$ ${\displaystyle b}$ ${\displaystyle \{f\colon \sup _{x\in E}|{\frac {f(x)}{b(x)}}|<\infty \}}$ ${\displaystyle b}$

Stop-loss order

The stop-loss order, which is important for actuarial mathematics, is another example of an integral order. It is generated by the class of real functions of the form , . The stop-loss order is weaker than the usual stochastic order and is used, among other things, when comparing damage amounts and as a criterion when choosing a premium principle . If and are interpreted as risks, it means that the stop-loss reinsurance premium for the risk is greater than that for each choice of the deductible . ${\displaystyle \preceq _{sl}}$ ${\displaystyle x\mapsto (x-a)^{+}}$ ${\displaystyle a\in \mathbb {R} }$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X\preceq _{sl}Y}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle a}$

Dependency orders

On a measure space , consider two random vectors and from , then we compare the covariances ${\displaystyle (\Omega ,P)}$ ${\displaystyle (X_{1},X_{2})}$ ${\displaystyle (Y_{1},Y_{2})}$ ${\displaystyle \Omega \to \mathbb {R} ^{2}}$

${\displaystyle \operatorname {Cov} (X_{1},X_{2})\leq \operatorname {Cov} (Y_{1},Y_{2})}$

a comparison of the degree of mutual dependence of the components of the two vectors is possible. Depending orders (Engl. Dependence orders ) generalize this concept and include of interest to the insurance industry, where accumulation and depending on risks such as hail or flood damage pose a financial risk for the insurer and the traditionally made in the actuarial assumption of independence of the risks leads to an underestimation of the probability of ruin.

The super-modular order belongs to the dependency orders . It is generated by the class of the supermodular functions ${\displaystyle \preceq _{sm}}$

${\displaystyle {\mathcal {F}}_{sm}:=\{f\in C^{2}(\mathbb {R} ^{n},\mathbb {R} )\colon \partial _{i}\partial _{j}f(x)\geq 0\;\forall x\in \mathbb {R} ^{n},1\leq i<j\leq d\}}$. With this definition, every twice continuously differentiable real-valued function that is defined on the real numbers is already supermodular. This in turn has the consequence that only -value random vectors can be compared with respect to which have the same marginal distributions . ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \preceq _{sm}}$

Together with the stop-loss order, it enables multivariate risk portfolios to be compared with dependent risks.

More precisely applies: Be and two risk portfolios with the same marginal distributions . If the vector of the risks of the portfolio supermodular is smaller than that of the portfolio , the random variable of the loss amount of the portfolio is smaller than that of the portfolio with regard to the stop-loss order , and thus also the price of a stop-loss reinsurance : ${\displaystyle X=(X_{1},\dots ,X_{n})}$ ${\displaystyle Y=(Y_{1},\dots ,Y_{n})}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle Y}$

${\displaystyle X\preceq _{sm}Y\Rightarrow \sum _{i=1}^{n}X_{i}\preceq _{sl}\sum _{i=1}^{n}Y_{i}}$.

literature

• Alfred Müller, Dietrich Stoyan : Comparison methods for stochastic models and risks. Wiley, Chichester 2002, ISBN 0-471-49446-1 .
• Klaus D. Schmidt: Actuarial Mathematics. 2nd, revised edition. Springer, Berlin et al. 2005, ISBN 3-540-29097-4 .
• Dietrich Stoyan: Qualitative Properties and Estimates of Stochastic Models. License issue. R. Oldenbourg, Munich et al. 1977, ISBN 3-486-21271-0 .
• R. Szekli: Stochastic Ordering and Dependence in Applied Probability (= Lecture Notes in Statistics. Vol. 97). Springer, New York et al. 1995, ISBN 0-387-94450-8 .

Individual evidence

1. ^ Alfred Müller, Dietrich Stoyan: Comparison methods for stochastic models and risks. Wiley, Chichester 2002, ISBN 0-471-49446-1 , p. 2.
2. ^ Albert W. Marshall: Multivariate Stochastic Orderings and Generating Cones of Functions. In: K. Mosler, M. Scarsini (Eds.): Stochastic Orders and Decision under Risk (= IMS Lecture Notes - Monograph Series. Vol. 19). Institute of Mathematical Statistics, Hayward CA 1991, ISBN 0-940600-26-9 , pp. 231-247.
3. ^ Nicole Bäuerle, Alfred Müller: Modeling and Comparing Dependencies in Multivariate Risk Portfolios. In: ASTIN Bulletin International Actuarial Association. Vol. 28, No. 1, 1998, ISSN  0515-0361 , pp. 59-76, here p. 62, (pdf; 812 KB) .
4. ^ Nicole Bäuerle, Alfred Müller: Modeling and Comparing Dependencies in Multivariate Risk Portfolios. In: ASTIN Bulletin International Actuarial Association. Vol. 28, No. 1, 1998, ISSN  0515-0361 , pp. 59-76, here p. 64, (pdf; 812 KB) .