Digital controller

In the series production of control devices, digital controllers are increasingly being used instead of analog controllers because they have various technical advantages. These include: one-time hardware development effort, simple parametric system changes using software, implementation of more complex controller structures, multitasking .

In most of the control systems , the controlled systems are continuously acting analog single-variable systems that can behave linearly, non-linearly and with dead time. For these control loops certain physical variables such as temperature, power, pressure, speed, level should be controlled so on. The controllers required for this can have an analog or digital system structure.

In the simplest case, digital control involves sampling and digitizing the control difference over time. In the same sampling interval, a microcomputer calculates e.g. B. the necessary control algorithm with the help of difference equations. The digital output variable of the controller, the manipulated variable, is analogized by converters and memories for the mostly analog controlled systems. Other terms of digital control refer to this process as "time-discrete control" or also as "sampling control".

Both analog and digital controllers require the control deviation as an input signal and a controller algorithm that determines the desired dynamics of the closed control loop.

Digital controllers are implemented by microcomputers . The computer needs input and output interfaces for digital signal processing in order to be able to scan the continuous input signal cyclically and to be able to calculate it digitally with special programming languages. The microcomputer processes the sampled signal values ​​as input sequences with the aid of difference equations to output sequences . The manipulated variable portions of each component of the output sequence, calculated in this way, are again supplied to the continuously operating control system as a finely graded, quasi-continuous signal via a D / A converter and a memory holding element.

Basics of numerical calculation and control

Behavior of the analog controllers

The system behavior of continuously acting linear, dynamic transmission systems is described by ordinary differential equations with constant coefficients. Using the Laplace transformation, the terms of the differential equation can be transferred to the complex image area (s area) as a transfer function with the ratio of the output signal to the input signal as a fractional-rational equation:

${\displaystyle G(s)={\frac {Y(s)}{U(s)}}={\frac {{\text{Zählerpolynom}}\ (s)}{{\text{Nennerpolynom}}\ (s)}}}$

With the determination of the zeros, the polynomials of the transfer function can be broken down into the product representation with individual elementary systems of the first order (linear factors). This form in the s-domain allows the solution of the differential equation with the inverse transformation into the time domain and, moreover, statements of the system behavior, the system stability, the system analysis and the system synthesis.

Analog standard regulators process continuous signals and usually consist of operational amplifiers with RC voltage dividers , which create an impedance ratio that is free of feedback. The associated system behavior in the complex frequency range can be written directly as the ratio of the impedances as a transfer function G (s) or G (jω). ${\displaystyle s=\delta +j\omega }$

In the case of analog controllers, the hardware components, e.g. B. Operational amplifiers with RC circuitry, the solution of the differential equation of the control algorithm.

→ Main article : regulator

Behavior of the digital controller

Discrete-time linear dynamic systems are characterized by the fact that the internal system states are only defined at individual points in time and discrete-time signals occur at the inputs and outputs. They play an important role in information technology and digital signal processing and are described in the form of sequences of numbers.

• Hardware digital input / output signals

The calculation algorithm of a digital computer does not allow continuous calculation of analog time-dependent signals. Therefore, the analog input signals, z. B. the system deviation , with the help of an (ideal) scanner and an A / D converter as scanned . The sampling of the continuous signal of the control deviation with the sampling frequency requires, in addition to the A / D converter, a functionally small hold function (sample-and-hold process), which must ensure that the microcomputer can also reliably record the digitized value. ${\displaystyle e(t)=w(t)-y(t)}$ ${\displaystyle \delta }$ ${\displaystyle e_{(k)}}$ ${\displaystyle e(t)=w(t)-y(t)}$ ${\displaystyle f_{A}=1/T_{A}}$

The desired system transfer behavior of the digital controller is calculated for the given input sequence with difference equations and is output synchronously as an output signal with numerical values. If an analog output signal is required, special hardware with a D / A converter with a hold function (hold element) allows conversion into a stepped, quasi-continuous output signal u (t) as the control variable of the controller. ${\displaystyle u_{(k)}}$

• Microcomputer as a digital controller

In the case of time-discrete systems, the input signal of a dynamic system consists of numbered elements of the input sequence (sequence of values) and the output signal of elements of the output sequence (sequence of values). In the case of the digital controller, this sequence of values ​​in the input sequence is calculated using difference equations to form subsequent elements of the output sequence. The difference equations of the digital controller determine the dynamic behavior of the entire control loop with the control algorithm and the manipulated variable in the form of calculation points of the output sequence over the controlled system. With the control variable , an approximation of the desired analytical function of the control loop behavior is achieved at the time interval between the sampling time . ${\displaystyle k=(0,1,2,3,\dots ,\infty )}$ ${\displaystyle u_{(k)}}$ ${\displaystyle y_{(k)}}$ ${\displaystyle T_{A}}$ ${\displaystyle f(t)}$

Since technical control systems often have analog inputs, the output sequence of the microcomputer must be converted into a quasi-analog signal using suitable hardware.

The number of followers of the scan is not limited. In the case of a control, an infinite number of follow-up elements are executed at real intervals of the sampling time . However, only a current program line with difference equations for calculating value sequences of the actuator and a previous program line with the difference equations for calculating the value sequences are required and saved , provided that the difference equations are 1st order. Only the current values ​​of the calculated difference equations and the values ​​of a previous calculation of the difference equations are saved temporarily. Further previous program lines with value sequences are not required and are deleted. ${\displaystyle k=(0,1,2,3,\dots ,\infty )}$ ${\displaystyle T_{A}=\Delta t}$ ${\displaystyle u_{(k)}}$ ${\displaystyle u_{(k-1)}}$

For comparison: When simulating a control loop with a personal computer, all the results of the difference equations are stored at intervals with the numbered program lines as a table with lines. The function and safety of a control loop are checked with the simulation, because if the parameters are incorrectly set and the control loop is unstable, the controlled system can be damaged. ${\displaystyle \Delta t}$ ${\displaystyle k=(0,1,2,3,\dots ,k_{\mathrm {max} })}$ ${\displaystyle k_{\mathrm {max} }}$

• Difference equations

Various methods are used to set up most of the difference equations, such as the simple Euler segment method or the better and more complex multi-step method . The more complicated multi-step methods advantageously require a significantly smaller number of subsequent equations for the same exact calculation result.

A difference equation is a numerically solvable calculation rule for a discretely defined sequence of subsequent equations which calculate variables for consecutive numbered events or numbered points in time at an interval . ${\displaystyle k=[0,1,2,3,\dots ]}$ ${\displaystyle y_{(k)}}$ ${\displaystyle \Delta x}$

The recursive solution of a first-order difference equation takes place from an initial condition through numbered sequential equations, which each refer to the result of a previous sequential equation. In the case of higher-order difference equations, each current sequential equation relates to several of the previous sequential equations, according to the ordinal number.

The general form of a recursive difference equation (Euler backward) for a first-order dynamic system is:

${\displaystyle y_{(k)}=y_{(k-1)}+f\ [u_{(k)};\Delta t;\ {\text{System}}]}$

A value of the output variable, the previous output variable, the input variable, a time interval, “system” corresponds to the form of a modified differential equation of a linear factor with a difference quotient. ${\displaystyle y_{(k)}}$ ${\displaystyle y_{(k-1)}}$ ${\displaystyle u_{(k)}}$ ${\displaystyle \Delta t}$

In the case of the first-order difference equations that occur frequently, only one program line for calculating the current output variable and the program line for the previous calculation are saved. Each output variable relates recursively to the previous output variable as an input variable. Within a series of difference equations of a program line, the output variable of one difference equation is the input variable of the next difference equation of the same program line. ${\displaystyle y_{(k)}}$ ${\displaystyle y_{(k-1)}}$

• Identification of the controlled system

Transmission elements are preferably analyzed as linear factors in a time constant representation by identifying the behavior of the controlled system over time. Using a personal computer, a simulation is used to determine the behavior of the controller and that of the system by calculating difference equations. ${\displaystyle G(s)}$

${\displaystyle \to }$For more in-depth information on system identification, see article Controlled system # Experimental system identification of controlled systems according to the step response

• Simulation of the control loop

Whether the numerical calculation of a dynamic system is a digital controller or a control loop simulation on the personal computer with many difference equations of subsystems, the only difference is that the input signal e (t) of the digital controller with hardware components an input sequence must be sampled with the sampling period . ${\displaystyle e_{(k)}}$ ${\displaystyle T_{A}}$

When simulating a control device, each individual dynamic system is recursively calculated using a difference equation in a personal computer. For each given input signal, a current output signal is calculated using difference equations of a program line and refers to a previous value of the program line . All dynamic subsystems of a program line recursively determine a calculation point of the manipulated variable at a time interval . ${\displaystyle y_{(k)}}$ ${\displaystyle y_{(k-1)}}$ ${\displaystyle \Delta t}$ ${\displaystyle u{(k)}}$

Each dynamic subsystem is described by a difference equation within a program line. The program lines correspond to finite numbered sequences , which represent an approximation of the time behavior of the original function of the control loop for an observation period. ${\displaystyle k=(0,1,2,3,\dots ,k_{\mathrm {max} })}$ ${\displaystyle k_{\mathrm {max} }\cdot \Delta t}$ ${\displaystyle f(t)}$

All results of all differential equations of the controller, the controlled system, the controlled variable and the control deviation are saved as a table for lines. ${\displaystyle k_{\mathrm {max} }}$

• Parameterization of the digital controller

The simulation of a control loop and the work of a digital controller in connection with a controlled system are similar in terms of the use of difference equations.

Depending on the desired control algorithm, a program line contains several differential equations, advantageously in product representation, because differential transfer elements of the controller can compensate for the delayed transfer elements of the controlled system. This greatly simplifies the parameterization of the digital controller by equating the time constants of the differentiating components of the controller with those of the delay elements of the controlled system.

Sequence of values ​​by scanning signals

In mathematics, a list of finite and infinitely many consecutively numbered objects is called a sequence . The same object can appear several times in a sequence.

The scanning sequence means a numbering of the following elements of the value sequence of the input signal (input sequence) and the output signal (output sequence) of a system. ${\displaystyle k=(0,1,2,3,\dots )}$

A sequence of values ​​consists of or many follow-up elements. The object with the number i is called the i-th follower or i-th component of the sequence. ${\displaystyle k_{\mathrm {max} }}$ ${\displaystyle k=\infty }$

Sampling of a time-dependent signal. * Input sequence = standardized jump, * system: PT1 element, * output sequence . ${\displaystyle u_{(k)}}$ ${\displaystyle y_{(k)}}$

The signal sampling of continuous signals f (t) requires hardware components such as idealized samplers and A / D converters, the digitized signals of which are processed into manipulated variable signals in the microcomputer as follow-up elements of the sequence of values. ${\displaystyle \delta }$ ${\displaystyle e_{(k)}}$

The period of a continuous sampling sequence of an analog or digitized input signal is usually referred to as (also and ). This function differs from the discrete time of a simulation of a dynamic system on the computer in that the period of the sampling for a value sequence is a real time and works continuously and cyclically without a limited number of follow-up elements. The values ​​of the time-discrete parameter and the sampling time can be identical. ${\displaystyle T_{A}}$ ${\displaystyle T_{0}}$ ${\displaystyle T}$ ${\displaystyle \Delta t}$ ${\displaystyle T_{A}}$

A sequence of values ​​with subsequent elements can be stored and listed in a digital computer. With an infinite number of subsequent elements in the sequence of values, such as occur when using digital controllers, this is neither possible nor necessary. ${\displaystyle k_{\mathrm {max} }}$

In online operation of a digital controller, the number of subsequent elements in the input and output sequence is unlimited. ${\displaystyle k}$

• Example of a system deviation sequence with the sampling time : ${\displaystyle T_{A}}$

Sampling of the control difference e (t) to a value sequence of the controller input: ${\displaystyle e_{(k)}}$

${\displaystyle e(t)=w(t)-y(t)\ \longrightarrow \ e(k\cdot T_{A})=e_{(k)}=[e(0),e(T_{A}),e(2T_{A}),e(3T_{A}),\dots ]}$

When calculating the subsequent elements of the input sequence with difference equations for the calculation algorithm of the "Euler Backward" method, only two current subsequent elements of the output value sequence with the following indexes are required: ${\displaystyle u_{(k)}}$

• Current value of the subsequent element of the output sequence , ${\displaystyle u_{(k_{i})}}$
• Previous value of the subsequent member of the output sequence . ${\displaystyle u_{(k_{i}-1)}}$

With the calculation of the following elements of the input sequence with difference equations the values ​​of the following elements of the output sequence of the controller result:

${\displaystyle u_{(k)}=[u(0),u(T_{A}),u(2T_{A}),u(3T_{A}),\dots ]}$

• Example of the sampling sequence of a step function G (s) = 1 / s:

The standardized signal input variable e (t) has the value 1.

The value sequence of the step function has the values:

${\displaystyle e_{(k)}=[1(0);1(T_{A});1(2T_{A});1(3T_{A})\cdots ]}$

• Example of the value sequence of a pulse function: ${\displaystyle \delta }$

The normalized signal input variable e (t) of the pulse has the value 1 for the sequence zero. All other values ​​of the sequences are zero. ${\displaystyle \delta }$

Scan sequence ${\displaystyle k=(-2,-1,0,1,2,3,\dots ]}$

Sequence of values ${\displaystyle e_{(k)}=[0(-2T_{A}),0(-T_{A}),1(0),0(T_{A}),0(2T_{A}),0(3T_{A}),\dots ]}$

Note: When using difference equations according to the Euler backward method with the function of the upper sum, the following element of the -pulse has the value at time t = 0 and k = 0 . Difference equations of the sub-sum can not capture this value . ${\displaystyle \delta }$ ${\displaystyle 1(0)}$ ${\displaystyle 1(0)}$

Sampling theorem

In the case of an ideal sampler in conjunction with an A / D converter, an analog signal becomes a sequence of numbers that is generated at a time interval T _A. If the digitized sampling values ​​are close to one another in relation to the dynamics of the analog signal at a high sampling frequency, the digitized signal exactly follows the course of the analog signal. Little information is thus lost through the scanning.

Depending on the microcomputer used, fast controlled systems do not allow arbitrarily high resolutions of the sampling process of an analog signal, because both the limit frequency of the interfaces is reached and the microcomputer can no longer provide the computing power.

In practice, real signals consist of a mixture of many frequencies.

The question now arises as to which minimum sampling frequency is required so that, for example, an analog sinusoidal signal can be sampled without any major loss of information. A harmonic sinusoidal signal cannot be distinguished from the original by sampling and reconstruction if the sampling frequency is at least twice as high as the original frequency . ${\displaystyle f_{A}=1/T_{A}}$ ${\displaystyle f_{N}}$ ${\displaystyle f_{A}}$ ${\displaystyle f_{N}}$

This connection was already recognized by the physicist Harry Nyquist as the so-called Nyquist frequency . ${\displaystyle f_{N}}$

${\displaystyle f_{A}>2\cdot f_{\mathrm {max} }}$

The Nyquist-Shannon sampling theorem states that a harmonic, analog band-limited frequency signal must be sampled with a frequency of at least so that it can be reconstructed exactly from the time-discrete signal. ${\displaystyle f_{\text{max}}}$ ${\displaystyle 2\cdot f_{\text{max}}}$

Due to frequency overlaps such as signal interference, considerable differences to the analog signal can occur during the reconstruction of the sampled signal. In practice, a low-pass filter (anti-aliasing filter) connected upstream of the A / D converter must therefore be provided to reduce higher frequency components in order to avoid misinterpretations . So that the low-pass filter does not have to have too steep edges, a sampling frequency is selected that is significantly above the theoretical value . In practice, the sampling frequency is chosen 5 to 10 times . ${\displaystyle f_{A}}$ ${\displaystyle 2\cdot f_{\mathrm {max} }}$ ${\displaystyle f_{A}}$ ${\displaystyle f_{\mathrm {max} }}$

If the sampling frequency _falls below twice the amount of f _max , the aliasing effect occurs (also known as aliasing effects, or aliasing for short).

Regulation in the offline and online process

Completely different methods of using numerical calculation are involved in the simulation of a dynamic system, e.g. B. a control loop or a digital controller that acts on an analog, continuous controlled system to differentiate.

Simulation of control loop systems (offline process)

Dynamic systems such as control loops, controlled systems and controllers can consist of different subsystems with different time behavior as a series connection, parallel connection or as a feedback circuit.

For the calculation of the input-output behavior of transmission systems or the simulation of control loops, commercial computer programs are available. With the well-known programs such as MATLAB and Simulink, extensive instruction sets are available for the theoretical modeling of dynamic systems and many special control commands.

Alternatively, with any self-created computer programs for difference equations with the discrete time Δt (also sampling time T _A ) in connection with logical operations, linear and non-linear system simulations can be carried out very efficiently.

Linear dynamic systems, as well as the components of the control loop, are clearly described as transfer functions in the time domain with differential equations and in the s-image domain . The elementary dynamic subsystems of the transfer function can be broken down into factors (linear factors) from the numerator and denominator polynomials of the transfer functions by determining the zeros. This creates the known four elementary systems of the first order, I-element, D-element, PT1-element and PD1-element of the image area, which are described in the time domain by differential equations. The difference equations of the time-discrete area are created by exchanging the differential quotients for difference quotients . ${\displaystyle f(t)}$ ${\displaystyle G(s)}$ ${\displaystyle f(k\cdot \Delta t)}$

With the use of difference equations, a mathematical approximation method is given in small time steps , which means a considerable simplification for solving differential equations. ${\displaystyle \Delta t}$

Analogy of the block diagrams of a control loop in the s area and time-discrete area.

The output signal of a dynamic system or a control loop for a given input signal is calculated in a digital computer ( personal computer ). For this purpose, the elementary systems of an overall system are calculated one after the other as a function of an input signal with difference equations in such a way that an output signal of an elementary system is the input signal of the following elementary system. All results of the subsystems up to the initial system are shown as one calculation line.

If the overall system is the simulation of a control loop, then all subsystems of the overall system are calculated one after the other in one line using difference equations of the controller and the controlled system for one subsequent element each. The output follower corresponds to a calculated value of the controlled variable . All calculated subsystems for one subsequent element each relate to the same value of k and to the previous value k-1. The following element of the controlled variable calculated in this way corresponds to the treatment of an open control loop. The control loop is closed with the relation of the control deviation , which is at the beginning of the calculation line. ${\displaystyle y_{(k)}}$ ${\displaystyle e_{(k)}=w_{(k)}-y_{(k-1)}}$

The same calculation of the individual systems of the overall system then takes place with the next calculation line as the next following element with the next higher sequence number of k. Each individual follow-up element to be calculated according to the difference equations used within this line again relates to the previous follow-up element k-1.

This results in a total of lines and follow-up parts: ${\displaystyle k_{\mathrm {max} }+1}$

${\displaystyle y(k\cdot T_{A})=y_{(k)}=[y(0),y(T_{A}),y(2T_{A}),y(3T_{A}),\dots ,y{(k_{\mathrm {max} }T_{A})}]}$

The calculation result is a table stored in the computer, the columns of which are e.g. B. successively reproduces the calculation results of the individual subsystems, the lines correspond to the number of subsequent members from to and contain identical equations. ${\displaystyle k(0)}$ ${\displaystyle k_{\text{max}}}$

The first line of the equations of the control deviation as well as all subsystems of the controller and the controlled system is specified once and copied 100-1000 times depending on the desired resolution of the controlled variable of the data. A graph for the course of y (t) or any other partial result can be generated automatically from this data.

The result is a saved tabular log of all calculation lines and calculation points of the subsystems and the system output variable.

If the controlled system contains a dead time , this can be taken into account by suitable program commands - backward shifting of the following elements of the value sequence by - steps - of the controlled system simulation. ${\displaystyle T_{t}}$ ${\displaystyle \left.k-{\frac {T_{t}}{\Delta t}}\right|_{T_{t}\gg \Delta t}}$

This calculation process with the result of a tabular listing of the calculation lines with the following elements of the scanning sequence from to is not time-dependent, but depending on the calculation speed of the computer, the total calculation result is immediately available. The discrete time between the following elements of the scanning sequence and is taken into account as a parameter (numerical value) in the difference equations and is not real time. ${\displaystyle k=0}$ ${\displaystyle k_{\mathrm {max} }}$ ${\displaystyle \Delta t}$ ${\displaystyle k_{i}}$ ${\displaystyle k_{i}-1}$

A chronologically closed graduation (rectangular course) of the output variables is not necessary. In a diagram , the course of the output variable can be shown as a closed line for the period if there is a sufficient number of subsequent elements of the value sequence (calculation points) . ${\displaystyle y(t)=f(k\cdot \Delta t)}$ ${\displaystyle k_{\mathrm {max} }\cdot \Delta t}$

If a control loop is treated with this method, which presupposes that a mathematical model of the controlled system is available, it is a control loop simulation that is ideally suited for the controller design to find the required controller parameters.

Any computer program can be used. It is recommended to use the spreadsheet because it eliminates programming errors and includes a graphical representation of the signal curves.

Digital controllers for analog continuous controlled systems (online process)

If control loops contain systems which only transmit their signals at discrete points in time, they are time-discrete control systems or sampling controls. The sampling of signals can usually be carried out continuously, but also randomly or according to a rule.

In continuous systems, differential equations describe the system behavior; in time-discrete systems, it is the difference equations derived from the differential equations that enable time-discrete sampling and calculation of the system input signal according to the system dynamics to an output variable.

The continuous sampling of the input signal is referred to as the sampling sequence. Each subsequent element of the scanning sequence corresponds to a value which is calculated in a microcomputer to form a manipulated variable value within the output sequence.

Digital controllers as well as analog controllers require a signal of the system deviation from the reference variable minus the fed back controlled variable. The microcomputers ( microcontrollers ) used require suitable input and output interfaces to calculate the mostly analog signals. These are usually analog-to-digital converters (A / D converters) that sample and digitize the input signal at discrete times. The result of the signal sampling of the control deviation can also be viewed as modulated delta pulse trains for up to different amplitudes. ${\displaystyle k=0}$ ${\displaystyle k=\infty }$

Signal flow diagram of a control loop with a digital controller and a controlled system with continuous timing.
• Using difference equations, the microcomputer calculates the value sequences of the input to output sequences synchronously.
• One element of the output sequence of the microcomputer is a calculation point approximating the analytical function.
• The task of the actuator is to supply energy, which can have a time response.
• The influence of disturbance variables within the controlled system is dealt with in the article control loop .

The digital signals calculated according to a control algorithm are output via a digital-to-analog converter (D / A converter), which is followed by a holding element (sample-and-hold method). The output signal is held by the holding stage until the next following element in the output sequence, so that an analogue stepped controller output signal can be passed on to a power interface of the actuating device for the controlled system. The sampled input variable of the input sequence must also be held (fast holding element function) until the digitization of the input signal and the transfer to the microcomputer has been completed. With this measure, the digital output signal can be converted as a continuous, stepped, quasi-analog output signal and transferred to the controlled system as a manipulated variable via a power unit.

A quantization of the input signal to a signal pulse sequence (time quantization) and the amplitude (amplitude quantization) is linked by the sampler and the A / D converter. The microcomputer processes and calculates the digitized signal sequences of the input variable into a digital output manipulated variable sequence . ${\displaystyle e_{(k)}}$ ${\displaystyle u_{(k)}}$

The task of the digital controller within a control loop is to calculate the input signal of the control deviation after each sampling using difference equations and logic commands as a control algorithm so that the output signal of the controlled system, the controlled variable, approaches the reference variable after a desired, mostly asymptotically stable course.

The difference equations required to determine the dynamic behavior of the controller as a function of the discrete time and the scanning sequence are created using the simplest method of the Euler backward method by replacing the differential quotients of the controller's system differential equation with difference quotients. ${\displaystyle k=(0,1,2,3,\dots )}$

A digital controller is constantly in use and thus carries out an unlimited number of calculated follow-up elements in the output sequence. For the calculation with difference equations (Euler backward method) for the calculation of the subsequent elements of the output sequence - from the elements of the input sequence - the computer must always provide a subsequent element of the sequence (current value) and the subsequent element of the previous sequence (previous value) . ${\displaystyle k_{i}}$ ${\displaystyle k_{i}-1}$

For digital processing, the period between two subsequent elements of the calculation sequence is usually referred to as the sampling time (also or ), which corresponds to a real time, instead of the parameters of the discretized time . The input signal sampled and digitized at the sampling frequency is then calculated as a controller algorithm using the difference equations of the output signals. ${\displaystyle \Delta t}$ ${\displaystyle T_{A}}$ ${\displaystyle T_{0}}$ ${\displaystyle T}$ ${\displaystyle f_{TA}=1/T_{A}}$ ${\displaystyle e_{(k)}}$ ${\displaystyle k}$ ${\displaystyle u_{(k)}=f({\text{System}},{\text{Eingangssignal}}\ e_{(k)},\ u_{(k-1)},\ T_{A})}$

Difference equations of the control algorithm of the digital controller calculate the sampled input signals : ${\displaystyle e_{(k)}}$

${\displaystyle e_{(k)}=(e_{(0\cdot T_{A})},\ e_{(1\cdot T_{A})},\ e_{(2\cdot T_{A})},\ e_{(3\cdot T_{A})},\dots )}$

continuously unlimited with each scan. With the help of a sampler and A / D converter, the microcomputer processes the analog control deviation from subsequent elements of the input sequence, which are sampled and calculated synchronously with the sampling time . ${\displaystyle T_{A}}$

The calculation of the input sequence with difference equations gives the output sequence:

${\displaystyle u_{(k)}=(u_{(0\cdot T_{A})},\ u_{(1\cdot T_{A})},\ u_{(2\cdot T_{A})},\ u_{(3\cdot T_{A})},\dots )}$.

Since the controlled system usually has a continuous analog behavior, there is a D / A conversion of the digital output variable at the microcomputer output with a downstream holding element for the duration . This creates a quasi-constant, stepped, analog signal as a manipulated variable at a distance from the calculated subsequent elements. ${\displaystyle T_{A}}$ ${\displaystyle T_{A}}$

Each sampling, as well as the calculation process itself, requires a finite time before a control or calculation can be carried out within the sampling sequence. This time behavior results in a lagging time shift compared to the original curve of the input variable, which is noticeable as a dead time. Whether this dead time is negligible depends on the size of the dominant time constant of the controlled system.

The advantage of the increasingly used digital controllers compared to analog controllers is:

• One-time hardware development effort
• versatile adaptation to any complex control tasks via software,
• Advantage of the complex controller structures:
  • State controller, adaptive controller, predictor controller, dead-beat controller, multitasking with one controller for different controlled systems,
• high static accuracy can be achieved, if required,
• Cost-benefit advantage, especially in systems with large numbers of pieces that do not require any hardware changes when parameters or structure changes.
• Highly integrated microcomputers for the application of control tasks with functions such as sampling elements, A / D converters, D / A converters and holding stages are already commercially available.

Disadvantages of the digital controller:

• Quantization errors can occur
• dead time connected by sampling and computing time,
• Material and time expenditure for small quantities.

Definition of the numerical calculation

Influence of the size of the time interval ∆t on the calculation (Euler backward) of a control loop with difference equations.

Discrete time

The following definitions are set here to identify the physical differences in time discretization:

• ${\displaystyle \Delta t}$is a discrete time parameter, not real time. is z. B. used in the calculation of the difference equations. ${\displaystyle \Delta t}$
• ${\displaystyle T_{A}}$(also or ) is a real time with which a continuous signal is sampled in time with . ${\displaystyle T_{0}}$ ${\displaystyle T}$ ${\displaystyle T_{A}}$

The time discretization of a dynamic time-invariant transmission system means the transition from the computation of a continuous system with infinitely high resolution to a system with a finite resolution of a continuous constant time interval . The sequence describes a finite number of subsequent members for a numerical calculation (simulation) on the computer. ${\displaystyle f(t)}$ ${\displaystyle f(k;\Delta t)}$ ${\displaystyle \Delta t}$ ${\displaystyle k=(0,1,2,3,\dots ,k_{\mathrm {max} })}$

The time interval must be sufficiently small so that dominant system movements can also be recorded, or the approximation error compared to the course of the analytic function is small. The interval must be smaller than the parameter of the smallest system time constant , otherwise calculation errors will result. should be one hundredth to one thousandth of the dominant system time constant. ${\displaystyle \Delta t}$ ${\displaystyle \Delta t}$ ${\displaystyle T_{\mathrm {min} }}$ ${\displaystyle \Delta t}$

Control algorithm of digital standard controllers (Euler reverse)

In the offline and online application for the standard controllers, the difference equations of the simplest form can be used according to the “Euler backward” route train method.

This method has the advantage of operating with simple difference equations, but has the disadvantage in the online application that the smaller the sampling time and the increasing accuracy required, the number of recursive calculations for a fixed observation period increases proportionally. Regardless of this, the smaller the sampling time, the larger the ratio to the equivalent dead time (digitization, computing time, holding element) of the hardware interfaces. Whether there is a time and cost problem depends on how large the dominant system time constant, the sampling time of the control deviation and the response time of the controller hardware components are. ${\displaystyle T_{A}}$

Numerical stability

Two conditions apply to the numerical stability and the calculation accuracy of the simulation: In order to avoid the numerical instability, the gain cannot be selected to be infinitely high, although theoretically up to two delay elements would also be possible with continuously acting control loops. Condition: If the loop gain of a control loop simulation is very large, it must be less than . is the product of all individual gains, is the dominant system time constant. is the smallest system time constant. ${\displaystyle K}$ ${\displaystyle \Delta t}$ ${\displaystyle T_{D}/K}$ ${\displaystyle K}$ ${\displaystyle T_{D}}$ ${\displaystyle T_{\mathrm {min} }}$

Accuracy of the numerical simulation

The accuracy of the numerical calculation of a dynamic system compared to the analytical function when using the Euler backward method increases linearly with the decreasing time interval in relation to the dominant system time constant . ${\displaystyle \Delta t}$ ${\displaystyle T_{D}}$

The approximation error compared to the analytic function is . The time interval must be smaller than the smallest system time constant to be calculated. Otherwise, additional errors will occur. . ${\displaystyle F_{A}}$ ${\displaystyle F_{A}\approx {\frac {\Delta t\cdot 100\,\%}{T_{D}}}}$ ${\displaystyle \Delta t}$ ${\displaystyle \Delta t\ll T_{D};\qquad \Delta t<T_{\mathrm {min} }}$

Difference equations of linear time-invariant transmission systems

Basics of system behavior

A system is a functional unit with at least one signal input and one signal output. If the system has a temporal behavior due to mostly concentrated energy storage, it is called a dynamic system . Static systems have no energy storage and therefore no time behavior.

Dynamic systems are described by different forms of differential equations. Not all differential equations can easily be solved analytically.

Technical systems can behave in a time-dependent, time-independent, linear, non-linear, continuous and discontinuous manner. The well approximated input-output behavior of these systems can be numerically solved relatively easily with computers by means of difference equations.

In the case of continuous dynamic systems, the time behavior is replaced by time-discrete behavior with the help of difference equations . Through the discretization of the signals, the input and output value sequences are created at a time interval by means of punctual sampling . ${\displaystyle \Delta t}$

Difference equations generally refer to the differential quotients of an ordinary differential equation, which are replaced by difference quotients , thus creating a numerically solvable difference equation that approximates the differential equation. ${\displaystyle \Delta y/\Delta t}$

Nonlinear and linear dynamic systems can be combined with suitable difference equations. The non-linearity is defined by logical functions or table values.

Difference equations can also refer to static, time-independent systems, in which the system input variable is discretized and the system output behavior is calculated using logical functions.

Examples of linear, non-linear and time-independent systems

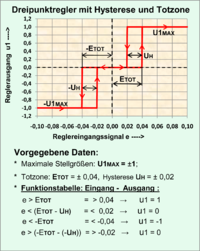
Step response linear system of the first order, pole = negative real	Step response Linear system of the 2nd order with complex conjugate poles	Non-linear system (switching regulator with hysteresis and linear system of the first order)	Time-independent system (three-point controller with hysteresis and dead zone)
Solution with first order difference equation	Solution with difference equation 2nd order	Calculation with log. Commands and difference equation 1st order	Calculation with log. Commands: IF-THEN-ELSE instruction

Basics of the difference equations of linear time-invariant systems

There are various mathematical methods for describing and converting time-continuous systems into time-discrete systems.

Difference equations mostly arise from a system-describing ordinary differential equation, whose differential quotients are replaced by difference quotients. The continuous mathematical operations of integration and differentiation are approximated in a time-discrete manner by forming sums and differences.

Depending on an input value sequence and the dynamic system, difference equations calculate the output value sequence with the sequence that represents a numbering of the values. ${\displaystyle k=0;1;2;3;\dots }$

A distinction must be made between the use of a simulation of a time-discrete dynamic system as a function of an input signal and the use of a real hardware system, the input signal of which is sampled at time intervals . ${\displaystyle T_{A}}$

• Simulation: To use a simulation on the digital computer, the input signal for the time parameter is discretized and the output sequence for is calculated using the difference equation of the dynamic system . This recursive difference equation always refers to previous output value sequences and is recalculated as often as required - depending on the required accuracy. The result is a sequence of values ​​(calculation points) stored in a table in the computer at a time interval , which can also be represented graphically as a function of the discrete input signal and the system transmission behavior. ${\displaystyle \Delta t}$ ${\displaystyle k\Delta t}$ ${\displaystyle \Delta t}$
• Signal sampling : With a given hardware system, the input signal is sampled at intervals of the sampling time , digitized and fed into a microcomputer as a sequence of input values. This system is usually the control algorithm as a difference equation. The output sequence is analogized and in a holding element z. B. zero order. This creates a stepped, quasi-constant signal that can be processed as a manipulated variable by a continuously operating controlled system. ${\displaystyle T_{A}}$

With the approximation algorithm for a small time interval, the difference equations describe the signal changes at the output of a system (simplified notation ) after each time interval as a function of the relevant system (e.g. linear factors in the s range) and the input signal . With the continuous repetition of the calculation with the time interval and addition of the change results to the previous result , the signal curve of a system over time is obtained . ${\displaystyle \Delta t}$ ${\displaystyle y(k\Delta t)}$ ${\displaystyle y_{(k)}}$ ${\displaystyle u_{(k)}}$ ${\displaystyle \Delta t}$ ${\displaystyle y_{(k-1)}}$ ${\displaystyle y_{(k)}}$ ${\displaystyle k_{\mathrm {max} }\cdot \Delta t}$

The solution of the system behavior of a dynamic system with difference equations always corresponds to the total solution as the addition of the homogeneous and particulate solution. Without initial values ​​it is the particulate solution. If initial values ​​of the system are available, the normal control form of the state space representation can be used to solve the system's difference equations. The solution rule is already included in the difference equations without initial values.

Difference equations can also arise with the help of the z-transformation .

Linear factors of the transfer function G (s)

Difference equations of the simplest kind relate to the first-order differential equations belonging to the linear factors of the transfer function G (s), the differential quotients of which are replaced by difference quotients.

Linear factors are created by decomposing polynomials of the numerator and denominator of a transfer function G (s) as a fractional-rational function. This relationship is of great importance because there are only three different forms of first and second order linear factors and systems of higher order contain only combinations thereof.

By determining the zeros , the polynomials of the transfer function can be brought into a product form ( linear factors ) in the numerator and denominator. The poles (zeros of the denominator) or zeros (zeros of the numerator) are either zero, real or conjugate complex . The product representation in the numerator and denominator of the transfer function is mathematically identical to the polynomial representation in the numerator and denominator. ${\displaystyle G(s)}$ ${\displaystyle G(s)}$

Ready-made programs for determining the zeros of a polynomial up to the 4th order can be found on the Internet under the call "Determine zeros (solutions) of polynomials". For systems of the 2nd order, the “pq formula”: can be used to calculate the conjugate complex zeros. ${\displaystyle x^{2}+px+q=0}$ ${\displaystyle x_{1},x_{2}}$

Linear factors of the pole zero representation

Example of the decomposition of the polynomials of the transfer function by determining the pole zero position into real linear factors:

${\displaystyle G(s)={\frac {Y(s)}{U(s)}}={\frac {b_{0}+b_{1}\cdot s+b_{2}\cdot s^{2}+\cdots +b_{m}\cdot s^{m}}{a_{0}+a_{1}\cdot s+a_{2}\cdot s^{2}+\cdots +a_{n}\cdot s^{n}}}:=k\cdot {\frac {(s-s_{n1})(s-s_{n2})\dotsm (s-s_{nm})}{(s-s_{p1})(s-s_{p2})\dotsm (s-s_{pn})}}}$

Since the linear factors of the numerator and denominator of the transfer function are identical, the zeros and poles are denoted by for a simplified representation . Negative real parts of the poles and zeros of the linear factors mean stable elementary systems, positive real parts mean unstable elementary systems. ${\displaystyle s_{0}}$

• In the case of linear factors of the first order, the zeros or poles are real numerical values. Stable systems contain negative real parts. ${\displaystyle s_{n}}$ ${\displaystyle s_{p}}$
• Second order linear factors with conjugate complex zeros or poles are combined into quadratic terms for easier calculation, in which only real coefficients occur.
• Linear factors are mostly converted into the time constant representation by the reciprocal formation of the zeros and poles.

Product term in the time constant representation with a negative value of the zero : ${\displaystyle s_{n}}$

${\displaystyle \underbrace {(s-s_{n})} _{\text{Produktterm}}\ :=\underbrace {(s+a)} _{\text{Produktterm}}=\ \underbrace {a\cdot ({\frac {1}{a}}\cdot s+1)} _{a\ {\text{ausgeklammert}}}\quad :=\underbrace {K\cdot (T\cdot s+1)} _{\text{Zeitkonstanten-Darstellung}}\qquad {\bigg |}\quad a=negativerNullstellenwert.}$

In linear control technology, it is a welcome fact that practically all regular (phase-minimal) transfer functions or frequency responses of control loop elements can be written or traced back to the following three basic forms ( linear factors ). They have a completely different meaning, depending on whether they are in the numerator (differentiating behavior) or in the denominator (delaying, integrating) of a transfer function.

Depending on the numerical values ​​of the coefficients a and b in the polynomial representation, the products can take the following three forms in the time constant representation:

Type linear factor	Meaning in the counter	Meaning in the denominator
${\displaystyle G_{1}(s)=T\cdot s}$ (Zero position = 0)	Differentiator, D-member	Integrator, I-link
${\displaystyle G_{2}(s)=T\cdot s+1}$ (Real zero)	PD link	Delay, PT1 element
${\displaystyle G_{3}(s)=T^{2}\cdot s^{2}+2\cdot D\cdot T\cdot s+1}$ (Zeros conjugate complex)	PD2 element: for 0 < D <1	Vibration link PT2 link : for 0 < D <1

Here, T is the time constant, s is the complex frequency, D degree of damping.

The transfer function of a dynamic transfer system can contain single and multiple linear factors in the numerator and denominator. ${\displaystyle G(s)=Y(s)/U(s)={\text{Zähler}}(s)/{\text{Nenner}}(s)}$

${\displaystyle \to }$For more in-depth information on differential equations, transfer functions, the origin of the linear factors, see control engineering # Basics of the transfer function as a system description

Origin of the difference equations

Rectangular approximation of a PT1 element by calculation with a difference equation according to Euler backwards (upper sum).

Usually the explicit Euler backward method of rectangular approximation is used as the simplest method to set up the difference equations. According to this method, difference equations can be formed from the associated differential equations of the 4 elementary systems G (s) of the first order of the transfer functions by introducing approximately the difference quotient instead of the differential quotient . ${\displaystyle dy/dt}$ ${\displaystyle {\frac {\Delta y}{\Delta t}}={\frac {y_{(k)}-y_{(k-1)}}{\Delta t}}}$

As a rule, it is assumed that the internal system memories of the transmission system are in the idle state and that the initial values ​​at t = 0 for and all derivatives are zero. ${\displaystyle y_{(0)}=0}$ ${\displaystyle y_{(0)}}$

The output variable of a calculated time-discrete system with the help of difference equations is called in simplified notation of the indexing as . ${\displaystyle y(k\cdot \Delta t)}$ ${\displaystyle y_{(k)}}$

In the offline application - for example the simulation of a control loop with an input sequence and an output sequence - the following elements of the value sequence are limited to a certain number and refer to the period . After calculating the following elements of the input sequence with difference equations, the output sequence with its following elements is created as a solution that approximates the associated differential equation. ${\displaystyle u_{(k)}}$ ${\displaystyle y_{(k)}}$ ${\displaystyle k_{\mathrm {max} }}$ ${\displaystyle k_{\text{max}}\cdot \Delta t}$ ${\displaystyle u_{k}}$ ${\displaystyle y_{(k)}=(y_{(0\cdot \Delta t)},\ y_{(1\cdot \Delta t)},\ y_{(2\cdot \Delta t)},\ y_{(3\cdot \Delta t)},\dots ,\ y_{(k_{\mathrm {max} }\cdot \Delta t)})}$

The following links are created without scanning. Due to the recursive application of the difference equation, each calculation refers to the previous result . The repeated application of the same difference equations ends at . ${\displaystyle y_{(k)}}$ ${\displaystyle y_{(k-1)}}$ ${\displaystyle k_{\mathrm {max} }}$

In the online application with a digital controller, the sampled input sequence is calculated with difference equations, then the following elements of the output sequence of the controller are created . The calculation is done with digitized values ​​synchronously in the cycle of . A continuous control signal is usually required for the controlled system. Sequences of values ​​can be converted to a stepped, quasi-continuous signal with the aid of an A / D converter and a holding element. ${\displaystyle e_{(k)}}$ ${\displaystyle u_{(k)}=(u_{(0\cdot T_{A})},\ u_{(1\cdot T_{A})},\ u_{(2\cdot T_{A})},\ u_{(3\cdot T_{A})},\dots )}$ ${\displaystyle T_{A}}$

The disadvantage of the Euler backward method for fast controlled systems with a good approximation to the analytical system function is the high number of sampling sequences, which does not play a role in the offline simulation of a dynamic system with a digital computer, but in online operation. As the accuracy of the approximation to the transmission behavior of the system increases, the period of the sampling must decrease and the computing power increases linearly.

Other methods of numerical calculation are used for a better approximation z. B. instead of the rectangle method ( explicit Euler method ), the trapezoidal surface method ( Heun method ), the multi-step method ( Runge-Kutta method ) and other methods. The reason for the more complex approximation method and thus the more extensive difference equations is the higher accuracy that can be achieved and thus a reduction in the recursion sequences, which can be necessary for slow microcomputers and their interfaces for real-time calculations.

Example of the creation of a difference equation of integration (I-term) from the differential equation:

The transfer function of the I-element is: ${\displaystyle \ G(s)={\frac {Y(s)}{U(s)}}={\frac {1}{T_{I}\cdot s}}}$ The corresponding differential equation is: ${\displaystyle T_{I}\cdot {\dot {y}}(t)=u(t)}$ The difference quotient is used in place of the differential quotient : ${\displaystyle {\dot {y}}(t)}$ ${\displaystyle T_{I}\cdot {\frac {y_{(k)}-y_{(k-1)}}{\Delta t}}=u_{(k)}}$ The modified difference equation of the I term thus reads : ${\displaystyle y_{(k)}}$ ${\displaystyle y_{(k)}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T_{I}}}}$ In the same way, the difference equations of the standard controllers can be derived from the associated differential equations.

Table of the difference equations (Euler backward) of the elementary systems G (s) first order

Elementary systems	Transfer function	Difference equations
P element	${\displaystyle {\frac {Y}{U}}(s)=K}$	${\displaystyle y_{(k)}=K\cdot u_{(k)}}$
I-link	${\displaystyle {\frac {Y}{U}}(s)={\frac {1}{T\cdot s}}}$	${\displaystyle y_{(k)}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T}}}$
D link	${\displaystyle {\frac {Y}{U}}(s)=T\cdot s}$	${\displaystyle y_{(k)}=[u_{(k)}-u_{(k-1)}]\cdot {\frac {T}{\Delta t}}}$
PD 1 link	${\displaystyle {\frac {Y}{U}}(s)=K\cdot (T\cdot s+1)}$	${\displaystyle y_{(k)}=K_{PD1}\cdot \left[u_{(k)}+(u_{(k)}-u_{(k-1)})\cdot {\frac {T}{\Delta t}}\right]}$
PT 1 link	${\displaystyle {\frac {Y}{U}}(s)={\frac {K}{T\cdot s+1}}}$	${\displaystyle y_{(k)}=y_{(k-1)}+[K_{PT1}\cdot u_{(k)}-y_{(k-1)}]\cdot {\frac {\Delta t}{T+\Delta t}}}$

(With K = gain factor, = current discrete-time output variable, = previous output variable, T = time constant, = current discrete-time input variable) ${\displaystyle y_{(k)}}$ ${\displaystyle y_{(k)}=y_{(k-1)}}$ ${\displaystyle u_{(k)}}$

These difference equations of elementary systems can be meshed multiplicatively, additively or fed back as required. Each equation of an overall system is calculated one after the other. When subsystems are connected in series, the calculated output variable is the input variable for the following subsystem. When sub-systems are connected in parallel, the results of the output variables are added together. ${\displaystyle y_{(k)}}$ ${\displaystyle u_{(k)}}$

Determination of the difference equations from the controller transfer function G (s)

The transfer functions of the controller and the associated elementary difference equations can be assigned directly. The transfer functions of a controller can be defined in series and parallel display. This also applies to the associated difference equations in the operator representation . These different equations for calculating the controller output variable for each in the s range Y (s) and each in the discrete-time range are mathematically identical. ${\displaystyle G_{R}(s)}$ ${\displaystyle y_{(k)}=\cdots }$ ${\displaystyle y_{(k)}}$

The implementation of the transfer function in operator representation of the series representation of the control algorithm of the elementary systems was chosen because the series representation of the PI and PID controllers contain PD1 elements for each. For the controller design, the parameter determination is simplified because the PD1 elements of the controller can directly compensate the delays of PT1 elements of the controlled system with the same time constants and thus simplify the controlled system. ${\displaystyle Y(s)=U(s)\cdot G(s)}$

${\displaystyle (T_{V}\cdot s+1)/(T_{n}\cdot s+1)=1|\qquad {\text{für}}\ T_{V}=T_{N}}$

PI and PID controllers are described with several elementary difference equations in the numerator and denominator. It is therefore not possible to describe the difference equations with one equation when converting from the s-domain to the time-discrete domain. These difference equations are calculated one after the other. It should be noted that in the series representation of the difference equations, the output quantity of the first difference equation is the input quantity of the next difference equation.

If you define a PID controller with the parameters and the parallel display in the s range , you get a sum equation of the transfer function. If this equation is converted into a common numerator (s) and denominator (s), the polynomial representation of the transfer function results. With the determination of the zeros in the numerator and denominator, this equation can be converted into the product representation and a transfer function with two PD1 elements and an I element can be recognized. It is important that the parameters and have disappeared and the time constants of the two PD elements are replaced by other z. B. and be determined. ${\displaystyle K_{PID},\ T_{N}}$ ${\displaystyle T_{V}}$ ${\displaystyle T_{N}}$ ${\displaystyle T_{V}}$ ${\displaystyle T_{1}}$ ${\displaystyle T_{2}}$

For the practice of the PID controller design, the transfer function of the PI controller of the series representation is better suited, to which a further PD element with the time constant is assigned multiplicatively . This avoids complicated parameter conversions. ${\displaystyle T_{V}}$

The difference equations associated with the components of the transfer function G (s) are shown in the table below.

The previous signal designations with the input variable and the output variable correspond to the commonly used designations in system theory. The input signal for difference equations and the output signals apply to the controller . The controller output variable after the D / A interface is for the stepped, quasi-continuous signal . ${\displaystyle U(s)}$ ${\displaystyle Y(s)}$ ${\displaystyle e_{(k)}}$ ${\displaystyle u_{(k)}}$ ${\displaystyle u(t)}$

The gain factors of the controller components of the difference equations are taken into account for an I element as follows: ${\displaystyle K_{PI}}$

${\displaystyle u_{(k)}=u_{(k-1)}+K_{PI}\cdot e_{(k)}\cdot \Delta t/T_{N}}$

Note: The quotient already corresponds to a gain factor. ${\displaystyle 1/T_{N}}$

The gain factor of the controller components of the difference equations is taken into account in a PD element as follows: ${\displaystyle K_{PD}}$

${\displaystyle u_{(k)}=K_{PD}\cdot [e_{(k)}+(e_{(k)}-e_{(k-1)})\cdot T_{V}/\Delta t]}$

Difference equations of the standard controllers

Table of the difference equations of the standard controllers (Euler backward)

Controller type and test signals	Transfer function	Difference equation
Test signal pulse function	${\displaystyle {\hat {u}}_{e\delta }(t)={\frac {1}{\Delta t}}}$ U (s) = 1	Amplitude: Amplitude: ${\displaystyle u_{(k=0)}={\frac {1}{\Delta t}}}$ ${\displaystyle u_{(k>0)}=0\,}$
Test signal step function	U (s) = 1 / s	${\displaystyle u_{(k)}=1}$
Test signal rise function	U (s) = 1 / s²	${\displaystyle u_{(k)}=u_{(k-1)}+c\cdot \Delta t}$ Constant of rise c = Δ u / Δ t
Control deviation	${\displaystyle E(s)=W(s)-Y(s)}$	${\displaystyle e_{(k)}=w_{(k)}-y_{(k-1)}}$
P controller	${\displaystyle {\frac {U}{E}}(s)=K}$	${\displaystyle u_{(k)}=e_{(k)}\cdot K}$
I controller	${\displaystyle {\frac {U}{E}}(s)={\frac {1}{T_{N}\cdot s}}}$	${\displaystyle u_{(k)}=u_{(k-1)}+e_{(k)}\cdot {\frac {\Delta t}{T_{N}}}}$
PI controller parallel structure PI controller series structure	${\displaystyle {\frac {U}{E}}{(s)}=K_{PI}\cdot \left(1+{\frac {1}{T_{N}\cdot s}}\right)}$ ${\displaystyle {\frac {U}{E}}{(s)}=K_{PI}\cdot {\frac {T_{N}\cdot s+1}{T_{N}\cdot s}}}$	Representation of the controller series structure: ${\displaystyle {\text{I-Glied:}}\quad e_{1(k)}=e_{1(k-1)}+{e_{(k)}\cdot K_{PI}\cdot \Delta t}/{T_{N}}}$ ${\displaystyle {\text{PD-Glied:}}\quad u_{(k)}=e_{1(k)}+[e_{1(k)}-e_{1(k-1)}]\cdot {T_{N}}/{\Delta t}}$
PD 1 controller	${\displaystyle {\frac {Y}{U}}(s)=K_{PD1}\cdot (T_{V}\cdot s+1)}$	${\displaystyle u_{(k)}=K_{PD1}\cdot \left[e_{(k)}+\left[e_{(k)}-e_{(k-1)}\right]\cdot {\frac {T_{V}}{\Delta t}}\right]}$
PID controller parallel structure PID controller series structure	${\displaystyle {\begin{aligned}{\frac {U}{E}}{(s)}&=K_{PID}\cdot {\Big (}1+{\frac {1}{T_{N}\cdot s}}+T_{V}\cdot s{\Big )}\end{aligned}}}$ ${\displaystyle {\frac {U}{E}}{(s)}=K_{\text{PID}}\cdot {\frac {(T_{1}\cdot s+1)(T_{2}\cdot s+1)}{s}}}$	Representation of the controller series structure: ${\displaystyle {\text{I-Glied:}}\quad e_{1(k)}=e_{1(k-1)}+{e_{(k)}\cdot K_{PI}\cdot \Delta t}/{T_{N}}}$ ${\displaystyle {\text{PD-Glied 1:}}\quad e_{2(k)}=e_{1(k)}+[e_{1(k)}-e_{1(k-1)}]\cdot {T_{1}}/{\Delta t}}$ ${\displaystyle {\text{PD-Glied 2:}}\quad u_{(k)}=e_{2(k)}+[e_{2(k)}-e_{2(k-1)}]\cdot {T_{2}}/{\Delta t}}$

${\displaystyle T_{N}}$= Reset time, = lead time, = P gain, = discrete time or sampling time. ${\displaystyle T_{V}}$ ${\displaystyle K}$ ${\displaystyle \Delta t=T_{A}}$

${\displaystyle \to }$For more information on the difference equation, see the article on the difference equation

Difference equations as a function of the upper and lower sums

Definition of the upper sum and lower sum of the numerical integration.

In numerical mathematics, the areas of the rectangle approximation to a given analytic function mean as the upper sum when the upper edge of the rectangle is above the analytic function. Conversely, it is the lower sum if the upper edge of the rectangle touches below the analytic function. For the numerical calculation, it is not the area of ​​the rectangles that is of interest, but the position of the course of the upper edge of the right approximation.

The subsequent elements of the output sequence calculated with difference equations can be defined as a function of the upper sum and the lower sum. The results of difference equations are sub-elements of the sequence of values ​​in time intervals and thus calculation points of a function, but do not mean a closed function curve. Only with a digital controller in which a subsequent element of the output sequence flows via an A / D converter into a zero-order holding element for the period , the holding element being deleted with each step, does a closed function sequence arise. ${\displaystyle \Delta t=T_{A}}$ ${\displaystyle T_{A}}$

The functional difference between the upper sum and the lower sum means, for example, that an input signal is effective as a single pulse at the time and sequence in a time-discrete dynamic system for the period - i.e. between and . Difference equations after the sub-sum can not capture this pulse. ${\displaystyle \delta }$ ${\displaystyle t=0}$ ${\displaystyle k=0}$ ${\displaystyle T_{A}}$ ${\displaystyle k=0}$ ${\displaystyle k=1}$ ${\displaystyle \delta }$

The sequence of values ​​of the output sequence of the function of the lower sum calculated with difference equations differ from those of the upper sum in that the sequence of values ​​of the lower sum is delayed by a subsequent step.

Basics of digital controllers with the help of z-transformation (online process)

The interfaces of the digital controller including the sampling with the holding stage are identical to the procedure listed above.

The z-transformation arose from the Laplace transformation in order to transform sampling sequences for the digital system calculation and thus to make them calculable. The z-transform is a transform of sample sequences that has properties similar to the Laplace transform for the treatment of differential equations. With the methods of z-transformation, difference equations of scanned signal sequences can be determined.

In connection with the interfaces to a mostly continuously acting (analog) controlled system, the digital controller acts as a computer program that continuously calculates the manipulated variable at intervals of the sampling time T _A. The controller algorithm is defined with the sampling sequence and controller function as a z-transfer function.

Obtaining the control algorithm with the help of the z-transfer functions is a completely different calculation method than that of the rectangular approximation according to Euler-Backward for creating difference equations. In the z-transfer function, the discrete scan-specific time behavior of a scan sequence such as hold functions, D / A conversion, A / D conversion and computing time is combined with the desired control algorithm. The inverse z-transformation of the z-transfer function gives the required difference equation . ${\displaystyle f_{(k)}}$

According to the properties of the z-transformation , the following operations result: ${\displaystyle F(z)}$

• Special arithmetic operations:

Right shift, left shift, difference set, sum set etc., previous calculation sequences must be saved.

• Transfer of the dynamic system as z-transfer function,
• Properties of the z-image area similar to the Laplace transform:

Z-block representation of series and parallel-connected systems, pole-zero decomposition, stability analysis, calculation rules and the transfer from the z-image area to the discrete time area . ${\displaystyle f_{(k)}}$

The basic application of the z-transformation for the control algorithm is as follows:

• The sampling sequences with holding stage of the input signal are transformed as z-transfer function , ${\displaystyle H(z)}$
• The difference equation of the desired controller behavior is transformed as a z-transfer function , ${\displaystyle f_{(k\cdot T_{A})}}$ ${\displaystyle G(z)}$
• The z-transformed systems are grouped algebraically according to the z-calculation rules,
• With the inverse z-transformation of the z-product of signal and control algorithm, the calculation algorithm of the digital controller is created.

The analysis and synthesis of discrete signals and systems can be facilitated with the z-transformation, but also requires extensive mathematical special knowledge that is partly based on rules similar to those of the Laplace transformation.

${\displaystyle \to }$See also z-transformation # Application of the z-transfer function for a digital PI controller with sampling function and holding element

Strategy of the controller parameterization

Table of the design strategy of control loops when using standard controllers

function	execution
Identification of the controlled system See article Controlled system	Graph the standardized step response or standardized impulse response of the controlled system. ${\displaystyle \delta }$ Using difference equations, simulate the time behavior for first-order delay elements of the recorded step or impulse response. In the case of controlled systems with delays> 2nd order, simulate the time behavior as a dead time. Determine the gradient for controlled systems with global I behavior and simulate it using a difference equation.
Pole-zero compensation	In the s range, PD1 elements of the controller completely compensate the PT1 elements of the controlled system with the same time constants. This also applies in the time-discrete area for the system description with difference equations. The difference equations of the series structure are recommended for the PI and PID controller structures because they contain PD elements. Deviations in the time constants of the controller subsystems from the dominant subsystems of the controlled system with approx. 10% of the time constants, which can result from material aging or the difficult identification of the system model, are acceptable.
P and PD controllers	P and PD controllers are fast controllers for simple controlled systems or controlled systems with global I behavior. It should be noted that when using P and PD controllers, relatively high gains can be selected without the need for a tendency to oscillate in the control loop. It is seldom possible to achieve high P gains for a given controlled system, which leads to manipulated variable limitations. This makes the transfer behavior of the control loop sluggish and non-linear, and the transfer function G (s) of the closed control loop is therefore invalid. In the numerical simulation of the individual subsystems of the control loop with the closing condition, this effect is visible according to the stored tabular representation, if it is known from what level the control variable of the hardware control system is limited. The permissible P gain determines the size of the static control deviation for systems without I behavior.
Controller without static control deviation:	If the static control deviation is to approach zero, the controller needs an I component. I, PI and PID controllers are not fast controllers, but the P gain depends on the delays in the controlled system and on the size of any dead time that may be present. With controllers with an I component, high P gains can seldom be achieved. Because of the additional pole with a phase angle of −90 °, the control loop tends to oscillate slightly with a relatively small P gain of the controller.
Control systems with dead time	Controlled systems with a significant portion of the dead time require a PI controller or, in extreme cases, an I controller.
Setting the P gain	The P gain of the control loop with the factor K can be determined by simulation with the selected controller and the model of the controlled system to be recorded in a personal computer according to the desired parameters of the transition function (step response) of the controlled variable of a damped oscillating system.
Digital controllers for fast controlled systems:	When simulating a control loop with digital controllers, the dead time behavior of the interfaces of the microcomputer, which can be assigned to the controlled system, must be taken into account.

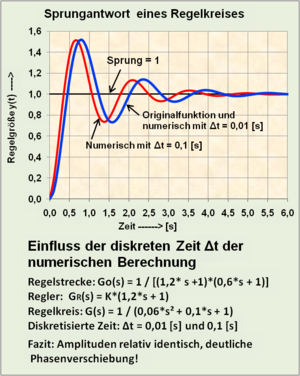
Tabular comparison of the numerical calculation methods in the offline and online process

This information reveals an essential difference between the offline process and the online process. The offline calculation of a dynamic system or a control loop consisting of a controller and a controlled system has no time behavior, it could also be carried out with a pocket calculator without impairing the accuracy. For the offline calculation (simulation) of a real control loop with a digital controller, the time behavior of the interfaces of the digital controller must be taken into account as dead time.

The online calculation of the digital controller has dead times within each sampling sequence, which result from the interfaces required for signal conversion in the input and output, in the holding element and the computing time for calculating the difference equations. As far as the control of fast controlled systems is concerned (e.g. dominant time constant = 1 s of the controlled system), fast components of the converter and the microcomputer are required to keep the substitute dead time small in relation to the dominant time constant of the controlled system and the sampling time. ${\displaystyle T_{D}}$

Numerical calculation of dynamic systems (offline process) (difference equations according to the Euler backward method )	Control with digital controllers (online process) (difference equations according to the Euler reverse method)
Dynamic system: control path or control loop. Mixed linear and non-linear systems can be simulated.	Dynamic system: digital controller acts on an analog controlled system. Digital controllers for any application are possible.
System input variable: in dynamic systems as test signal u (k), in control loops the reference variable as test signal w (k).	System input variable: If the analog control deviation e (t) = w (t) - y (t), e (t) is specified, the input sequence is sampled and digitized as e (k).
System output sequence : y (k) The output sequence are numerical values ​​of the sequence k. = simplified notation for ${\displaystyle y_{(k)}}$ ${\displaystyle y_{(k\cdot \Delta t)}}$	Controller output sequence : u (k) u (k) are numerical values ​​of the sequence k. After the D / A conversion, u (k) becomes a stepped analog variable u (t) (voltage).
Scanning sequence k means numbering of the following elements: at a distance . ${\displaystyle k=(0,1,2,3,\dots ,k_{\mathrm {max} })}$ ${\displaystyle \Delta t}$	K sampling sequence numbering means of the follower members: in the time interval T A . ${\displaystyle k=(0,1,2,3,\dots ,\infty )}$
Discrete time : is a parameter of time, not real time ${\displaystyle \Delta t}$ ${\displaystyle \Delta t}$	Sampling time : is a real time. ${\displaystyle T_{A}}$ ${\displaystyle T_{A}}$
Size of the discrete time : e.g. the dominant system time constant. ${\displaystyle \Delta t}$ ${\displaystyle \Delta t=1/100\ bis\ 1/1000}$	Size of the sampling sequence T A : e.g. the dominant time constant of the controlled system. ${\displaystyle T_{A}=\Delta t}$ ${\displaystyle T_{A}=1/10\ bis\ 1/100}$
Difference equations: e.g. B. Method Euler backward , previous computational consequence , Requires be difference Engl. the subsystems of the controller and the process. ${\displaystyle y_{(k)}=f({\text{Dyn. System}},u_{(k)},\ y_{(k-1)},\ k,\ \Delta t)}$ ${\displaystyle y_{(k-1)}}$	Difference equations: e.g. B. Method Euler backward , previous computational consequence , Requires, the difference equations of the subsystems of the digital controller. ${\displaystyle u_{(k)}=f({\text{Reglersystem}},\ e_{(k)},\ u_{(k-1)},\ k,\ \Delta t)}$ ${\displaystyle u_{(k-1)}}$
Calculation process: tabular The transfer functions of the 1st order are assigned difference equations . Each line calculates the difference equations of all subsystems. There are k max +1 elements = lines = output sequence. Only 2 changing current elements of the output sequence are relevant: and All lines are saved as a protocol. ${\displaystyle u_{(k)}}$ ${\displaystyle u_{(k-1)}}$	Calculation process: continuous The sampling sequence starts the calculation of the subsystems of the digital controller with the associated difference equations at a time interval T A. Only 2 changing current members of the output sequence are relevant: and . Each element of the output sequence is processed into a quasi-analog manipulated variable f (t). ${\displaystyle u_{(k)}}$ ${\displaystyle u_{(k-1)}}$
Interfaces: no input signal or for all sequences up to , output signal for all sequences up to . ${\displaystyle u_{(k)}}$ ${\displaystyle w_{(k)}}$ ${\displaystyle k_{(0)}}$ ${\displaystyle k_{\mathrm {(max)} }}$ ${\displaystyle y_{(k)}}$ ${\displaystyle k_{(0)}}$ ${\displaystyle k_{\mathrm {(max)} }}$	Interfaces: for analog control deviation , In input: AD converter (short holding element function) for calculation time, In output: DA converter with holding element for stepped analog manipulated variable . ${\displaystyle e_{(t)}}$ ${\displaystyle u_{(t)}}$
Dead time of the numerical calculation: none due to the method (applies to Euler backward method of the upper sum ) The dead time behavior of the controlled system can be simulated.	Dead time of the digital controller: Dead time of the AD converter Computing time of the subsystems with difference equations Dead time of the DA converter with holding element. With a certain size of the dominant time constant z. B. T> 1 s of the controlled system is a dead time z. B. of 0.01 sec mostly negligible.
Numerical stability: Condition to avoid numerical instability: If the loop gain is very large, then must be less than . is the product of all individual gains, is the dominant system time constant, is the smallest system time constant. ${\displaystyle K}$ ${\displaystyle \Delta t}$ ${\displaystyle T_{D}/K}$ ${\displaystyle K}$ ${\displaystyle T_{D}}$ ${\displaystyle T_{\mathrm {min} }}$	Numerical stability: Because of the inevitable dead times, a high P gain is not possible.
Accuracy of the numerical simulation: The accuracy increases as the time interval decreases . The approximation error compared to the analytical function is: . must be smaller than the smallest system time constant. Otherwise, error. ${\displaystyle \Delta t}$ ${\displaystyle F_{A}}$ ${\displaystyle F_{A}\approx {\frac {\Delta t\cdot 100\,\%}{T_{D}}}\qquad \Delta t\ll {T_{D}};\ \Delta t<T_{\mathrm {min} }}$ ${\displaystyle \Delta t}$	Accuracy of the numerical calculation: The accuracy increases as the sampling time decreases . Otherwise like offline process. ${\displaystyle T_{A}}$ ${\displaystyle T_{A}\ll T_{D};\ T_{A}<T_{\mathrm {min} }}$
Ideal and real controllers of the control loop simulation: They are identical.	Real digital controllers: It is not possible to convert a calculated value u (t) into a manipulated variable energy without a time delay .

See also

• Portal: measurement, control and regulation technology

literature

• Holger Lutz, Wolfgang Wendt: Pocket book of control engineering with MATLAB and Simulink . 11th edition. Europa-Lehrmittel, 2019, ISBN 978-3-8085-5869-0 .
• Gerd Schulz: Control technology 2 / multi-variable control, digital control technology, fuzzy control . 2nd Edition. Oldenbourg, 2008, ISBN 978-3-486-58318-2 .
• Jan Lunze: Control engineering 2, multi-variable systems, digital control . 7th edition. Springer Verlag, 2013, ISBN 978-3-642-10197-7 .

Web links

Wikibooks: Introduction to Systems Theory  - Learning and Teaching Materials

Individual evidence

1. ↑ Oliver Nelles: State space and digital control. ( Memento of December 27, 2016 in the Internet Archive ) (PDF) University of Siegen, July 7, 2014, accessed on March 24, 2015 Chapter: Sampling Theorem and Aliasing , p. 197 (lecture script, 286 pages).
2. ↑ Holger Lutz, Wolfgang Wendt: Pocket book of control engineering with MATLAB and Simulink . 11th edition. Verlag Europa-Lehrmittel, 2019, ISBN 978-3-8085-5869-0 , Chapter: Basic operation of digital control loops .
3. ↑ Holger Lutz, Wolfgang Wendt: Pocket book of control engineering with MATLAB and Simulink . 11th edition. Verlag Europa-Lehrmittel, 2019, ISBN 978-3-8085-5869-0 , Chapter: Basic algorithms for digital controls .
4. ↑ Oliver Nelles: State space and digital control. ( Memento of December 27, 2016 in the Internet Archive ) (PDF) University of Siegen, July 7, 2014, accessed on March 24, 2015, Chapter: Digital Controls, Introduction , Digital Control Loop , Discrete Time Systems , p. 177 ff., 185, 179 (lecture notes, 286 pages).