Bragg mirror

Three Bragg mirrors that have their stop band in the yellow, red and blue areas of the optical light and reflect this part (left). The transmitted part of the light appears in the complementary color (right).

A Bragg mirror (abbreviated DBR from distributed Bragg reflector ) is an efficient reflector that is used in light guides or in optical resonators . It consists of alternating, thin layers of different refractive indices . The layers usually consist of dielectrics . That is why the term dielectric mirror is used for such a reflector . At each boundary layer a part of the electromagnetic wave of the light is reflected according to the Fresnel formulas . If the wavelength is close to four times the optical path length of the layers, the reflected rays interfere constructively and a high-quality reflector is created. The area where the reflection is very high is called the stop band . Light with a wavelength within the stop band cannot propagate in the structure.

Characteristics

The first 4 layers of a Bragg mirror. Each layer has an optical path length of . Thus, constructive interference occurs at the wavelength of . ${\displaystyle {\frac {\lambda _{0}}{4}}}$ ${\displaystyle \lambda _{0}}$

Calculated reflectivity of an ideal Bragg mirror in the area of ​​the stop band.

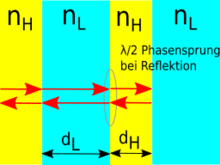
Bragg mirrors consist of alternating, dielectric thin layers with a low and high refractive index. The maximum reflectivity for a wavelength is achieved when all layers have an optical thickness of exactly a quarter of the wavelength. In the sketch on the right, 4 layers of a Bragg mirror are illustrated. If light hits the Bragg mirror perpendicularly, there is a phase shift of the electric field vector of the light by half a wavelength at the interfaces between the low and the high refractive index ( , ) . However, this is not the case with the transitions from high to low refractive index. In order to generate constructive interference of the Bragg mirror, the total phase difference must, however, be a multiple of the wavelength of the incident light. In order to achieve constructive interference at all boundary layers, the optical path length of each thin film must be. The condition for maximum reflectivity of the Bragg mirror can now be determined as follows. For constructive interference, the total phase shift must be an integral multiple of the wavelength of the incident light. ${\displaystyle n_{L}}$ ${\displaystyle n_{H}}$ ${\displaystyle {\frac {\lambda }{2}}}$ ${\displaystyle {\frac {\lambda }{2}}}$ ${\displaystyle m}$

${\displaystyle 2n_{L}d_{L}+{\frac {\lambda }{2}}=2n_{H}d_{H}+{\frac {\lambda }{2}}=m\lambda }$

The following condition thus arises for the optical path length of the thin layers of the Bragg mirror.

${\displaystyle n_{H}d_{H}=n_{L}d_{L}={\frac {(2m-1)\lambda }{4}}}$

A Bragg mirror therefore shows constructive interference at several wavelengths. So there are several wavelength ranges of constructive interference at which a maximum of the reflection occurs. The wavelength for which the maximum reflectivity is met is referred to as and lies in the middle of the so-called stop band of a Bragg mirror. The image on the right shows the calculated reflection spectrum of a Bragg mirror in the area of ​​the stop band and . The reflectivity for this wavelength becomes: ${\displaystyle m=1}$ ${\displaystyle \lambda _{0}}$ ${\displaystyle \lambda _{0}}$

${\displaystyle R=\left[{\frac {n_{o}(n_{2})^{2N}-n_{s}(n_{1})^{2N}}{n_{o}(n_{2})^{2N}+n_{s}(n_{1})^{2N}}}\right]^{2},}$

where is the index of refraction of the surrounding medium, and the index of refraction of the two materials and the index of refraction of the substrate. is the number of layer pairs. Provided that both materials have different refractive indices, results . It is therefore possible to achieve an arbitrarily high reflectivity if only enough layer pairs are used. ${\displaystyle n_{o}}$ ${\displaystyle n_{1}}$ ${\displaystyle n_{2}}$ ${\displaystyle n_{s}}$ ${\displaystyle N}$ ${\displaystyle \lim \limits _{N\to \infty }R=1}$

The frequency width of the stop band is calculated as follows: ${\displaystyle \Delta f_{0}}$

${\displaystyle {\frac {\Delta f}{f_{0}}}={\frac {4}{\pi }}\arcsin \left\vert {\frac {n_{1}-n_{2}}{n_{1}+n_{2}}}\right\vert }$.

Physical mode of action

Reflectance

Illustration of the derivation of the matrix transfer method based on a thin film on a substrate

This section explains how to calculate the reflectivity of a Bragg mirror. The reader can orientate himself on the picture on the right, where a thin film is sketched on a substrate. An electromagnetic wave is reflected at the interface between air and thin film. The incident wave and reflected wavelength have the wave vectors and . Furthermore, the wave transmitted at the first interface has the wave vector and the wave reflected at the second interface is described by. Ultimately, the wave that propagates into the substrate has the wave vector . The vectors of the magnetic field strength and the electric field strength are labeled in an analogous manner. The vectors of the magnetic field strength point into the image plane (marked by a cross) for reflected waves and out of the image plane for incoming waves (marked by a point). At the first phase transition, the following condition must apply to the corresponding amplitudes of the electric field strength vectors. This follows from the Fresnel equations, which state that the tangential components of the electric field vectors must be continuous at an interface. ${\displaystyle R}$ ${\displaystyle {\vec {k_{0}}}}$ ${\displaystyle {\vec {k'_{0}}}}$ ${\displaystyle {\vec {k_{1}}}}$ ${\displaystyle {\vec {k'_{1}}}}$ ${\displaystyle {\vec {k_{2}}}}$ ${\displaystyle {\vec {H}}}$ ${\displaystyle {\vec {E}}}$

${\displaystyle E_{0}+E_{0}'=E_{1}+E_{1}'}$

The same applies to the amplitudes of the magnetic field strength. However, since the orientation of the vectors is reversed during the reflection, the reflected amplitudes are subtracted.

${\displaystyle H_{0}-H_{0}'=H_{1}-H_{1}'}$

The amplitudes of the magnetic field strength can be expressed by the corresponding amplitudes of the electric field strength. One makes use of the relationship . The refractive index is represented, while the speed of light in vacuum and represents the magnetic permeability with is labeled. Assuming that the relative magnetic permeability for all materials involved is approximately 1, the following equations are obtained because and can be shortened. ${\displaystyle H={\frac {n}{\mu c}}E}$ ${\displaystyle n}$ ${\displaystyle c_{0}}$ ${\displaystyle \mu }$ ${\displaystyle c_{0}}$ ${\displaystyle \mu }$

${\displaystyle n_{0}(E_{0}-E_{0}')=n_{1}(E_{1}-E_{1}')}$

Thus the continuity conditions at the first interface are expressed by the amplitudes of the electric field strengths with two equations. The same can be done for the second interface. These amplitudes have and however written with an additional phase term. Both amplitudes without a phase term correspond to the conditions at the first interface. Since the wave vector of the transmitted wave points in the positive x-direction, the amplitude at the second interface is described by a positive phase shift . Since the wave vector points in the negative x-direction, the corresponding phase shift can also be recorded. In both cases, the thickness of the thin film indicates . With the help of these considerations one arrives at two equations for the second interface. ${\displaystyle E_{1}}$ ${\displaystyle E'_{1}}$ ${\displaystyle k_{1}d_{1}}$ ${\displaystyle {\vec {k'_{1}}}}$ ${\displaystyle -k_{1}d_{1}}$ ${\displaystyle d_{1}}$

${\displaystyle E_{1}e^{\mathrm {i} k_{1}d_{1}}+E_{1}'e^{-\mathrm {i} k_{1}d_{1}}=E_{2}}$

${\displaystyle n_{1}E_{1}e^{\mathrm {i} k_{1}d_{1}}-n_{1}E_{1}'e^{-\mathrm {i} k_{1}d_{1}}=n_{2}E_{2}}$

Now write both equations with imaginary and real parts:

${\displaystyle (E_{1}+E_{1}')\cos(k_{1}d_{1})+\mathrm {i} (E_{1}-E_{1}')\sin(k_{1}d_{1})=E_{2}}$

${\displaystyle n_{1}(E_{1}-E_{1}')\cos(k_{1}d_{1})+\mathrm {i} n_{1}(E_{1}+E_{1}')\sin(k_{1}d_{1})=n_{2}E_{2}}$

With the continuity conditions at the first interface explained at the beginning, the last two equations can be written in matrix form.

${\displaystyle M{\binom {E_{0}+E_{0}'}{n_{0}(E_{0}-E_{0}')}}={\binom {E_{2}}{n_{2}E_{2}}}}$

and

${\displaystyle M={\begin{pmatrix}\cos(k_{1}d_{1})&{\frac {\mathrm {i} }{n_{1}}}\sin(k_{1}d_{1})\\\mathrm {i} n_{1}\sin(k_{1}d_{1})&\cos(k_{1}d_{1})\end{pmatrix}}}$

If you finally divide by and invert the matrix to , you get the following expressions. The first equation contains the reflection coefficient and the transmission coefficient . ${\displaystyle E_{0}}$ ${\displaystyle M}$ ${\displaystyle M'}$ ${\displaystyle r={\frac {E'_{0}}{E_{0}}}}$ ${\displaystyle t={\frac {E_{2}}{E_{0}}}}$

${\displaystyle {\binom {1}{n_{0}}}+{\binom {1}{-n_{0}}}r=M'{\binom {1}{n_{2}}}t}$

${\displaystyle M'={\begin{pmatrix}\cos(k_{1}d_{1})&-{\frac {\mathrm {i} }{n_{1}}}\sin(k_{1}d_{1})\\-\mathrm {i} n_{1}\sin(k_{1}d_{1})&\cos(k_{1}d_{1})\end{pmatrix}}}$

Sketch of the calculation process for calculating the reflectivity of a Bragg mirror using the matrix transfer method

One can thus calculate both the transmission and reflection coefficients for a thin film on a substrate. In order to be able to calculate the reflectivity of a Bragg mirror, however, several positions have to be taken into account. This can be done by inserting a matrix for each thin film into the above equation. In clear terms, this means that the conditions at the first interface can be determined on the basis of the nth layer. This is illustrated in the illustration on the right. This process is called the matrix transfer method .

${\displaystyle {\binom {1}{n_{0}}}+{\binom {1}{-n_{0}}}r=M_{1}'M_{2}'\ldots M_{N-1}'M_{N}'{\binom {1}{n_{s}}}t}$

Ultimately, the above formula leads to the maximum reflectivity of the Bragg mirror at the wavelength . One makes use of the fact that at the wavelength all terms have the value of . ${\displaystyle R=r^{2}}$ ${\displaystyle \lambda _{0}}$ ${\displaystyle \lambda _{0}}$ ${\displaystyle kd}$ ${\displaystyle {\frac {\pi }{2}}}$

${\displaystyle R=\left[{\frac {n_{o}(n_{2})^{2N}-n_{s}(n_{1})^{2N}}{n_{o}(n_{2})^{2N}+n_{s}(n_{1})^{2N}}}\right]^{2}}$

Bandwidth

In the previous section it was explained that the reflection coefficient at the top layer of the Bragg mirror can be calculated using the matrix transfer method. By transforming the matrix transfer equation in the previous chapter, the following expression is obtained, which links the amplitudes of the magnetic and electrical field strengths at with the amplitudes at . The thicknesses of the first two layers of the Bragg mirror are combined here. According to the explanations in the last section, the transfer matrix is given by. ${\displaystyle z=0}$ ${\displaystyle z=d_{1}+d_{2}=d}$ ${\displaystyle d}$ ${\displaystyle M_{d}=M'_{1}M'_{2}}$

${\displaystyle {\binom {E(0)}{H(0)}}=M_{d}{\binom {E(d)}{H(d)}}}$

To continue further, one uses the Bloch theorem . The amplitudes of an electromagnetic wave in a medium with periodically varying refractive index with period length are given by their values ​​at , multiplied by a phase factor . The wave vector of the electromagnetic wave propagating in the Bragg mirror is given by. You finally arrive at the following expression: ${\displaystyle d}$ ${\displaystyle z=d}$ ${\displaystyle z=0}$ ${\displaystyle e^{iKd}}$ ${\displaystyle K}$

${\displaystyle {\binom {E(0)}{H(0)}}=e^{-\mathrm {i} Kd}{\binom {E(d)}{H(d)}}}$

Combining the first two equations in this section leads to the following eigenvalue equation :

${\displaystyle M_{d}{\binom {E(d)}{H(d)}}=e^{-\mathrm {i} Kd}{\binom {E(d)}{H(d)}}}$

The aim is now to find an expression for the wave vector . If this takes on imaginary values, the components of the electromagnetic wave decrease exponentially with the layer thickness. This means that the electromagnetic wave cannot propagate in the mirror. The range in which is imaginary corresponds to those wavelength ranges in which Bragg mirrors show their reflection maxima. In order to find an expression for depending on the wavelength, one first makes use of the fact that the determinant is 1. The determinant of a matrix is ​​at the same time given by the product of its eigenvalues. An eigenvalue is already given by, which means that the remaining one must be given. Ultimately, the trace of the matrix is defined by the sum of the eigenvalues. Using the definition of the cosine with imaginary exponential functions one finally obtains the following equation: ${\displaystyle K}$ ${\displaystyle K}$ ${\displaystyle K}$ ${\displaystyle M_{d}}$ ${\displaystyle e^{-\mathrm {i} Kd}}$ ${\displaystyle e^{iKd}}$ ${\displaystyle M_{d}}$

${\displaystyle e^{-iKd}+e^{iKd}=2\cos(Kd)=2\cos(k_{1}d_{1})\cos(k_{2}d_{2})-{\Bigl (}{\frac {n_{2}}{n_{1}}}+{\frac {n_{1}}{n_{2}}}{\Bigr )}\sin(k_{1}d_{1})\sin(k_{2}d_{2})}$

By further rearranging and expressing the wave numbers in terms of the wavelength , you also get: ${\displaystyle \lambda }$

Photonic band structure of an ideal Bragg mirror and the calculated reflection spectra with an increasing number of layers with an alternating refractive index

${\displaystyle K=\arccos \left(\cos(k_{1}d_{1})\cos(k_{2}d_{2})-{\frac {1}{2}}\left({\frac {n_{2}}{n_{1}}}+{\frac {n_{1}}{n_{2}}}\right)\sin(k_{1}d_{1})\sin(k_{2}d_{2})\right)}$

${\displaystyle K=\arccos \left(\cos \left({\frac {2\pi n_{1}d_{1}}{\lambda }}\right)\cos \left({\frac {2\pi n_{2}d_{2}}{\lambda }}\right)-{\frac {1}{2}}\left({\frac {n_{2}}{n_{1}}}+{\frac {n_{1}}{n_{2}}}\right)\sin \left({\frac {2\pi n_{1}d_{1}}{\lambda }}\right)\sin \left({\frac {2\pi n_{2}d_{2}}{\lambda }}\right)\right)}$

The last equation describes the wave vector as a function of the wavelength of the perpendicularly incident light. A plot of this is shown in the figure on the right, where the x-axis is in units of . In taking complex values, which corresponds to the peak in the reflection spectrum of the Bragg mirror. The reflection spectra of the corresponding Bragg mirrors with several thin-film layers are also shown in the picture on the right. The more layers the mirror has, the better it corresponds to an ideal Bragg mirror and the stop band agrees better with the range of complex wave vectors. Furthermore, as was deduced in the previous section, the reflectivity increases with the number of thin-film layers. ${\displaystyle K}$ ${\displaystyle K}$ ${\displaystyle {\frac {\pi }{d}}}$ ${\displaystyle {\frac {\pi }{d}}}$ ${\displaystyle K}$

An analytical expression for the width of the stop band can also be found for an ideal Bragg mirror with an infinite number of thin-film layers. Is reacted to the argument of the inverse cosine -Terms -1 or 1, as it is not defined more in the real area from these values. The phase difference is also introduced . Thus the sine and cosine terms can be grouped together, since their arguments have the same values ​​in a Bragg mirror. ${\displaystyle \delta _{e}}$

${\displaystyle -1=\cos ^{2}(\delta _{e})-{\frac {1}{2}}{\Bigl (}{\frac {n_{2}}{n_{1}}}+{\frac {n_{1}}{n_{2}}}{\Bigr )}\sin ^{2}(\delta _{e})}$

By moving you get to:

${\displaystyle \cos ^{2}(\delta _{e})={\Bigl (}{\frac {n_{1}-n_{2}}{n_{1}+n_{2}}}{\Bigl )}^{2}}$

Furthermore you can write with the help of the auxiliary variable : ${\displaystyle \delta _{e}}$ ${\displaystyle \Delta g}$

${\displaystyle \delta _{e}={\frac {\pi \lambda _{0}}{2\lambda _{e}}}={\frac {\pi }{2}}(1\pm \Delta g)}$

With the help of the last equation one arrives at:

${\displaystyle \cos ^{2}(\delta _{e})=\sin ^{2}(\pm {\frac {\pi \Delta g}{2}})}$

Finally, you get a printout for the width of the stop band. Instead of the wavelength as before, the stop band is expressed in terms of frequencies. The central frequency of the stop band is characterized while the width of the stop band. ${\displaystyle f_{0}}$ ${\displaystyle \Delta f}$

${\displaystyle {\frac {\Delta f}{f_{0}}}={\frac {4}{\pi }}\arcsin \left\vert {\frac {n_{1}-n_{2}}{n_{1}+n_{2}}}\right\vert }$

Manufacturing

The alternating layers of dielectrics of a Bragg mirror can be produced with different coating processes, on the one hand by physical vapor deposition such as sputtering or vapor deposition, on the other hand chemical vapor deposition or with the help of the sol-gel method . A further method of order Bragg mirror is the electrochemical Porösizieren of silicon - wafers . The porosity can be precisely adjusted. If the porosity is varied between high and low porosity, a sequence of layers with low and high refractive index is obtained. In contrast to the methods mentioned above, the electrochemical porosification also allows the simple realization of mirrors with continuously varying (e.g. sinusoidal) refractive index profiles. Such mirrors are called rugate filters .

application

Two dielectric mirrors in one experimental setup

Bragg mirrors are used in many semiconductor lasers such as surface emitters (VCSEL), optically pumped semiconductor lasers (VECSEL), laser diodes , DFB and DBR lasers . In many lasers , Bragg mirrors are used as mirrors because the wavelength is usually precisely defined. This means that with Bragg mirrors you can achieve significantly higher reflectivities than with metallic mirrors. In addition, Bragg mirrors can be used as dichroic mirrors , which reflect one color almost completely and transmit other colors almost completely. The use of λ / 2 instead of λ / 4 layers results in an interference filter and, if dielectric materials are used, a dielectric filter .

Bragg mirrors can also be easily integrated into glass fibers, which are referred to as fiber Bragg gratings . The same principles apply here as with other Bragg mirrors.

In addition to the fields of application described so far, the potential application of porous Bragg mirrors is a current research topic. Possible areas of application are in the field of analytical chemistry and gas sensors.

Individual evidence

1. ↑ CJR Sheppard: Approximate calculation of the reflection coefficient from a stratified medium . In: Pure and Applied Optics: Journal of the European Optical Society Part A . 4, No. 5, 1995, p. 665. bibcode : 1995PApOp ... 4..665S . doi : 10.1088 / 0963-9659 / 4/5/018 .
2. ↑ ^{a b} H. A. Macleod: Thin-Film Optical Filters . 3. Edition. Institute of Physics Publishing, Bristol / Philadelphia 2001, ISBN 0-7503-0688-2 (first edition: 1986).
3. ^ Rice University MOOC: Waves & Optics. Retrieved May 11, 2017 . 
4. ↑ ^{a b} Paul Anton Letnes: Wave propagation in layered structures - Lecture. Retrieved May 11, 2017 . 
5. ↑ Femius Koenderink: Lecture on AMOLF Institute of Materials Science. (PDF) Retrieved May 11, 2017 (English). 
6. ↑ Polina Anikeeva: Lecture notes from MIT-Electronic, Optical and Magnetic Properties of Materials. (PDF) Retrieved May 11, 2017 (English). 
7. ↑ A. Scherer, M. Walther, LM Schiavone, BP Van der Gaag, ED Beebe: High reflectivity dielectric mirror deposition by reactive magnetron sputtering . In: Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films . tape 10 , no. 5 , September 1, 1992, pp. 3305-3311 , doi : 10.1116 / 1.577816 .
8. ^ I-Wen Feng Hongxing Jiang: SiO2 / TiO2 distributed Bragg reflector near 1.5 μm fabricated by e-beam evaporation . In: Journal of Vacuum Science & Technology A . 31, 2013, p. 061514. doi : 10.1116 / 1.4823705 .
9. ↑ David Massoubre: Vertically Conductive Single-Crystal SiC-Based Bragg Reflector Grown on Si Wafer . In: Scientific Reports . 5, 2015, p. 17026. doi : 10.1038 / srep17026 .
10. ^ Rui Almeida: Photonic band gap structures by sol – gel processing . In: Current Opinion in Solid State and Materials Science . 7, No. 2, 2003, pp. 151-157. doi : 10.1016 / S1359-0286 (03) 00045-7 .
11. ↑ ^{a b} Claudia Pacholski: Photonic Crystal Sensors Based on Porous Silicon . In: Sensors . tape 13 , no. 4 , April 9, 2013, p. 4694-4713 , doi : 10.3390 / s130404694 .
12. ↑ Markus Leitgeb, Christopher Zellner, Michael Schneider, Ulrich Schmid: Porous single crystalline 4H silicon carbide rugate mirrors . In: APL Materials . 5, No. 10, 2017, p. 106106. doi : 10.1063 / 1.5001876 .
13. ^ Carl Hepburn: Vertical Cavity Surface Emitting Lasers (VCSELs). In: Britney Spears' Guide to Semiconductor Physics. Retrieved September 21, 2011 .