Fischer projection

The Fischer projection is a method to clearly map the spatial structure of a linear, chiral chemical compound in two dimensions . It was developed by Emil Fischer and is often used for molecules with several neighboring stereocenters such as sugars .
regulate

In many chemical compounds, the position of the atoms in space is decisive for their properties, which makes it necessary to differentiate between different stereoisomers . In the case of carbon compounds in particular, it is often difficult to make the spatial alignment of the up to four binding partners in the tetrahedral angle of 109.5 ° clear.
The Fischer projection solves this problem without perspective means by observing the following rules when drawing the molecule:
- A chain of carbon atoms is drawn from top to bottom, with the most heavily oxidized atom on top. According to the rules on the nomenclature of hydrocarbons, the carbon atom with the number 1 is on top. This doesn't always have to be the most heavily oxidized carbon atom, but it is in most cases. But there are also agreed exceptions such as B. galacturonic acid , which is formally an oxidized form of D- galactose . The most highly oxidized carbon atom in this case is the C atom with the number 6, and the numbering of the D- galactose is retained.
- Horizontal (horizontal) lines point out of the projection plane towards the viewer. This can also be indicated by filled wedges that become thinner towards the center.
- Vertical (vertical) lines run behind the projection plane, away from the viewer. This can also be indicated by cross-dashed wedges which also become thinner towards the center.
In addition, carbon is the implicit atom, i.e. In other words, the “C” is not written in the chiral centers in particular.

The Fischer projections of the two enantiomers of glyceraldehyde are given as an example , as well as the corresponding wedge line formulas. The stereo descriptors D and L then indicate the configuration of the lowest stereocenter, depending on whether the horizontal residue with the higher priority (here: OH> H) points to the right ( D ) or to the left ( L ). If there are several stereocenters, one can not accumulate several D s and L s (see below)
It is important to note that the actual spatial structure of chiral molecules was not known at the time of Fischer. Glyceraldehyde was used as a reference substance ("Fischer-Rosanoff Convention"): the right-handed enantiomer was arbitrarily assigned the projection with the OH residue pointing to the right and this was therefore referred to as the D configuration (Latin: dexter "right") without that you could know if this was true. If other compounds (especially sugar ) could be broken down to the dextrorotatory glyceraldehyde, they also had the D configuration under this assumption .
In 1951 Johannes Martin Bijvoet was able to show the actual spatial structure by means of the X-ray structure analysis of glyceraldehyde. The arbitrary assumption turned out to be correct by chance: The D and ( R ) configurations of glyceraldehyde are identical. From the D / L or ( R / S ) configuration, conclusions can not be drawn automatically about the angle of rotation α or the direction of rotation [(+) or (-)] of the plane of polarization of the linearly polarized light . Examples:
- In the case of tartaric acid , the D enantiomer rotates to the left and the L enantiomer rotates to the right. The rotation value α for L - (+) - tartaric acid is + 12.7 °, for D - (-) - tartaric acid -12.7 ° under the same measuring conditions.
- A single enantiomer can have a different direction of rotation depending on the pH value. For example, the amino acid L- leucine has a specific angle of rotation of + 15.1 ° (= clockwise) at room temperature in 6 molar hydrochloric acid and a specific angle of rotation of −10.8 ° (= counterclockwise) in neutral water, whereas it is in 3 molar sodium hydroxide solution turn clockwise with + 7.6 °.
- L -alanine [( S ) - alanine ] has an angle of rotation α of + 13.0 ° (c = 2 in 5 N hydrochloric acid)
- L- cysteine [( R ) - cysteine ] has an angle of rotation α of + 7.9 ° (c = 2 in 5 N hydrochloric acid)
If there are several stereocenters, the configurations of these cannot be specified one after the other (as is the case with the Cahn-Ingold-Prelog Convention, for example ). If there is more than one stereocenter, there are more than two stereoisomers, including diastereomers and enantiomers . When using the Fischer nomenclature, it is essential to give diastereomers different names:
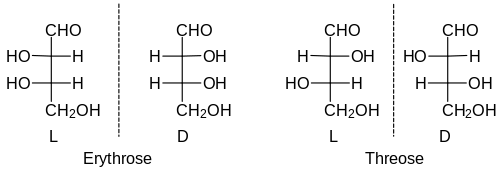
Erythrose and threose , for example, are two different sugars that differ only in the configurations at the two chiral centers. More precisely, they are diastereomers. There is one pair of enantiomers each of both. The relative configuration of the upper stereocenter is determined by the name: in erythrosis the OH groups point in the same direction, in threosis in different directions. But since z. B. C6 aldoses (including glucose ) have 4 stereocenters, there are 2 4 = 16 stereoisomers. This corresponds to eight pairs of enantiomers, so you have to remember eight different names and eight different relative configurations for this group of sugar molecules.
Examples from biochemistry for D - and L - compounds are D - glucose (grape sugar) and the amino acid L - alanine .
application
For a center of chirality
There are also a number of rules for interpreting a Fischer projection. This allows structures to be examined for isomerism without having to imagine them in three dimensions, which is often very difficult. For a projection with a central carbon and four substituents:
- Rotation by 180 ° (360 °, ...) results in the same molecule,
- Rotation by 90 ° (270 °, ...) results in the corresponding enantiomer .
- One (three, five, ...) swap (s) of two substituents each gives the enantiomer ,
- two (four, six, ...) swaps of two substituents each result in the same molecule.
It should first be noted that carbon atoms that do not have four different substituents, but at least two identical ones, a double bond or a triple bond, are not centers of chirality and are therefore superfluous for the above rules. Second, it should be noted - as trivial as it may seem - that the entire substituent must be compared in determining differences; H. if there is a propyl chain on one side and an ethyl chain on the other, the substituents are different.
For multiple centers of chirality
If there are several centers of chirality, the same rules apply to each individual center. In order to determine the isomerism of a molecule, the "interchange method" can be used. If two structures differ only in their arrangement at the centers of chirality, the following applies:
- They are exactly identical if every center is identical, i.e. two (or even zero) exchanges are necessary at each center in order to convert one structure into the other,
- They are enantiomers if and only if this applies to every center, i.e. an exchange is necessary at every center in order to convert one structure into the other,
- They are diastereomers if and only if the other two cases do not occur, i.e. H. for example, if one swap is necessary at one center and two swaps at the other.
1-Bromo-2-methyl-butan-3-ol should serve as an example:
The numbering goes from bottom to top. The lowest carbon atom, numbered as one, is achiral and is for confusion only. Carbons two and three are chiral. In the first case, center two is obviously identical, with center three two swaps are necessary, it is also identical: the molecules are identical. In the second case you need one swap at center two and two at number three: they are diastereomers. In the third case there is a reflection (an exchange at both centers), they are enantiomers.
meso shapes
In the Fischer projection one can easily see a plane of symmetry and two isomers as meso forms .
Individual evidence
- ^ Rules of Carbohydrate Nomenclature . In: The Journal of Organic Chemistry . tape 28 , no. 2 , 1963, p. 281-291 , doi : 10.1021 / jo01037a001 .
- ↑ a b Graphical representation of stereochemical configuration (IUPAC Recommendations 2006) In: Pure and Applied Chemistry . Volume 78, Issue 10, pp. 1897-1970, doi : 10.1351 / pac200678101897 .
- ^ Entry on Fischer – Rosanoff convention (or Rosanoff convention) . In: IUPAC Compendium of Chemical Terminology (the “Gold Book”) . doi : 10.1351 / goldbook.F02392 Version: 2.3.3.
- ↑ E. Broad Maier, G. Jung: Organic Chemistry , Thieme Verlag, 4th ed., 2001
- ↑ H.-D. Belitz, W. Grosch, P. Schieberle: Textbook of food chemistry. 5th edition, Springer, 2001, ISBN 3-540-41096-1 , p. 14. Restricted preview in the Google book search.
- ↑ a b Hans-Dieter Jakubke, Hans Jeschkeit: amino acids, peptides, proteins , Verlag Chemie, Weinheim, p. 30, 1982, ISBN 3-527-25892-2 .