Critical aperture

The articles aperture , iris diaphragm , critical diaphragm , entrance pupil , exit pupil and light intensity (photography) overlap thematically. Help me to better differentiate or merge the articles (→  instructions ) . To do this, take part in the relevant redundancy discussion . Please remove this module only after the redundancy has been completely processed and do not forget to include the relevant entry on the redundancy discussion page{{ Done | 1 = ~~~~}}to mark. - Alturand … D 20:16, 11 Jun. 2018 (CEST)

Fig. 1: The optimal aperture as a compromise between aberration blur and diffraction blur ; the useful aperture is not the intersection of the graphs (f (x) = g (x)), but the minimum of the sum of both functions (f '(x) = -g '(x))

Fig. 2: The resolving power of a macro lens (y-axis) as a function of the f-number (x-axis)

In photography, the critical aperture is the f-number that allows the highest resolution for taking a flat subject. The necessary aperture is the optimal aperture setting for an extended depth of field .

definition

A perfectly corrected lens has the greatest resolution when the aperture is open, i.e. with the smallest possible aperture number. The diffraction blur is the smallest here (the red line in Figure 1). With all lenses, however, are aberrations (aberrations) at open aperture is greatest (in Figure 1, the green lines). Aberrations can be carried by hiding the edge rays of the optical dimming reduced. With most lenses, the sum of blurring due to diffraction and aberrations of the lens first decreases when stopping down, and then increases again when stopping down. The minimum of the blurring, i.e. H. the maximum of the resolution is exactly at this point.

The diffraction blur is the same for all lenses for a given focal length, f-number and wavelength and cannot be influenced by the structure of the lens system. It is a property of the captured light. The optics can get the most out of it, but nothing more.

The optimum of the sharpness of detail is the point at which the increase of both functions is identical in terms of amount, but the sign is reversed. Then the sum is minimal. The optimum is not necessarily at the intersection of the two functions - this is almost always shown incorrectly. This point is called the critical aperture.

Another almost common mistake is equating the blurring of a circular disk with the diameter d and an Airy disk with the diameter d of the first zero crossing. The latter creates far less blurring.

With fixed lenses this aperture depends on the image circle radius. In the center of the image, many modern lenses achieve the optimum without or with little stop-down, while more stop-down is required at the edge of the image.

In the case of zoom lenses , the critical aperture is still dependent on the set focal length and usually increases continuously after a short drop in the lower focal length range to longer focal lengths.

For 35mm format lenses, the critical aperture is usually between f / 4 and f / 11. In Figure 2, the critical aperture from measured values ​​of a real macro lens is shown graphically as the maximum of the curve at an aperture number of f / 5.6. Lenses of smaller formats reach the critical aperture with smaller f-numbers, often with an open aperture. Microscope objectives almost always have their critical aperture at an open aperture and cannot be stopped down directly.

Here again the components considered:

• critical aperture: diffraction + aberration of a given lens = minimal
• beneficial aperture: diffraction + aberration of a given lens + depth of field of a given subject = minimal

Calculation on a plano-convex lens

Back focal length x in an optical imaging with a plano-convex, spherical lens with the refractive index n = 1.5 and the radius of curvature at a given height of incidence . ${\displaystyle R}$ ${\displaystyle H}$

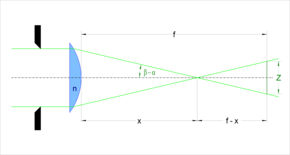
The critical aperture can be illustrated relatively easily using a plano-convex, spherical lens . If one looks at an optical image from infinity with parallel, monochromatic light of the wavelength through such a lens with the radius of curvature and the focal length , the situation shown in the adjacent illustration results. ${\displaystyle \lambda }$ ${\displaystyle R}$ ${\displaystyle f}$

By diffraction arises in the image plane of a diffraction disk having the diameter

${\displaystyle d=2,44\cdot \lambda \cdot {\frac {f}{D}}=2,44\cdot \lambda \cdot k}$

where the entrance pupil of the optical image and ${\displaystyle D}$

${\displaystyle k={\frac {f}{D}}}$

the f-number are. The size of the diffraction disk is proportional to the f-number.

To calculate the spherical aberration, rays of light can be considered that correspond to the height of incidence

${\displaystyle H={\frac {D}{2}}={\frac {f}{2\cdot k}}}$

fall parallel to the optical axis on the flat lens surface facing the object. These are not broken when entering the optically denser medium of the lens material with the refractive index , since they strike perpendicularly . On the image side, these rays form the angle to the surface perpendicular of the lens in the lens and outside the lens the angle and are refracted according to Snell's law of refraction . The following applies: ${\displaystyle n}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$

${\displaystyle \sin(\alpha )={\frac {H}{R}}}$, so ${\displaystyle \alpha =\arcsin \left({\frac {H}{R}}\right)=\arcsin \left({\frac {f}{2\cdot k\cdot R}}\right)}$

and

${\displaystyle \sin(\beta )=n\cdot {\frac {H}{R}}}$, so ${\displaystyle \beta =\arcsin \left(n\cdot {\frac {H}{R}}\right)=\arcsin \left({\frac {n\cdot f}{2\cdot k\cdot R}}\right)}$

These rays then intersect the optical axis at the angle . The image-side focal distance , measured from the apex of the lens is then obtained as a function of the incidence height by means of the sine theorem to: ${\displaystyle \beta -\alpha }$ ${\displaystyle x}$ ${\displaystyle H}$

${\displaystyle x(H)={\frac {n\cdot H}{\sin(\beta -\alpha )}}-R}$

For rays close to the axis , this relationship is simplified by forming the limit value with : ${\displaystyle H\rightarrow 0}$

${\displaystyle x(0)=f=R\cdot \left({\frac {n}{n-1}}-1\right)}$

the focal length and the back focal length of the lens are then identical. ${\displaystyle f}$ ${\displaystyle x(0)}$

Using the f-number and the focal length, the focal length results in:

${\displaystyle x(k)={\frac {n\cdot f}{2\cdot k\cdot \sin(\beta -\alpha )}}-R}$

Circle of confusion with the diameter in an optical imaging with a plano-convex, spherical lens with the focal length due to spherical aberration with the focal length ${\displaystyle Z}$ ${\displaystyle f}$ ${\displaystyle x}$

Due to the spherical aberration, the point of intersection of the rays refracted behind the lens with the optical axis moves closer to the lens, the greater the height of incidence . In the focal plane at a distance from the apex of the lens, there is no longer a point-like image, but a circle of confusion with the diameter: ${\displaystyle H}$ ${\displaystyle f}$

${\displaystyle Z=2\cdot (f-x)\cdot \tan(\beta -\alpha )}$

Sample calculation

With a refractive index of 1.50 and a radius of curvature of 100 millimeters, the result is a focal length of 200 millimeters. ${\displaystyle n}$ ${\displaystyle R}$ ${\displaystyle f}$

At a green wavelength of 550 nanometers (nm), the diameter of the diffraction disk is: ${\displaystyle \lambda }$

${\displaystyle d=2,44\cdot {550nm}\cdot k={1,342\mu m}\cdot k}$

The following table gives the entrance pupils and the diameters for the diffraction disk and for the circle of confusion for different f-stops (see diagram on the right): ${\displaystyle D}$ ${\displaystyle d}$ ${\displaystyle Z}$

Critical aperture at the intersection of the two curves, which represent the blurring due to the diffraction disk with the diameter (red) and the circle of confusion due to the aperture error with the diameter (blue) logarithmically above the f-number . ${\displaystyle d}$ ${\displaystyle Z}$ ${\displaystyle k}$

F-number ${\displaystyle k}$	Entry pupil in mm ${\displaystyle D}$	Angle in ° ${\displaystyle \alpha }$	Angle in ° ${\displaystyle \beta }$	Diameter Airy disk in microns ${\displaystyle d}$	Diameter of the circle of confusion in µm ${\displaystyle Z}$
2.0	100.0	30.0	48.6	3	43553
2.8	70.7	20.7	32.0	4th	11970
4.0	50.0	14.5	22.0	5	3835
5.7	35.4	10.2	15.4	8th	1297
8.0	25.0	7.2	10.8	11	449
11.3	17.7	5.1	7.6	15th	157
16.0	12.5	3.6	5.4	21st	55
22.6	8.8	2.5	3.8	30th	19th
32.0	6.3	1.8	2.7	43	7th

The f-number of the critical aperture in this optical imaging is f / 26.7 (assumption: linear addition). In the example given, this corresponds to an aperture D of 7.5 millimeters. The diameter of the diffraction disk is 36.4 micrometers (µm), the circle of confusion is 11.4 µm. The total is 47.8 µm. The minimum is not at the intersection of the functions (the sum is about 55 µm there).

literature

• Karl Kraus: Photogrammetry. Volume 1: Geometric information from photographs and laser scanner recordings. 7th, fully revised and expanded edition. Walter de Gruyter, Berlin a. a. 2004, ISBN 3-11-017708-0 , p. 68.
• Günter Olberg: Scientific animal photography. German Science Publishing House, Berlin 1960.

Individual evidence

1. ↑ Hermann Slevogt: Technische Optik , p. 126, Walter de Gruyter, 1974, ISBN 9783110842432 , accessed on February 14, 2017