Steiner tree problem

The Steiner tree problem , one after Swiss mathematician Jakob Steiner called mathematical problem is a generalization of the problem of the minimum spanning tree . Here, as there, the shortest graph is sought which connects a finite number of given points (the terminals ) and which in this way forms the shortest route network between these points. With the problem of the minimal spanning tree, this graph is only spanned between the terminals, with the Steiner tree problem, on the other hand, one can add a finite number of further points (the Steiner points ) to the starting points from a likewise given set (the non-terminals ) , which then serve as additional branches in the route network, in order to shorten this further. As with the minimal spanning tree, the result is a tree . The theoretical and practical difficulty in solving the Steiner tree problem is to make an appropriate selection of the Steiner points.

The calculation of Steiner trees finds practical application in the planning of path and telecommunication networks and the design of integrated circuits .

example

Minimal spanning tree (blue) and Steiner tree (red)

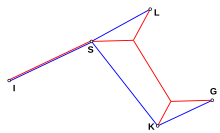
The adjacent drawing shows five points that represent the mutual location of the airports in Central Austria. If you set yourself the task of connecting all these places with a network of minimum total length of airlines, the result is the network drawn in blue, the minimum spanning tree. If, however, a motorway network of minimal length is involved, you can further reduce the network by creating two motorway triangles and the result is the network drawn in red, the Steiner tree.

In this example the five airports are the terminals, all other points on the level are the non-terminals and the two motorway triangles are the Steiner points. The distances are those from Euclidean geometry . Such Steiner tree problems are therefore called "Euclidean" or "geometric", because the solution is found with the help of geometric properties of the Steiner points. Below is an example of a graph-theoretical or discrete Steiner tree problem.

definition

In the following two different mathematical specifications of the Steiner tree problem are given. They are not equivalent; the differences are discussed below.

Requirements (general variant): A set is given on which a metric is defined. Let further be the set of so-called terminals, a finite subset of . ${\displaystyle V}$ ${\displaystyle T}$ ${\displaystyle V}$

If finite, it forms an edge-weighted graph with the distances , and the Steiner tree problem can be understood as a purely graph-theoretic problem: From the graph of all points in , the terminal as well as the nonterminal, a subgraph is determined that contains at least the terminals. The last paragraph then has the following form: ${\displaystyle V}$ ${\displaystyle V}$

Requirements (graph variant): Let be a connected , undirected graph without multiple edges , where is the node set and the edge set. Furthermore, let the set of so-called terminals be a subset of . Furthermore, a function is given that assigns a positive real value, its weight, to each edge , i.e. it is an edge-weighted graph . ${\displaystyle G=(V,E)}$ ${\displaystyle V}$ ${\displaystyle E}$ ${\displaystyle T}$ ${\displaystyle V}$ ${\displaystyle E}$ ${\displaystyle G}$

Problem: Based on one of the two prerequisites, a graph is now sought that connects all nodes and in which the sum of the distances or edge weights is minimal. If necessary, nodes from can also be used; these nodes are then Steiner node or Steiner points mentioned. It is easy to see that the graph is a tree . This is called the Steiner Tree . There can be several minimal such trees for a given task, i.e. several Steiner trees, in some metrics even none or an infinite number. ${\displaystyle T}$ ${\displaystyle V\setminus T}$

Usually the word "Steinerbaum" is used for such a minimal tree; the expression “minimal Steiner tree” is then pleonastic . Occasionally, however, one also finds “Steinerbaum” as a name for a tree whose structure makes it a possible solution, and one looks for the minimal ones among these. The term “Steinerbaum” should therefore always be defined to avoid confusion.

The second variant only fits finite ones . Even then, the two definitions are not exactly equivalent: ${\displaystyle V}$

• The graph in the graph variant will usually contain pairs of nodes between which there is no edge. This would correspond to an infinite distance in the metric; a metric is always real. In practice this doesn't matter: you can assign weights to the non-existent edges that are greater than the sum of all edge weights in ; such edges cannot appear in the Steiner tree. ${\displaystyle G}$ ${\displaystyle G}$
• The triangle inequality is not required in the graph variant. This means that the case may arise that a direct edge has to be replaced by a detour via one or more Steiner points in order to minimize the graph; this is especially the case with the edges that do not exist in. ${\displaystyle G}$

These non-metric cases of edge weights in the graph can, however, be reduced to the metric case. To do this, a complete graph is formed with edge weights that form a metric, namely the weight of the edge from to is defined as the length (i.e. the sum of the edge weights) of a shortest path from to in . Then you solve the Steiner tree problem. If edges occur in the Steiner tree that have a lower edge weight than in , they are replaced by a shortest path in ; the total length of the Steiner tree does not change and one gets a solution to the original non-metric problem in . ${\displaystyle G}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle G}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle G}$ ${\displaystyle G}$ ${\displaystyle G}$

Euclidean Steiner Tree Problem

As an example of a Steiner tree problem in a metric space with an infinite (even uncountable) number of points, the Euclidean Steiner tree problem is mentioned here, i.e. the finding of a minimal network of paths between a finite number of points in the plane. The example at the beginning of the article is Euclidean. Euclidean Steiner tree problems are the most vivid and therefore the first to be explored historically. The simplest nontrivial case, the Steiner tree for three points in the plane, has been solved by Torricelli since the 17th century : If every angle of the triangle formed is less than 120 °, the first Fermat point of the triangle is the only Steiner point and the Steiner tree exists from the three connecting lines from there to the three corners of the triangle ( proof here ). If, on the other hand, an angle is greater than or equal to 120 °, the Steiner tree is formed by its two legs. In both cases, the Steiner tree of the triangle does not contain an angle smaller than 120 °. This results in a number of properties of the Steiner tree:

1. Nowhere in the Steiner tree can an angle between edges occur that is smaller than 120 °, regardless of whether the vertex is a terminal or a Steiner point. Otherwise, one could replace the legs of the angle with the Steiner tree of the triangle formed by the angle and thus replace the Steiner tree with a shorter graph.
2. Exactly three edges always start from the Steiner points, between which there are 120 ° angles. A Steiner point between fewer than three edges could be omitted without lengthening the Steiner tree, and with more than three edges point 1 would be violated.
3. If all terminals are leaves of the Steiner tree (this is called a full Steiner tree ), there are exactly Steiner points, otherwise fewer than . This follows directly from point 2. ${\displaystyle n}$ ${\displaystyle n-2}$ ${\displaystyle n-2}$
4. Each Steiner tree can be clearly broken down into edge-disjoint full Steiner trees; Terminals that are not leaves of the Steiner tree belong to as many components as there are edges, i.e. to two or three.

In the example at the beginning of the article, the angle is greater than 120 °, the others equal 120 °. Three edges each start from the Steiner points. The point is not a leaf of the Steiner tree; therefore the Steiner tree has less than 5–2 = 3 Steiner points, namely only 2. The Steiner tree can be broken down into the two full Steiner trees with the terminal quantities and . ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle \left\{I,S\right\}}$ ${\displaystyle \left\{L,S,K,G\right\}}$

The mentioned properties of Steiner trees are necessary, but not sufficient. A tree with leaves and interior points of degree 3 and angles of 120 ° between the edges is not necessarily of minimum length, nor is a union of Steiner trees necessary for the entire terminal set, even if condition 1 is met at the interface. ${\displaystyle n}$ ${\displaystyle n-2}$

The construction of the Fermat point can be iteratively expanded to more than three points. However, although it generally leads to locally minimal trees (i.e. the tree does not get shorter when a single Steiner point is not moved ), one can only arrive at a global minimum if one tried all of the very numerous possibilities that are presented at each step surrender.

Graph theoretical Steiner tree problem

example

Map of the rail network of the imaginary state. Large cities are shown in red, small towns in black.

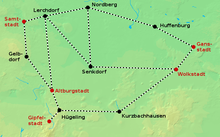
A state wants to modernize its ailing rail network so that it can be operated with electric locomotives . For this purpose, the existing tracks are to be provided with overhead lines; new tracks should not be laid. However, the budget is not enough to electrify the entire network, which is why the government decides to electrify only so many routes that it is possible to drive from every big city with an electric locomotive to every other big city (this does not exclude that the electric locomotive also drives through small towns). At the same time, the total costs for the modernization should be kept as low as possible. For the sake of simplicity, this example assumes that the costs of modernization depend only on the length of the route, not on the nature of the terrain, etc.

Graph presentation of the rail network. The numbers stand for route lengths in km. The Steiner tree is marked in red.

In terms of graph theory, the route network can be viewed as a graph in which the nodes represent cities and the edges represent existing railway lines between the cities. Each edge is assigned a numerical value (its weight) that corresponds to the length of the route. The cities to be connected can now be understood as terminals. The task is thus to find a weight-minimal subset of the edges that connect all terminals; In other words: to find an overhead line network that connects all major cities and is as inexpensive as possible. The search for this subset corresponds to the search for a Steiner tree.

The Steinerbaum pictured on the right represents all the routes that have to be electrified to connect all major cities. In this example, 190 km of overhead lines are required for this; the objective cannot be achieved with less management.

While it is still relatively easy to find the Steiner Tree in this example, for larger rail networks with more cities it is practically impossible for computers as well as for people to find an optimal solution.

Complexity of the general problem

The graph-theoretical Steiner tree problem belongs to the list of 21 classical NP-complete problems , of which Richard Karp was able to show in 1972 that they belong to this class. Since the Steiner tree problem is NP-complete , according to the current state of knowledge it is hopeless to always optimally solve problems of any size in a reasonable time. For this reason, it makes sense to investigate methods which, through approximation , deliver a perhaps not optimal, but nevertheless “good” solution for a given Steiner tree problem.

Approximability

With the help of an enumeration algorithm, the calculation of a minimal Steiner tree in polynomial time is possible if the number of non-terminals is limited, i.e. H. if one restricts oneself to instances in which no more than k non-terminals are contained for a given k . A special case here is k = 0, which is identical to the search for a minimal spanning tree.

The Dreyfus-Wagner algorithm delivers a minimal Steiner tree in polynomial time if the number of terminals is logarithmically restricted in the size of the graph, i.e. H. if you limit yourself to instances in which no more than terminals are included for a given constant . A special case here is | T | = 2, which is the same as finding a shortest path. ${\displaystyle c}$ ${\displaystyle c\cdot \log(|V|)}$

If P is not equal to NP (see P-NP problem ), there are also no polynomial algorithms that provide arbitrarily good approximate solutions ( PAS ).

The combinatorial approximation algorithms with the best known approximation quality are the relative greedy algorithm (approximation quality ) and the loss-contraction algorithm (approximation quality ). It is assumed for both algorithms that their analysis has not yet been optimally possible. In this respect it is not clear whether the relative greedy algorithm does not approximate better than the loss-contraction algorithm. Both algorithms try to approximate so-called k-Steiner trees. An LP -based algorithm achieves a better approximation quality of . All the algorithms mentioned are approximation schemes, that is to say a set of algorithms that achieve the quality of approximation mentioned for each arbitrarily small one . However, their runtime increases very sharply with falling and is therefore useless for real applications. A polynomial time algorithm with approximation quality 1.25 is known to limit the problem to distances 1 and 2. ${\displaystyle 1+\ln 2+\varepsilon <1{,}694}$ ${\displaystyle 1+\ln(3/2)+\varepsilon <1{,}550}$ ${\displaystyle \ln(4)+\varepsilon <1{,}39}$ ${\displaystyle \varepsilon >0}$ ${\displaystyle \varepsilon }$

More efficient approximation algorithms

The algorithm by Kou, Markowsky and Berman achieves approximation quality 2 and with running time O (| V | ² · log | V | + | V | · | E |) is significantly faster than the relative greedy algorithm or the loss-contraction algorithm . To do this, he calculates a distance graph and then a minimal spanning tree. The calculation of the distance graph essentially determines the running time of the algorithm. Mehlhorn's algorithm improves this running time to O (| V | · log | V | + | E |) by calculating only one modified distance graph instead of a complete one. Mehlhorn's algorithm also achieves approximation quality 2. The analysis of the Kou-Markowsky-Berman and Mehlhorn algorithms is as good as possible.

Complexity of special variants

As with many other difficult problems in theoretical computer science, there are also numerous limiting variants for the Steiner tree problem. Here one tries to drastically reduce the search space of the problem through restrictions and constraints and thus to greatly accelerate the calculation of a solution.

However, the Steiner tree problem remains NP-complete if one restricts oneself to bipartite unweighted graphs. Even with the restriction to metric graphs , the problem remains NP-complete.

Often the metric Steiner tree problem is also generalized in such a way that the set of nodes is infinite, for example, in many problems, the plane is viewed as a set of nodes. The nodes are then connected in pairs by an edge according to the metric used. Only the number of terminals then remains finite. Polynomial approximation schemes exist for Euclidean metrics or the Manhattan metrics , which are given relatively frequently in practical applications , so that good solutions to the problem can be found even for several thousand nodes. While the Steiner tree problem for the Manhattan metric can be reduced to the Steiner tree problem in graphs with the Hanan lattice, it is not known for the Steiner tree problem in the Euclidean metric whether it is NP-complete, since it belongs to the complexity class NP is unknown.

See also

• Chip design
• Floor planning

Individual evidence

1. ↑ See e.g. E.g .: Chiang, C., Sarrafzadeh, M., Wong, CK Global routing based on Steiner min-max trees . In: IEEE Transactions on Computer-Aided Design . Vol. 9, No. 12, 1990. ISSN  0278-0070
2. ↑ Clemens Gröpl, Stefan Hougardy, Till Nierhoff, Hans Jürgen Prömel . Lower Bounds for Approximation Algorithms for the Steiner Tree Problem . In: Lecture Notes in Computer Science . Vol. 2204/2001. Springer, ISSN  0302-9743 , p. 217. ( PS; 239 KB )
3. ↑ G. Robins, A. Zelikovsky. Improved Steiner tree approximation in graphs . In: Proceedings of the Eleventh Annual ACM-SIAM Symposium on Discrete Algorithms . SODA 2000, 770-779 ( PDF; 260 KB )
4. ↑ Michel X. Goemans , Neil Olver, Thomas Rothvoss , Rico Zenklusen: Matroids and Integrality Gaps for Hypergraphic Steiner Tree Relaxations . In: Proceedings of the 44th Symposium on Theory of Computing . STOC 2012, 1161-1176
5. ^ Piotr Berman, Marek Karpinski, Alexander Zelikovsky (2009). "1.25 Approximation Algorithm for Steiner Tree Problem with Distances 1 and 2". Lecture Notes in Computer Science 5664 : 86-97; doi : 10.1007 / 978-3-642-03367-4_8
6. ↑ Kurt Mehlhorn . A Faster Approximation Algorithm for the Steiner Problem in Graphs. Information Processing Letters, 27 (2): 125-128, 1988.
7. ↑ M. Hanan, On Steiner's problem with rectilinear distance, J. SIAM Appl. Math. 14 (1966), 255-265.

literature

• Hans Jürgen Prömel, Angelika Steger. The Steiner Tree Problem. A Tour through Graphs, Algorithms, and Complexity , Vieweg 2002, ISBN 3-528-06762-4 .

Web links

• An open source computer program in C for the "exact" calculation of minimal Euclidean Steiner trees
• Lecture on the subject by Ronald L. Graham: The Shortest Network Problem (1988)