Subset

Venn diagram : A is a (real) subset of B .

The mathematical terms subset and superset describe a relationship between two sets . Another word for subset is subset .

For the mathematical representation of the embedding of a subset to its basic amount mathematical function of the subset relationship that is inclusion mapping used. is a subset of and is a superset of if every element of is also contained in. If also contains further elements that are not contained in, then is a true subset of and is a true superset of . The set of all subsets of a given set is called the power set of . ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle A}$

Georg Cantor - the "inventor" of set theory - coined the term subset from 1884; the symbol of the subset relation was introduced by Ernst Schröder in 1890 in his " Algebra of Logic ".

definition

If and are sets and every element of is also an element of , one calls a subset or subset of : ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle A\subseteq B:\Longleftrightarrow \forall x\in A\colon x\in B}$

Conversely, the superset of is called if and only if is a subset of : ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle B\supseteq A:\Longleftrightarrow A\subseteq B}$

There is also the concept of the real subset. is a proper subset of if and only if a subset of and is not identical to . ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle A\subsetneq B:\Longleftrightarrow A\subseteq B\land A\neq B}$

Again you write when . ${\displaystyle B\supsetneq A}$ ${\displaystyle A\subsetneq B}$

Further notations

⊂⊊⊆⊇⊋⊃

Some authors also use the characters and for subset and superset instead of and . Most of the time, the author does not define the term “real subset”. ${\displaystyle \subset }$ ${\displaystyle \supset }$ ${\displaystyle \subseteq }$ ${\displaystyle \supseteq }$

Other authors prefer the characters and instead of and for proper subset and superset . This usage is fittingly reminiscent of the signs of inequality and . Since this notation is mostly used when the difference between real and non-real subset is important, the characters and are rarely used. ${\displaystyle \subset }$ ${\displaystyle \supset }$ ${\displaystyle \subsetneq }$ ${\displaystyle \supsetneq }$ ${\displaystyle \leq }$ ${\displaystyle <}$ ${\displaystyle \subsetneq }$ ${\displaystyle \supsetneq }$

Variants of the character are also , and . If is not a subset of , can also be used. Corresponding spellings are for , and for , as well as (no superset). ${\displaystyle \subsetneq }$ ${\displaystyle \varsubsetneq }$ ${\displaystyle \subsetneqq }$ ${\displaystyle \varsubsetneqq }$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A\nsubseteq B:\Longleftrightarrow \lnot \left(A\subseteq B\right)}$ ${\displaystyle \varsupsetneq }$ ${\displaystyle \supsetneq }$ ${\displaystyle \supsetneqq }$ ${\displaystyle \varsupsetneqq }$ ${\displaystyle \supsetneq }$ ${\displaystyle A\nsupseteq B}$

The corresponding Unicode symbols are: ⊂, ⊃, ⊆, ⊇, ⊄, ⊅, ⊈, ⊉, ⊊, ⊋ (see: Unicode Block Mathematical Operators ).

Ways of speaking

Instead of “ is a subset of .”, “The amount is contained in the amount ” or “The amount is comprised of .” Is also used . In the same way, instead of “ is a superset of .”, “The set contains the set .” Or “The set includes the set .” Is also used. If there cannot be misunderstandings, “ contains ” etc. is also said. Misunderstandings can arise especially with "The quantity contains the element ." ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$

Examples

The set {drum, playing card} is a subset of the set {guitar, playing card, digital camera, drum}

The regular polygons are a subset of the set of all polygons.

• {1, 2} is a (real) subset of {1, 2, 3}.
• {1, 2, 3} is a (spurious) subset of {1, 2, 3}.
• {1, 2, 3, 4} is not a subset of {1, 2, 3}.
• {1, 2, 3} is not a subset of {2, 3, 4}.
• {} is a (real) subset of {1, 2}.
• {1, 2, 3} is a (proper) superset of {1, 2}.
• {1, 2} is an (improper) superset of {1, 2}.
• {1} is not a superset of {1, 2}.
• The set of prime numbers is a real subset of the set of natural numbers .
• The set of rational numbers is a proper subset of the set of real numbers .

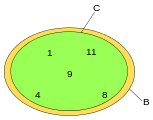
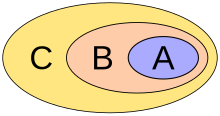
Further examples as quantity diagrams:

• 

  A is a proper subset of B

• 

  C is a subset of B, but not a real subset of B

properties

• The empty set is a subset of every set:

  ${\displaystyle \varnothing \subseteq A}$

• Every set is a subset of itself:

  ${\displaystyle A\subseteq A}$

• Characterization of inclusion with the help of the association :

  ${\displaystyle A\subseteq B\Leftrightarrow A\cup B=B}$

• Characterization of inclusion using the average :

  ${\displaystyle A\subseteq B\Leftrightarrow A\cap B=A}$

• Characterization of inclusion using the difference set :

  ${\displaystyle A\subseteq B\Leftrightarrow A\setminus B=\varnothing }$

• Characterization of inclusion using the characteristic function :

  ${\displaystyle A\subseteq B\Leftrightarrow \chi _{A}\leq \chi _{B}}$

• Two sets are equal if and only if each is a subset of the other:

  ${\displaystyle A=B\Leftrightarrow A\subseteq B\land B\subseteq A}$

  This rule is often used in proving the equality of two sets by showing mutual inclusion (in two steps).

• When transitioning to complement , the direction of inclusion reverses:

  ${\displaystyle A\subseteq B\Rightarrow A^{\rm {c}}\supseteq B^{\rm {c}}}$

• When forming the intersection, you always get a subset:

  ${\displaystyle A\cap B\subseteq A}$

• When forming the union one always gets a superset:

  ${\displaystyle A\cup B\supseteq A}$

Inclusion as an order relation

If A ⊆ B and B ⊆ C, then A ⊆ C too

Inclusion as a relation between sets fulfills the three properties of a partial order relation , namely it is reflexive , antisymmetric and transitive :

${\displaystyle A\subseteq A}$

${\displaystyle A\subseteq B\subseteq A\Rightarrow A=B}$

${\displaystyle A\subseteq B\subseteq C\Rightarrow A\subseteq C}$

(This is an abbreviation for and .) ${\displaystyle A\subseteq B\subseteq C}$ ${\displaystyle A\subseteq B}$ ${\displaystyle B\subseteq C}$

So if there is a set of sets (a set system ), then there is a partial order . This is especially true for the power set of a given set . ${\displaystyle M\,}$ ${\displaystyle (M,\subseteq )}$ ${\displaystyle {\mathcal {P}}(X)}$ ${\displaystyle X}$

Chains of inclusion

If a system of quantities is such that two of the quantities occurring in one encompass the other or are encompassed by the other, then such a system of quantities is called an inclusion chain . An example of this is provided by the system of left-hand unrestricted open intervals of . ${\displaystyle M\,}$ ${\displaystyle M\,}$ ${\displaystyle \{{]{-\infty ,x}[}\mid x\in \mathbb {R} \}}$ ${\displaystyle \mathbb {R} }$

A special case of an inclusion chain is when a (finite or infinite) sequence of quantities is given, which is arranged in ascending or descending order. You then write briefly: ${\displaystyle \subseteq }$ ${\displaystyle \supseteq }$

${\displaystyle A_{1}\subseteq A_{2}\subseteq A_{3}\subseteq \ ...}$

${\displaystyle A_{1}\supseteq A_{2}\supseteq A_{3}\supseteq \ ...}$

Size and number of subsets

• Every subset of a finite set is finite and the following applies to the cardinalities :

  ${\displaystyle A\subseteq B\Rightarrow \left|A\right|\leq \left|B\right|}$

  ${\displaystyle A\subsetneq B\Rightarrow \left|A\right|<\left|B\right|}$

• Every superset of an infinite set is infinite.
• Even with infinite quantities, the following applies to the thicknesses:

  ${\displaystyle A\subseteq B\Rightarrow \left|A\right|\leq \left|B\right|}$

• In the case of infinite sets, however, it is possible that a real subset has the same cardinality as its basic set. For example, the natural numbers are a true subset of the whole numbers , but the two sets are equally powerful (namely, countably infinite ).
• After Cantor's theorem is the power set of a quantity always more powerful than the amount itself: . ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle |A|<{\bigl |}{\mathcal {P}}(A){\bigr |}}$
• A finite set with elements has exactly subsets. ${\displaystyle n}$ ${\displaystyle 2^{n}}$
• The number of -element subsets of a -element (finite) set is given by the binomial coefficient . ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle {\tbinom {n}{k}}}$

See also

• characteristic function

literature

• Oliver Deiser: Introduction to set theory . Springer, 2004, ISBN 978-3-540-20401-5
• John L. Kelley: General Topology . Springer-Verlag, Berlin / Heidelberg / New York 1975, ISBN 3-540-90125-6 (reprint of the edition by Van Nostrand from 1955).

Web links

Wikibooks: Math for non-freaks: subset and real subset  - learning and teaching materials

Individual evidence

1. ↑ ^{a b} Oliver Deiser: Introduction to set theory . Springer, 2004, ISBN 978-3-540-20401-5 , p. 33 ( excerpt (Google) ).
2. ↑ Adolf Fraenkel: Introduction to set theory: An elementary introduction to the realm of the infinitely great . Springer, 2nd edition, 2013, ISBN 9783662259009 , p. 15
3. ↑ Set theory . In: Encyclopedia of Mathematics .
4. ↑ Otto Kerner, Joseph Maurer, Jutta Steffens, Thomas Thode, Rudolf Voller: Vieweg Mathematik Lexikon . Vieweg, 1988, ISBN 3-528-06308-4 , p. 190.