Terrestrial navigation
Terrestrial navigation is the term used to determine your position at sea with the help of terrestrial lines that are drawn on a nautical map (navigation with a compass and map in the field works according to the same principles ). A stationary line is a line on which the ship is at the time of observation, i.e. a geometric location in the sense of elementary geometry . At least two base lines are required to determine your position. The point of intersection of these stand lines is the so-called "observed ship location". This is entered on the nautical chart with a small circle around the intersection of the stand lines with the time. The base lines should intersect at an angle of 90 degrees if possible . The more the cutting angle deviates from 90 degrees, the less precise the location becomes. If more than two base lines can be found, then they generally form several points of intersection and these form a polygon (especially, for example, so-called "error triangle"). The desired ship's location is then assumed to be in the middle - more precisely: in the center of the area - of the polygon, unless considerations of systematic errors speak against it.
Terrestrial stand lines can be obtained with the following methods:
- 1. Bearing : Creates a baseline with a specific direction through the observed object. In a Mercator map , the constructed base line runs in a straight line.
- 2. Horizontal angle measurement : Creates an arc with a specific radius around the observed objects.
- 3. Distance determination : Creates a circular arc with a specific radius around the observed object.
- 4. Sounding : Generates an irregular depth line (can only be used if objective depth information - e.g. from the nautical chart - is available)
The 90 ° condition is ideally fulfilled with simultaneous bearing to and distance determination from one and the same object.
Bearings
Cross bearing
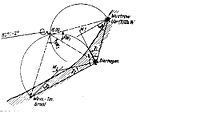
The cross bearing (also called "cutting backwards") is a simple method of determining position by bearing visible objects whose position is known. You need two observable points in the terrain of a known position , as well as a (bearing) compass , map, ruler and course triangle .
First, the direction to a prominent point in the area with a known position, here the ancient temple, is determined. The position of the boat is somewhere on the "bearing beam" with a directional angle of 354 ° , which is therefore also known as the base line. If possible at the same time, the directional angle to the second point on the site "factory chimney" is determined ( 55 ° ). The position of the boat is somewhere on the baseline with the direction angle 55 ° and on the baseline determined initially with the direction angle 354 ° , i.e. exactly at the intersection of the two baseline lines.
To avoid grinding cuts , the angle between the two bearings should not be less than 20 °. In order to reduce errors, further landmarks can be plotted, which results in further base lines and points of intersection that basically form an irregular polygon. The center of gravity of this polygon is regarded as the best possible mean ship location.
Methods other than sighting visible objects can also provide base lines for the cross bearing, e.g. B. radio direction finding and the targeting of acoustic signal generators with the help of directional microphones.
With the basic form of the cross bearing, the bearings must (if possible) take place simultaneously. However, once a bearing beam has been determined, it can also be used to determine the ship's location at a different point in time if it is known how far ("distance") the ship has meanwhile moved in which direction (" course ") on its course line. For this purpose, the bearing beam is shifted parallel in the direction of the course line by the distance covered in the meantime, and a position line is obtained for the new point in time. This procedure is called sailing of baseline lines.
See also: Cross bearing in aviation
Cross bearing
If you follow a known base line, for example with a bearing on the deck , you can determine your own position very precisely if another object is next to the base line and you are aiming at it "abeam", i.e. when it is exactly at right angles to the base line. The closer the object is to the baseline, the more precise the position found.
Sailing bearing
Even with a known position at only one point in the terrain, your own location can be determined by means of a bearing if you target it twice with a time delay and "see" it from different directions; however, the journey over the ground and the course over the ground must be known for the navigation bearing . Possibly. For this purpose, the journey over ground is calculated from the journey through the water and the current, and the course over ground is estimated from the course through the water, current offset and wind drift.
First of all, the direction to the distinctive “Ancient Temple” point in the area is determined. The position of the boat is also somewhere on the base line with the azimuth 354 °. The boat now continues for some time with a known course (95 °) on its yellow “course line” at a known speed, in the example 10 km. If it was on a base line with an angle of 354 ° at the time of the first bearing, it must now be on a base line shifted by 10 km towards 95 ° (in the example shown, it goes through the "fog bank"). To determine the location, the temple is now targeted again. The location of the boat is the intersection of this new stand line with an angle of 315 ° and the shifted ('sailed') stand line through the "fog bank" (angle 354 °).
With the geometric construction, the parallel shifting of the (first) bearing beam can be omitted if the distance between the ship and the object being sighted (ancient temple) is calculated using the sine law - all angles in the triangle and the sailed route are known.
If this triangle is isosceles in such a way that the sailed distance and the distance to the bearing object are of equal length, the calculation is unnecessary. Let α be the angle between the course line and a bearing ray, β that with respect to the other bearing. Then the triangle is isosceles if β = 180 ° - 2α; this condition then defines the time for the second bearing.
If the isosceles triangle is also right-angled, then α = β = 45 °. The name four-line bearing is also common for this special case of a navigation bearing ; because, expressed in the earlier angular unit, the nautical line , 45 ° = 4 lines.
However, in the special cases of seawater bearings that use the symmetry of an isosceles triangle, the small advantage of a slightly simpler construction is offset by the great disadvantage of a high observation effort.
Double horizontal angle measurement
To determine a position using horizontal angle measurement , two horizontal angles must first be measured:
- The angle α at which the distance between “temple” and “house” appears from the location
- The angle β at which the distance between “house” - “factory” appears from the location.
The angle measurement can take place directly with a suitable measuring device such as a sextant , or it can be calculated as the difference between bearings (using a compass) and the terrain points. When determining the angle using a compass, the horizontal angle measurement has the advantage over bearing that compass errors (caused by declination and magnetic interference ) generally do not falsify the position determination. The achievable accuracy is higher with the sextant.
The position you are looking for is on a circle on which all the places from which the route “Temple - House” appears at the angle α ( barrel circle ) are located. This circle can be constructed using the set of circumferential angles .
Your own position is also on the circle for the locations from which the distance “house - factory” appears at the angle β . However, there are two such circles in each case; only the relevant ones with the correct orientation for the angles α and β are shown in the picture . The position you are looking for lies at the intersection of those circles from which the terrain points appear in the “correct order”, i.e. the house to the right of the temple can be seen.
This method of determining the location fails if the three known points are all already on one of the circular base lines (circles in the picture), i.e. all four points are on a circle (in the drawing this would be the case, for example, if the factory was on the large red circle).
For all “normal cases”, the following “trial procedure” is a practicable and frequently used alternative to construction using compasses: If the measured horizontal angles are set on a double protractor with two adjustable legs, the desired location can be found by moving it on the map with the correct angle is the vertex common to both horizontal angles . This method can also be used if tracing paper with the drawn horizontal angles is used instead of the double protractor . This procedure corresponds to the reverse cut in geodesy .
There is also a construction method that works without a compass, the Pothenot construction.
Pothenot construction
Let three points (landmarks) be given. The position P (ship's location) is determined using two circles which intersect at point P. The two measured angles are plotted as angles 90 ° -alpha and angle 90 ° -beta from B over the legs AB and BD. Then the vertical is removed from A and C; the two extended lines intersect in D and E. Thus, two circles are determined by DAB and BCE, the intersection point P of which is the ship's location. From the DE line, the perpendicular to B is felled.
Bearing and Distance
To determine a location using this method, the following requirements must be met:
- The bearing to an object with a known position must be determined.
- The distance to the object must be known.
The position is then determined as follows:
A circle is drawn on the map with a compass around the known object at the same distance as you are. The bearing line is entered on the map crossing the object. Your own location is then at the point where the circle around the object crosses the bearing line.
The distance determination is generally carried out with an elevation angle measurement. The tangent is used here:
- With
- e = object distance
- h = known object height
- φ = measured elevation angle
Alternatively, an approximation for small angles is common, which can be carried out without a computer if necessary:
- (Nautical miles, angles in minutes)
A sextant is used to determine the altitude angle in seafaring. The height of the object must be known, for example the height of the fire carrier of a lighthouse, as specified in the lighthouse directory.
If the altitude is not known, the distance can still be determined according to the methods of the navigation bearing with the help of a second altitude angle measurement. Between the two measurements, the object to be tracked is approached in a straight line at a known speed and the time is measured in order to be able to calculate the distance covered (s = v ∙ t).
Bearing and sounding
To determine a location using this method, the following requirements must be met:
- The bearing of an object whose position is known must be determined
- The water depth at your own position must be known.
The position is then determined as follows:
The bearing line is entered crossing the object on the nautical chart. A map entry with the water depth must then be found on this line, which corresponds to the current water depth under the ship.
If no second baseline is available, you can also do a row plumbing, in which you plumb at fixed intervals, then transfer the measured depth values to a strip of (tracing) paper at the distances covered and then in the area of the coupled location - with orientation of the tracing paper in the direction of the map course - look for a point where the measured depth values roughly match the measured values. This method is only applicable when the seabed is changing fast enough to produce a noticeable change in depth values.
Great circle navigation serves the purpose of reaching the desired destination by the shortest possible route, whereby travel time and costs can generally also be saved. The shortest connection between the start and destination point on the earth's surface (so-called " orthodrome ") is on a great circle . In general, this connection is different from the line with a constant course angle (so-called " Loxodrome "), the difference can be significant over long distances. Orthodromes and loxodromes only coincide if the start and destination point are on the same meridian or the equator - i.e. already on a great circle. The great circle navigation simplifies the earth to an ideal spherical shape and offers several approximation methods to find the correct course angle for driving the shortest connection. For this purpose, the necessary loxodrome loads can be calculated at certain time intervals with the help of the expansion or determined from tables, or special maps with gnomonic projection are used.
The example clearly shows one of the aspects which are considered in the great circle navigation needs: Since the ( gyro -) compass always the geographic South Pole remains oriented towards, there are various points on the course line from Mount Vinson to a destination in Mac Robertson Country all different (compass) courses (170 °, 132 °, 13 °). Modern navigation computers can automatically make the necessary continuous adjustment of the course specification.
For navigation calculations with an accuracy of 1%, it is sufficient to set the earth as a sphere with a radius of R = 6,371 km. For small distances below 500 km, the difference between Orthodrome and Loxodrome is negligible.
Sailing baseline lines
If a position line is required at a different point in time than when it was determined, it is shifted in parallel by the distance covered in the meantime in the direction of the course that has meanwhile been driven. This construction is called sailing. It is used in the navigation bearing already dealt with above when an object is borne at different times.
literature
- H. Kärsten: Nautical paperback. Fachbuchverlag Leipzig, Chapter: I. Terrestrial Navigation pp. 13–71, various illustrations. 1955.
- Meldau-Steppes: Textbook of Navigation. Arthur Geist Verlag Bremen, Chapter: I. Terrestrial Navigation S.1.1-1.47 various Fig. 1958
- GDR author collective: Terrestrische Navigation , Verlag für Bautechnik 1968
- Winfried Boehm: Manual of the navigation. - Bussesche Verlagshandlung Herford, Chapters: 11 and 12 Terrest. Nav. Pp. 66–78 div. Figs. 1978. ISBN 3-87120-323-8
- Bernhard Berking, Werner Huth (ed.): Manual Nautics - Navigatorische Schiffsführung. Seehafen Verlag Hamburg, Chapter 2: Conventional Navigation, Sept. 2010. ISBN 978-3-87743-821-3