Topological sorting

In mathematics, topological sorting describes a sequence of things in which specified dependencies are fulfilled.

A person's upcoming activities, for example, are subject to a partial order : there are conditions such as “Activity A must be completed before activity B”. A sequence that fulfills all conditions is called a topological sorting of the set of pending activities. In contrast to the sorting of a total order, the order is not clear, but there can be several possibilities. When there are mutual dependencies, topological sorting is impossible.

From the point of view of set theory, topological sorting is a linear extension of a partial order . In 1930 Edward Szpilrajn showed that the axiom of choice implies that any partial order can be expanded to a linear order .

The topological sorting for finite sets (here the axiom of choice is not needed) is an important concept in many computer science applications . As early as 1961, Daniel J. Lasser developed an algorithm with which a topological sorting can be created in general. However, algorithms for special applications were previously known.

Furthermore, the topological sorting in graph theory plays a major role in the investigation of directed graphs for freedom from cycles.

The problem

Various objects can be clearly sorted according to measurable sizes, for example cities according to number of inhabitants, shoes according to shoe size, but also alphabetically according to name. However, this often no longer works if only relationships of the form predecessor / successor are specified and such relationships do not exist for every pair of objects. Mutual dependencies can also make sorting impossible (for example when playing chess: Anton wins against Bernd, Bernd wins against Clemens and Clemens wins against Anton). If it is possible to bring the objects into an order in which predecessors always appear before successors, then this order is a topological sorting of the objects.

Depending on the type of relationships, there can be none, only one or several different topological sortings. If there are mutual (cyclical) dependencies, topological sorting is not possible. In fact, one area of ​​application of topological sorting is checking whether there are cyclical dependencies.

Example: order of clothes to be put on

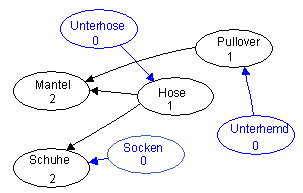
When putting on clothes, it is imperative that some parts are put on before others. A sweater must be put on before a coat. For example, if you have trousers, an undershirt, sweater, coat, socks, underpants and a pair of shoes, you can specify the following relationships for dressing.

• The undershirt in front of the sweater
• The underpants in front of the pants
• The sweater in front of the coat
• The pants in front of the coat
• The pants before the shoes
• The socks in front of the shoes

In order to determine a meaningful order, the seven items of clothing can be sorted topologically, for example

First the underpants, then the socks, pants, undershirt, sweater, coat, shoes.

But also

First the undershirt, then the underpants, then sweater, socks, pants, shoes, coat.

However not

First the sweater

because the undershirt has to be put on beforehand.

Mathematical description of the problem

The amount to be sorted

The objects to be sorted must be able to be partially arranged with regard to the relationship so that they can be sorted topologically. Mathematically, the objects form the elements of a set , the one with respect to relation (relation) has the following characteristics: ${\displaystyle M}$ ${\displaystyle R}$

The following applies to any elements of the set and the relation : ${\displaystyle a,b,c}$ ${\displaystyle M}$ ${\displaystyle R}$

1. Irreflectivity : ( not related to) ${\displaystyle \neg (a\,R\,a)}$ ${\displaystyle a}$ ${\displaystyle a}$
2. Transitivity : If and , then applies . ${\displaystyle a\,R\,b}$ ${\displaystyle b\,R\,c}$ ${\displaystyle a\,R\,c}$

Translated this means:

1. I can't put my pants on in front of my pants.
2. If I have to put on the undershirt before the sweater and the sweater before the coat, it follows that I have to put on the undershirt before the coat.

The set then forms a strict partial order with regard to the relation . Often you write instead of simply because the relation has similar properties as the smaller relation for numbers. (However, the smaller relation has some other properties that are not necessarily present here. For example, with the smaller relation of two different numbers, one can always decide which of the two is smaller. This is not required here. This would be in the example the comparison of socks and undershirt: you can't say that one of them has to be put on first.) ${\displaystyle M}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle <}$

Usually, however, not the entire relation is given, but only a sufficient subset of direct predecessor-successor pairs. The relation is then given via the transitive closure of the relation defined by the transferred pairs. For example, the complete relation for the example problem also states that the undershirt must be put on before the coat (because of "undershirt before sweater" and "sweater before coat", transitivity also means "undershirt before coat"). The transitive closure now consists in adding these pairs to the relation . However, when implementing a corresponding sorting algorithm, the complete relation is not explicitly generated. ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle R}$

The topologically sorted set

A certain sequence, on the other hand, is mathematically defined by a strict total order : For every two different elements off, it is determined whether it comes before or before (e.g. it is certain whether I put on my underpants first or my undershirt first this morning). The strict total order is thus mathematically defined by the additional axiom of ${\displaystyle a,b}$ ${\displaystyle M}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle b}$ ${\displaystyle a}$

• Trichotomy : For any element in either or or applies . ${\displaystyle a,b}$ ${\displaystyle M}$ ${\displaystyle a\,R\,b}$ ${\displaystyle a=b}$ ${\displaystyle b\,R\,a}$

The task of the topological sort is now to a given strict partial order is a total order to find, so for all with applies . ${\displaystyle R}$ ${\displaystyle {\tilde {R}}}$ ${\displaystyle a,b}$ ${\displaystyle a\,R\,b}$ ${\displaystyle a\,{\tilde {R}}\,b}$

Definition of the topological sorting

Motivated by the investigations in the two previous sections, one can now introduce the mathematical concept of a topological sorting:

Be a lot and . A set is called a topological sorting of for if and only if a strict total order is on and holds. ${\displaystyle M}$ ${\displaystyle R\subseteq M\times M}$ ${\displaystyle T\subseteq M\times M}$ ${\displaystyle M}$ ${\displaystyle R}$ ${\displaystyle T}$ ${\displaystyle M}$ ${\displaystyle R\subseteq T}$

This definition expressly does not restrict the concept of a topological sorting to finite sets, although such a restriction makes sense in connection with an algorithmic investigation.

Acyclic graphs and topological sorting

The already mentioned relationship between topological sorting and acyclic graphs can be summarized in the following sentence:

Be a lot and . Then are equivalent: ${\displaystyle M}$ ${\displaystyle R\subseteq M\times M}$

• There is a topological sort of for ${\displaystyle T}$ ${\displaystyle M}$ ${\displaystyle R}$
• ${\displaystyle (M,R)}$is an acyclic digraph

Representation as a directed graph

If you represent a relationship as an arrow between two elements, a directed graph is created . Such a directed graph has a topological sorting precisely when it is acyclic, i.e. there is no closed edge round trip.

The items of clothing can be sorted topologically by arranging them linearly and making sure that all arrows only point from left to right:

This gives a further characterization of a topological sorting that can also be used as a definition. A directed graph with nodes and edges amount , therefore a topological sort is a bijective map , the name of the node in a subset of the natural numbers (in other words, a one-to one-identification: Each node gets exactly one Number). It should apply here that is fulfilled for every edge . ${\displaystyle G}$ ${\displaystyle V,A}$ ${\displaystyle \Phi }$ ${\displaystyle a=(v,w)\in A\Rightarrow \Phi (v)<\Phi (w)}$

In the example one would have the figure

${\displaystyle \Phi \colon V\to \mathbb {N} .{\begin{cases}{\mbox{Unterhose}}&\mapsto 1\\{\mbox{Socke}}&\mapsto 2\\\dots \\{\mbox{Schuhe}}&\mapsto 7\end{cases}}}$

Such images are never clear. If you increase the image value node by node by any constant, you get another sorting with . If one restricts oneself to mapping into an element-wise smallest subset of natural numbers, the uniqueness depends on the graph structure. Directed paths can then be clearly sorted, "real" directed trees can have several sortings. ${\displaystyle \Phi '}$ ${\displaystyle \forall v\in V:\Phi '(v)=\Phi (v)+c,c\in \mathbb {N} }$

Sortable graphs

Graph 1

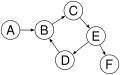
Graph 1 is topologically sortable. There are several solutions (for example ABCGDEF ). It does not matter that several elements exist without a predecessor (A and G), that some elements have several successors (for example, B has three successors) and some have several predecessors (D and E).

Graph 2

Graph 2 is also topologically sortable (for example ACBDE ), although it is not connected.

All graphs that do not contain any cycles (so-called acyclic graphs, see also tree ) can be sorted topologically.

Non-sortable graphs

• 

  Graph 3

• 

  Graph 4

• 

  Graph 5

Graph 3 is not topologically sortable because it contains a cycle, i.e. a mutual dependency (elements B, C, E and D).

Even if only two elements are mutually dependent, as in graph 4, a topological sorting is impossible. In general, exactly all graphs that contain a circle are not topologically sortable. Topological sortability is logically equivalent to acyclicity.

Graph 5 also has no topological sorting, not because it contains a “circle”, but because it violates the required irreflectivity. Node A is related to itself. Graph 5 is therefore a minimal, non-topologically sortable graph.

algorithm

Removal of elements without a predecessor

The algorithm assumes a directed graph. It removes elements without a predecessor from the graph until there are no more elements left.

First of all, all elements are given the previous number, i.e. the number of arrowheads that lead to the respective element:

Elements with a predecessor number 0 (marked in blue) have no other predecessors. They are removed from the graph. Here the socks, the underpants and the undershirt with the associated arrows can be removed. This also changes the previous numbers of other elements:

Removed elements:

Socks underpants undershirt

Now the sweater and pants have no predecessors, so they can be removed:

Removed elements:

Socks underpants undershirt pants sweater

Now only the coat and shoes remain, which are also removed. The topological sorting is finished when all elements could be removed:

Topological sorting:

Socks underpants undershirt pants sweater coat shoes

Representation in the computer

The objects (elements) themselves are usually placed in the

• Data structure of a list with object attributes (name, index, ...)

registered. To represent the relationships, an additional one is sufficient for each element

• List of references ( references or pointers ) to the successors of an object. The objects contain a reference to their respective successor list.

The sorting algorithm requires space for additional data that is described and used by the algorithm:

• For each object space for a number that contains the number of its predecessors.
• Optional an auxiliary list that includes objects without a predecessor.

Example:

For the dressing example above, the object list would e.g. B. looks like this:

1. trousers
2. coat
3. pullover
4. Shoes
5. Socks
6. Undershirt
7. Underpants

The successor lists would then look like this:

1. 2, 4
2. (empty list)
3. 2
4. (empty list)
5. 4th
6. 3
7. 1

The first list (for the pants) says that the coat (object 2) and shoes (object 4) can only be put on after the pants. The second list (for the coat) states that there is no such thing as an item of clothing that can only be put on after the coat.

The list of previous numbers has 7 elements (one per object), initially all entries are 0.

Topological sorting algorithm

Simple version with marking of elements

The sorting algorithm needs the information how many predecessors an element contains (number of predecessors). Elements already found must be removed from the list or marked. You can mark elements by setting the previous number to −1.

1. Calculate the previous number:

• Set the previous number of all elements to 0.
• For all elements go through the successor list and increase the previous number of each of these elements by 1.
  (Now all previous numbers are calculated)

In the example z. B. the pants (element 1) only have a predecessor (the underpants), so the 1 only appears once in the successor lists. The coat (element 2), however, has 2 predecessors (sweater and pants), which is why the 2 appears twice in the successor lists. Overall, the previous list thus results:

1. 1
2. 2
3. 1
4. 2
5. 0
6. 0
7. 0

2. As long as there are (unmarked) elements in the list:

• Search for an element with a previous number of 0.
  If no such element is found, a topological sorting is not possible because there are mutual dependencies (cycles). The algorithm breaks off with an error.
• Output the found element and remove it from the list or mark it (for example, set the previous number equal to -1 as a mark)
• Go through the list of successors of the element found and decrease the number of ancestors by 1. The element is now effectively removed from the element list. By reducing the number of predecessors, new elements can be created without a predecessor.

If all elements are output or marked, the topological sorting was successful.

In the example, element 5 (socks) is such an element without an ancestor. Therefore this element is output and marked with –1 (we could just as easily have started with element 6 or 7). The only successor objects to the socks are the shoes (element 4), so the number of previous elements of element 4 is reduced. After this step, the previous number list is

1. 1
2. 2
3. 1
4. 1
5. -1
6. 0
7. 0

and the previous edition is: socks

In the next step we find out that element 6 (undershirt) has no predecessors either. Again there is only one successor element, the sweater (number 3). So the previous number list after the second step is:

1. 1
2. 2
3. 0
4. 1
5. -1
6. -1
7. 0

and the output so far is: socks, undershirt

By reducing it by 1, the previous number of the sweater (element 3) became 0. So if we take the sweater next, we will only find element 2 (the coat) in its successor list, the previous number of which we therefore also have to reduce so that the List now

1. 1
2. 1
3. -1
4. 1
5. -1
6. -1
7. 0

is, and the previous edition: socks, undershirt, sweater .

Now, for the first time, we no longer have a choice about the next element: Only the underpants now have the previous number 0. Its removal then leads in the next step to a 0 for the pants (element 1), and its removal ultimately leads to both Element 2 (coat) and Element 4 (shoes) no longer have any predecessors. If we now choose the coat before the shoes, this results in the overall sorting

Socks, undershirt, sweater, underpants, pants, coat, shoes ,

which can easily be recognized as the correct topological sorting of these elements.

Extended version with an additional help list

An additional help list can be created to quickly find elements without a predecessor . After calculating the previous numbers, this is filled with all elements that were initially without an ancestor, i.e. with a previous number equal to zero. In phase 2, instead of searching for an element with a previous number of zero, one is simply taken from the auxiliary list. If the previous number of an element equals zero when decreasing by 1 during phase 2, it is added to the auxiliary list. The algorithm ends when there are no more elements in the auxiliary list. The marking can then also be dispensed with.

Time behavior (complexity)

The complexity of the algorithm describes the behavior over time with large amounts of data, more precisely the ratio of the execution times when the input data is enlarged. Does an algorithm need z. For example, for a set of data sets , the complexity is as the 10000 additional steps are no longer relevant for sufficiently large data sets , see Landau symbols . ${\displaystyle N}$ ${\displaystyle \vert N\vert ^{2}+10000}$ ${\displaystyle {\mathcal {O}}(\vert N\vert ^{2})}$

Average and worst case

For topological sorting with n elements and m relationships between them, the following applies to “normal” ( average case ) problems , since each element has only a constant number of relationships on average. In the extreme case ( worst case ), however, relationships can occur in a directed acyclic graph . ${\displaystyle {\mathcal {O}}(m)={\mathcal {O}}(n)}$ ${\displaystyle m=\sum _{i=1}^{n}(i-1)={\frac {n\cdot (n+1)}{2}}-n={\frac {n^{2}-n}{2}}={\mathcal {O}}(n^{2})}$

First phase: building up the previous numbers

The first phase sets the previous numbers to 0 and requires n loop passes ( ). It takes a time of the order of magnitude ( average case ) or ( worst case ) to run through the m successors . ${\displaystyle {\mathcal {O}}(n)}$ ${\displaystyle {\mathcal {O}}(n)}$ ${\displaystyle {\mathcal {O}}(n^{2})}$

Auxiliary list for items with no predecessor

Before the second phase, an auxiliary list is created that contains all elements without an ancestor ( ). After that, only new previous lots are inserted ( ) and removed ( ) from the auxiliary list . The search for unprecedented elements does not affect the time behavior. The same can be achieved by relocating unprecedented elements "forwards" (with possible). ${\displaystyle {\mathcal {O}}(n)}$ ${\displaystyle {\mathcal {O}}(1)}$ ${\displaystyle {\mathcal {O}}(1)}$ ${\displaystyle {\mathcal {O}}(1)}$

Second phase: removal of unprecedented elements

If successful, the second phase treats all n elements and reduces the average number of predecessors , so the time behavior is . ${\displaystyle {\frac {m}{n}}}$ ${\displaystyle {\mathcal {O}}(n)\cdot {\mathcal {O}}\left({\frac {m}{n}}\right)}$

Overall behavior

	Relationships m and objects n	Time behavior (with auxiliary list)
Average case	${\displaystyle {\mathcal {O}}(m)={\mathcal {O}}(n)}$	${\displaystyle {\mathcal {O}}(n)}$
Worst case	${\displaystyle {\mathcal {O}}(m)={\mathcal {O}}(n^{2})}$	${\displaystyle {\mathcal {O}}(n^{2})}$

Unfavorable structure of the lists

The algorithm in Niklaus Wirth's book (see literature) contains a reading phase in which he inserts the relationship pairs into a list, which in turn contains lists for the successors. It determines the respective successor list by means of a linear search ( ), which is carried out for each pair ( ) that is read in, i.e. all in all (quadratic). This worsens the overall timing. The lists could be built using a bucket sort algorithm , for example, but also in linear time . ${\displaystyle {\mathcal {O}}(n)}$ ${\displaystyle {\mathcal {O}}(m)}$ ${\displaystyle {\mathcal {O}}(n)\cdot {\mathcal {O}}(m)}$ ${\displaystyle {\mathcal {O}}(m)}$

Program in the Perl programming language

In the Perl programming language , lists can be implemented particularly easily with the help of dynamically growing fields (for example @Elemente). The specified program first reads relationship pairs of the form predecessor successor , each in a line and separated by spaces:

Katze Hund
Hahn Katze
Hund Esel

The output is

Hahn
Katze
Hund
Esel

When reading in the relationship pairs, a Perl hash is used to find the numerical index of existing elements. Elements without an index are created. For this purpose, a new index is assigned, the name is saved and an empty successor list is created. This list then includes the indices of the successor elements for the respective predecessors.

The algorithm only uses indices and runs as described above. The name saved under the index is not used again until the output.

The Perl script looks like this:

#!/usr/bin/perl
# Topologisches Sortierprogramm in Perl
# Lizenzstatus: GNU FDL, für Wikipedia
#
# =================================================================
# Unterprogramm zum Finden bzw. Neuanlegen eines Elements
# =================================================================
sub finde_oder_erzeuge_element
{       my ($str)=@_;
        my ($idx)=$hashindex{$str};
        if (!defined($idx)) { # Neues Element ...
                $idx=$objektzahl++;
                $hashindex{$str}=$idx;
                $name[$idx]=$str;
            @{$nachfolgerliste[$idx]}=();
        }
        return $idx;
}
# =================================================================
# Einlesen, Aufbau der Elementliste und der Nachfolgerlisten
# =================================================================
$objektzahl=0;
%hashindex=();
while (<>)
{       chomp;
        /^\s*(\S+)\s*(\S+)\s*$/ ||
          die "Bitte \"Vorgänger Nachfolger\" eingeben\n";
        ($vorgaenger,$nachfolger)=($1,$2);
        $v=finde_oder_erzeuge_element($vorgaenger);
        $n=finde_oder_erzeuge_element($nachfolger);
        push @{$nachfolgerliste[$v]},$n;
}
# =================================================================
# Topsort 1: Berechne Vorgängerzahlen
# =================================================================
for $n (0..$objektzahl-1) {
        $vorgaengerzahl[$n]=0;
}
for $v (0..$objektzahl-1) {
        for $n (@{$nachfolgerliste[$v]}) {
                ++$vorgaengerzahl[$n];
        }
}
# =================================================================
# Erzeuge die Hilfsliste für die Elemente mit Vorgängerzahl 0
# =================================================================
@hilfsliste=();
for $n (0..$objektzahl-1) {
        push(@hilfsliste,$n) if ($vorgaengerzahl[$n]==0)
}
# =================================================================
# Topsort 2: Gib solange möglich ein Element der Hilfsliste aus
#            Verringere Vorgängerzahl der Nachfolger des Elements
#            Neue Elemente mit Vorgängerzahl 0 in die Hilfsliste
# =================================================================
$ausgabe=0;
while (defined($v=pop(@hilfsliste))) {
        print "$name[$v]\n";
        ++$ausgabe;
        for $n (@{$nachfolgerliste[$v]}) {
                --$vorgaengerzahl[$n];
                push(@hilfsliste,$n) if ($vorgaengerzahl[$n]==0);
        }
}
die "Zyklen gefunden\n" if $ausgabe<$objektzahl;

Examples

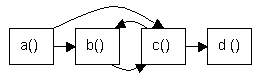
Subroutine calls and recursion

In computer programs , sub- programs can call further sub- programs . If no reciprocal calls or self-calls occur, a totally ordered sequence can be determined with the help of the topological sorting. Otherwise subroutines call each other recursively .

Subroutines with recursion	Subroutines without recursion
Prozedur a() { Aufruf von b() Aufruf von c() } Prozedur b() { Aufruf von c() } Prozedur c() { Aufruf von b() Aufruf von d() }	Prozedur a() { Aufruf von b() Aufruf von c() } Prozedur b() { Aufruf von d() } Prozedur c() { Aufruf von b() Aufruf von d() }
Not because procedure possible topological sorting b the procedure c calls and procedure c the procedure b (cycle).	Topological sorting: acbd

Main categories and sub-categories

Some category systems are arranged hierarchically. The top level contains the main categories, which in turn contain sub-categories. Subcategories can contain further subcategories to any depth. Usually you add a new category to an existing one when the number of objects in a category exceeds a certain limit. Other existing categories will be moved to the new category as appropriate. A superordinate category or a category from another main category can inadvertently be assigned to the new category, creating mutual dependencies and destroying the hierarchy of the system. A user who navigates through the (supposed) category tree can under certain circumstances go around forever "in circles", which the required hierarchy should prevent.

By topological sorting of the category tree one can prove that there are no cycles. All main categories are first classified in a hypothetical root tree. The relationship is the condition that one category is a direct sub-category of another category; this information is available anyway. If the topological sorting algorithm fails, there are cyclical dependencies and the system is no longer hierarchical.

tsort command under Unix and Linux

Unix- like operating systems often have a program called tsort that does a topological sorting. It used to be necessary to insert translated object files that are dependent on one another in the correct order in a program library , but it can also be used for other purposes:

$ tsort <<Ende
> Unterhemd Pullover
> Unterhose Hose
> Pullover Mantel
> Hose Mantel
> Hose Schuhe
> Socken Schuhe
> Ende
Socken
Unterhemd
Unterhose
Pullover
Hose
Schuhe
Mantel

Input are the dependencies in the form before after . The output is a topological sorting of the elements.

See also

• Cutting rule
• Gentzenscher's law
• Plank calculus
• Application example for topological sorting: Determining the insertion order for tables with referential integrity

literature

• Thomas Ottmann, Peter Widmayer: Algorithms and Data Structures . 4th edition. Spektrum Verlag, Heidelberg 2002, ISBN 3-8274-1029-0 .
• Niklaus Wirth : Algorithms and Data Structures, Pascal Version . 4th edition. Teubner Verlag, Stuttgart 1995, ISBN 3-519-12250-2 .
• Donald E. Knuth : The Art of Computer Programming . 3. Edition. tape 1 : Fundamental Algorithms. Addison-Wesley, 1997, ISBN 0-201-89683-4 .
• Edward Szpilrajn : Sur l'extension de l'ordre partiel . In: Fundamenta Mathematicae . tape 16 , 1930, ISSN  0016-2736 , p. 386-389 .
• Daniel J. Lasser : Topological Ordering of a List of Randomly-Numbered Elements of a Network . In: Communications of the ACM . tape 4 , 1961, ISSN  0001-0782 , pp. 167-168 .
• AB Kahn : Topological Sorting of Large Networks . In: Communications of the ACM . 1962, ISSN  0001-0782 , p. 558-562 .

Web links

• Niklaus Wirth's implementation in Pascal

Individual evidence

1. ^ Edward Szpilrajn: Sur l'extension de l'ordre partiel . In: Fundamenta Mathematicae . 16, 1930, pp. 386-389.