Cantor-Bernstein-Schröder theorem

The Cantor-Bernstein-Schröder theorem, or equivalence theorem for short, is a set theory theorem about the cardinalities of two sets. It is named after the mathematicians Georg Cantor (who was the first to formulate it) and Felix Bernstein and Ernst Schröder (who published the evidence) and is also known in the literature as the Cantor-Bernstein-Schröderscher [equivalence] theorem, the Cantor-Bernstein theorem , Cantor-Bernstein equivalence theorem, Schröder-Bernstein theorem or similar. However, it has also been independently proven by Richard Dedekind .

The proposition says: If a set A is equal to a subset of a second set B and this second set B is equal to a subset of the first set A, then A and B are equal.

The Cantor-Bernstein-Schröder theorem is an important aid in proving the equality of two sets.

history

The equivalence theorem was formulated in 1887 by Georg Cantor, but was only proven in 1897 by 19-year-old Felix Bernstein in a seminar led by Georg Cantor and at about the same time independently of Ernst Schröder. In the same year Cantor communicated Bernstein's proof to Émile Borel at the first international mathematicians' congress in Zurich.

Cantor's first mention of the equivalence theorem, 1887

Cantor had given this equivalence theorem for the first time in his philosophical treatise Communications on the Doctrine of the Transfinite from 1887 (without proof). In his great work Contributions to the Justification of Transfinite Set Theory of 1895 Cantor set up this theorem again and deduced it from the comparability theorem for cardinal numbers . However, Cantor could not prove the comparability principle. According to Friedrich Moritz Hartogs ( On the Problem of Well-Order, 1915 ) it is equivalent to the axiom of choice (or the principle of selection or the principle of well-order).

Dedekind himself found the proof of the equivalence theorem (which was found in his estate) on July 11, 1887, but he did not publish it and did not inform Cantor about it.
Ernst Zermelo rediscovered Dedekind's proof and in 1908 gave a proof in his treatise Investigations on the Fundamentals of Set Theory I , referring to Dedekind's chain theory from Dedekind's book What are and what should numbers be? (1888) resorted to. Giuseppe Peano gave similar evidence, leading to a priority dispute with Zermelo. Both proofs were the result of a challenge from Henri Poincaré , who around 1905 asked for proofs that did not require full induction. Because of Poincaré's challenge, Julius König's proof was also published and further research was encouraged.

Ernst Schröder had published a proof sketch in 1896 (on two definitions of finiteness and G. Cantor's theorems) which, however, turned out to be false, as Alwin Reinhold Korselt had noted in 1911 (on a proof of the equivalence theorem) ; Schröder confirmed the error in his proof there.

In his dissertation Richard Dedekind in 1887 and Bernstein in 1898 showed that the theorem can also be proven without the axiom of choice (Bernstein's proof appeared first in Borels Leçons sur la théorie des fonctions and then again in Bernstein's treatise Investigations from Set Theory ).

There are numerous other proofs of the theorem.

A suitable name for the equivalence theorem would be Cantor-Dedekind's equivalence theorem or Cantor-Dedekind-Bernstein's equivalence theorem. In addition, Bernstein has pointed out that Cantor himself proposed the designation "equivalence theorem".

sentence

The Cantor-Bernstein-Schröder theorem reads:

Let a set be equal to a subset of a set , and be equal to a subset of . Then and are equal. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle B}$

Two sets are called equal if there is a bijective mapping between them. Expressed by the powers of and the theorem reads: ${\displaystyle A}$ ${\displaystyle B}$

Out and follows . ${\displaystyle |A|\leqq |B|}$ ${\displaystyle |B|\leqq |A|}$ ${\displaystyle |A|=|B|}$

It then applies if and are equal, and then applies if and only if is equal to a subset of , that is, if there is an injective mapping of in . Expressed in terms of the properties of functions, the theorem reads: ${\displaystyle |A|=|B|}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle |A|\leqq |B|}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$

Be and quantities with one injection and one injection . Then there is a bijection . ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle f\colon A\to B}$ ${\displaystyle g\colon B\to A}$ ${\displaystyle h\colon A\to B}$

Proof idea

An idea of ​​proof is given below.

Define the quantities:

${\displaystyle C_{0}:=A\setminus g(B)}$,

${\displaystyle C_{n+1}:=g(f(C_{n}))\quad {\mbox{ für }}n\geqq 0}$,

${\displaystyle C:=\bigcup _{n=0}^{\infty }C_{n}}$.

For each of then translate: ${\displaystyle x}$ ${\displaystyle A}$

${\displaystyle h(x):={\begin{cases}f(x),&\mathrm {falls} \ x\in C,\\g^{-1}(x),&\mathrm {falls} \ x\notin C.\end{cases}}}$

Since in the case that not is in need are there exists a unique element and is a well-defined mapping to . ${\displaystyle x}$ ${\displaystyle C}$ ${\displaystyle x}$ ${\displaystyle g(B)}$ ${\displaystyle g^{-1}(x)}$ ${\displaystyle h}$ ${\displaystyle A}$ ${\displaystyle B}$

One can now show that this function is the desired bijection. ${\displaystyle h\colon A\to B}$

Note that this definition of is not constructive; h., there is no procedure in place for any amount , and injections , in finally deciding many steps, whether from in or not. This can of course be possible for special quantities and images. ${\displaystyle h}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle x}$ ${\displaystyle A}$ ${\displaystyle C}$

A short and easily understandable proof can also be found in Erich Kamke's Göschen volume theory .

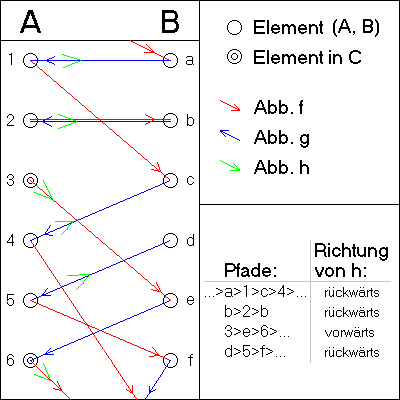
illustration

The definition of can be illustrated using the illustration opposite. ${\displaystyle h}$

Parts of the (disjoint) sets and as well as the figures and are shown . If one looks at the united as a graph , then the graph breaks down into different connected components. These can be divided into four types: ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle A}$ ${\displaystyle B}$

1. mutually infinite paths;
2. finite cycles;
3. infinite paths starting in; ${\displaystyle A}$
4. infinite paths that start in ${\displaystyle B}$

(One of each type is represented here, since the path through the element should be infinite on both sides). In general, however, it is not possible to decide in finitely many steps what type of path a given element is. ${\displaystyle a}$

The set defined in the Proof idea section now contains exactly those elements of which are part of a path beginning in. The mapping is defined in such a way that within each connected component it creates a bijection of the elements onto "neighboring" elements in the path (one has a choice of direction for the paths that are infinite on both sides and the finite cycles and one sets oneself to "backwards") ). ${\displaystyle C}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle h}$ ${\displaystyle A}$ ${\displaystyle B}$

generalization

The Cantor-Bernstein-Schröder theorem turns out to be a direct consequence of Banach's mapping theorem .

See also

• Comparability rate

literature

• Felix Bernstein: Investigations from set theory . Book printing of the orphanage, Halle a. S. 1901 ( Internet Archive - Inaugural dissertation with David Hilbert).
  • Felix Bernstein: Investigations from set theory . In: Felix Klein , Walther von Dyck , David Hilbert (Hrsg.): Mathematische Annalen . tape 61 , no. 1 . B. G. Teubner, 1905, ISSN  0025-5831 , p. 117–155 , doi : 10.1007 / BF01457734 ( gdz.sub.uni-goettingen.de [PDF] unchanged edition except for a few improvements and comments).
• Émile Borel: Leçons sur la théorie des fonctions . Gauthier-Villars et fils, Paris 1898, p. 103 ff . ( Text archive - Internet Archive ).
• Günter Bruns, Jürgen Schmidt: A tightening of the Bernstein equivalence theorem . In: Heinrich Behnke , Richard Courant , Heinz Hopf , Gottfried Köthe , Kurt Reidemeister , Bartel L. van der Waerden (eds.): Mathematische Annalen . tape 135 , no. 3 . Springer-Verlag, 1958, ISSN  0025-5831 , p. 257–262 , doi : 10.1007 / BF01351802 ( gdz.sub.uni-goettingen.de [PDF] received on January 3, 1958).
• Georg Cantor: Foundations of a general theory of manifolds . A mathematical-philosophical attempt in the doctrine of the infinite. Commissions-Verlag by B. G. Teubner, Leipzig 1883 ( digital.slub-dresden.de [PDF]).
  • Georg Cantor: About infinite, linear point manifolds . 5. In: Felix Klein, Adolph Mayer (Ed.): Math. Ann . tape 21 , no. 4 . B. G. Teubner, 1883, ISSN  0025-5831 , p. 545–591 , doi : 10.1007 / BF01446819 ( gdz.sub.uni-goettingen.de [PDF] reprint; Halle, October 1882).
• Georg Cantor: Collected treatises of mathematical and philosophical content . With explanatory notes and additions from the Cantor – Dedekind correspondence. Ed .: Adolf Fraenkel (curriculum vitae); Ernst Zermelo. Published by Julius Springer, Berlin 1932 ( gdz.sub.uni-goettingen.de ).
• Richard Dedekind: What are and what are the numbers? 2nd, unchanged edition. Friedrich Vieweg & Sohn, Braunschweig 1893 ( echo.mpiwg-berlin.mpg.de - first edition: 1888).
• Richard Dedekind: Collected mathematical works . Ed .: Robert Fricke , Emmy Noether , Øystein Ore . tape 3 . Friedr. Vieweg & Sohn, Braunschweig 1932 ( gdz.sub.uni-goettingen.de ).
• Friedrich Moritz Hartogs: About the problem of well-being . In: Felix Klein, Walther von Dyck, David Hilbert, Otto Blumenthal (eds.): Math. Ann . tape 76 , no. 4 . B. G. Teubner, 1915, ISSN  0025-5831 , p. 438–443 , doi : 10.1007 / BF01458215 ( gdz.sub.uni-goettingen.de [PDF] July 1914).
• Alwin Reinhold Korselt: About a proof of the equivalence theorem . In: Felix Klein, Walther von Dyck, David Hilbert, Otto Blumenthal (eds.): Math. Ann . tape 70 , no. 2 . B. G. Teubner, 1911, ISSN  0025-5831 , p. 294–296 , doi : 10.1007 / BF01461161 ( gdz.sub.uni-goettingen.de [PDF] end of April 1910).
• Ernst Schröder: About two definitions of finitude and G. Cantor's theorems . In: Imperial Leopoldino-Carolinische Deutsche Akademie der Naturforscher (ed.): Nova Acta, Abhandlungen der Kaiserl. Leop.-Carol. German Academy of Natural Scientists . tape 71 , no. 6 . Johann Ambrosius Barth Verlag, Halle a. P. 1898, p. 303-376 ( biodiversitylibrary.org - February 1896, received May 21, 1896).
• Ernst Zermelo: Investigations into the basics of set theory . I. In: Felix Klein, Walther von Dyck, David Hilbert, Otto Blumenthal (eds.): Math. Ann . tape 65 , no. 2 . B. G. Teubner, 1908, ISSN  0025-5831 , p. 261–281 , doi : 10.1007 / BF01449999 ( gdz.sub.uni-goettingen.de [PDF] July 30, 1907).
• Arie Hinkis: Proofs of the Cantor-Bernstein theorem, a mathematical excursion. Birkhäuser 2013.

Web links

• Martin_Infinite: Schröder-Bernstein's theorem. Explicitly. Matroids Matheplanet, November 19, 2005, accessed December 28, 2012 . 

Individual evidence

1. ↑ Oliver Deiser: Introduction to set theory . Georg Cantor's set theory and its axiomatization by Ernst Zermelo. 3rd, corrected edition. Springer-Verlag, Berlin / Heidelberg 2010, ISBN 3-540-20401-6 , pp. 71, 501 , doi : 10.1007 / 978-3-642-01445-1 ( limited preview in Google Book search).
2. ^ Patrick Suppes : Axiomatic Set Theory . 1st edition. Dover Publications, New York 1972, ISBN 0-486-61630-4 , pp. 95 f . ( limited preview in Google Book search).
3. ↑ ^{a b} Georg Cantor: mathematical Collected essays and philosophical content . With explanatory notes and additions from the Cantor – Dedekind correspondence. Ed .: Adolf Fraenkel [curriculum vitae], Ernst Zermelo. Published by Julius Springer, Berlin 1932, p. 378-439 , p. 413 there ( gdz.sub.uni-goettingen.de ).
4. ↑ Georg Cantor: Collected treatises of mathematical and philosophical content . With explanatory notes and additions from the Cantor – Dedekind correspondence. Ed .: Adolf Fraenkel [curriculum vitae], Ernst Zermelo. Published by Julius Springer, Berlin 1932, sentence B, p. 285 ( gdz.sub.uni-goettingen.de ).
5. ↑ Friedrich M. Hartogs: About the problem of well-being . In: Felix Klein, Walther von Dyck, David Hilbert, Otto Blumenthal (eds.): Math. Ann . tape 76 , no. 4 . B. G. Teubner, 1915, ISSN  0025-5831 , p. 438–443 , doi : 10.1007 / BF01458215 ( gdz.sub.uni-goettingen.de [PDF] July 1914).
6. ↑ Richard Dedekind: Collected mathematical works . Ed .: Robert Fricke, Emmy Noether, Øystein Ore. tape 3 . Friedr. Vieweg & Sohn, Braunschweig 1932, chap. 62, p. 447-449 ( GDZ - 07/11/1887).
7. ↑ Ernst Zermelo: Investigations on the basics of set theory . I. In: Felix Klein, Walther von Dyck, David Hilbert, Otto Blumenthal (eds.): Math. Ann . tape 65 , no. 2 . B. G. Teubner, 1908, ISSN  0025-5831 , p. 261–281 , doi : 10.1007 / BF01449999 ( gdz.sub.uni-goettingen.de [PDF] July 30, 1907).
8. ↑ Richard Dedekind: What are and what are the numbers? 2nd, unchanged edition. Friedr. Vieweg & Sohn, Braunschweig 1893 ( echo.mpiwg-berlin.mpg.de - first edition: 1888).
9. ↑ Ernst Schröder: About two definitions of finitude and G. Cantor's propositions . In: Imperial Leopoldino-Carolinische Deutsche Akademie der Naturforscher (Ed.): Nova Acta . tape 71 , no. 6 . Johann Ambrosius Barth Verlag, Halle a. P. 1898, p. 303-376 ( biodiversitylibrary.org - February 1896, received May 21, 1896).
10. ↑ Alwin R. Korselt: About a proof of the equivalence theorem . In: Felix Klein, Walther von Dyck, David Hilbert, Otto Blumenthal (eds.): Math. Ann . tape 70 , no. 2 . B. G. Teubner, 1911, ISSN  0025-5831 , p. 294–296 , doi : 10.1007 / BF01461161 ( gdz.sub.uni-goettingen.de [PDF] end of April 1910).
11. ^ Émile Borel: Leçons sur la théorie des fonctions . Gauthier-Villars et fils, Paris 1898, p. 103 ff . ( Text archive - Internet Archive ).
12. ↑ Felix Bernstein: Investigations from set theory . Book printing of the orphanage, Halle a. S. 1901 ( archive.org - Inaugural dissertation with David Hilbert). Felix Bernstein: Investigations from set theory . In: Felix Klein, Walther von Dyck, David Hilbert (eds.): Math. Ann . tape
     61 , no. 1 . B. G. Teubner, 1905, ISSN  0025-5831 , p. 117–155 , doi : 10.1007 / BF01457734 ( gdz.sub.uni-goettingen.de [PDF] unchanged edition except for a few improvements and comments).
13. ↑ The book by Hinkis (2013) examines about 30 pieces of evidence, all before 1973
14. ↑ Felix Hausdorff : Fundamentals of set theory . In: Egbert Brieskorn , Srishti D. Chatterji u. a. (Ed.): Collected works . 1st edition. tape 2 . Springer-Verlag, Berlin / Heidelberg 2002, ISBN 3-540-42224-2 , pp. 587 ( limited preview in Google Book search). Original from 1914
15. ^ Rudolf Lipschitz : Fundamentals of Analysis . In: Fundamentals of Analysis . 1st edition. tape 1 . Max Cohen & Son (Friedrich Cohen) Verlag, Bonn 1877.
16. ↑ Arthur Moritz Schoenflies : The development of the theory of the point manifolds . In: Guido Hauck , August Gutzmer (ed.): Annual report of the German Mathematicians Association . tape 8 , no. 2 . B. G. Teubner, 1900, ISSN  0012-0456 ( DigiZeitschriften ).
17. ↑ Erich Kamke: Set theory (=  Göschen Collection . Volume 999 [a]). 7th edition. Walter de Gruyter & Co., Berlin / New York 1971, ISBN 3-11-003911-7 , § 10, p. 34-36 .
18. ^ Heinz Lüneburg : Combinatorics . In: Elements of mathematics from a higher point of view . 1st edition. tape 6 . Birkhäuser Verlag, Basel u. a. 1971, ISBN 3-7643-0548-7 , pp. 66 .
19. ^ Heinz Lüneburg: Tools and Fundamental Constructions of Combinatorial Mathematics . 1st edition. BI Wissenschaftsverlag, Mannheim u. a. 1989, ISBN 3-411-03194-8 , pp. 349 .