Cauchy criterion

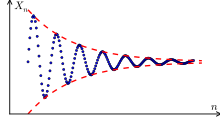
A sequence converges when the distance between the terms of the sequence becomes arbitrarily small in the course of the sequence.

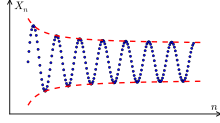
If the distance between the sequence elements does not become arbitrarily small in the course of the sequence, then the sequence diverges.

The (Bolzano) Cauchy criterion (also: principle of convergence, [general] Bolzano-Cauchy criterion or Bolzano-Cauchy convergence criterion ) is a mathematical convergence criterion for sequences and series and of fundamental importance for analysis . It can be used to decide whether a sequence or series of real or complex numbers is convergent or divergent. More generally, the Cauchy criterion can also be applied to sequences of elements of a complete metric space or to series of vectors of a Banach space . It is named after the French mathematician Augustin Louis Cauchy , who published this convergence criterion in his textbook "Cours d'Analyse" in 1821 .

Cauchy criterion for consequences

criteria

A sequence of real or complex numbers converges to a limit value in the real or complex numbers, if there is an index for each , so that the distance between any two sequence members from this index onwards is smaller than . The Cauchy property can be formally described by the fact that ${\displaystyle (a_{n})_{n\in \mathbb {N} }=a_{1},a_{2},\ldots }$ ${\displaystyle \varepsilon >0}$ ${\displaystyle N}$ ${\displaystyle \varepsilon }$

${\displaystyle \forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m,n\geq N\colon \quad \left|a_{m}-a_{n}\right|<\varepsilon }$

applies.

The Cauchy criterion is of fundamental importance for analysis . A sequence of real or complex numbers converges to a limit if and only if it is a Cauchy sequence. This so-called completeness of real or complex numbers is a fundamental property of these number ranges .

The example shows that the Cauchy criterion really depends on the distance between any two sequence members from the index and not just on the distance between successive sequence members. ${\displaystyle a_{n}=\ln(n)}$ ${\displaystyle N}$

example

Let the sequence of real numbers be recursive through ${\displaystyle (a_{n})}$

${\displaystyle a_{n+1}={\tfrac {1}{2}}(1-a_{n}^{2})}$

given, where is. In order to show the convergence of this sequence with the Cauchy criterion, one first calculates ${\displaystyle a_{0}=0}$

${\displaystyle |a_{n+1}-a_{n}|=|{\tfrac {1}{2}}(1-a_{n}^{2})-{\tfrac {1}{2}}(1-a_{n-1}^{2})|={\tfrac {1}{2}}|a_{n}^{2}-a_{n-1}^{2}|={\tfrac {1}{2}}|a_{n}+a_{n-1}|\,|a_{n}-a_{n-1}|\leq {\tfrac {1}{2}}|a_{n}-a_{n-1}|}$,

where the last estimate from the triangle inequality

${\displaystyle |a_{n}+a_{n-1}|\leq |a_{n}|+|a_{n-1}|\leq 1}$

follows, since the individual elements of the sequence are restricted by. If one applies the inequality -mal, one obtains with ${\displaystyle {\tfrac {1}{2}}}$ ${\displaystyle n}$ ${\displaystyle q={\tfrac {1}{2}}}$

${\displaystyle |a_{n+1}-a_{n}|\leq q^{n}|a_{1}-a_{0}|=q^{n+1}}$.

Generally applies to ${\displaystyle m>n}$

${\displaystyle |a_{m}-a_{m-1}|\leq q|a_{m-1}-a_{m-2}|\leq \cdots \leq q^{m-n-1}|a_{n+1}-a_{n}|}$

and through repeated application of the triangle inequality and the geometrical sum formula

${\displaystyle |a_{m}-a_{n}|\leq \sum _{i=0}^{m-n-1}q^{i}|a_{n+1}-a_{n}|\leq {\frac {1-q^{m-n}}{1-q}}q^{n+1}\leq {\frac {1}{1-q}}q^{n+1}=2q^{n+1}=q^{n}<\varepsilon }$

for everyone . The sequence is therefore a Cauchy sequence and therefore convergent. ${\displaystyle n,m>N={\tfrac {\ln \varepsilon }{\ln q}}}$ ${\displaystyle (a_{n})}$

proof

The proof of the Cauchy criterion can be carried out with the Bolzano-Weierstrass theorem as an axiom for the completeness of real or complex numbers. If it is a Cauchy sequence, then one can find an index to such that ${\displaystyle (a_{n})}$ ${\displaystyle \varepsilon =1}$ ${\displaystyle N\in \mathbb {N} }$

${\displaystyle |a_{n}|=|a_{n}-a_{N}+a_{N}|\leq |a_{n}-a_{N}|+|a_{N}|\leq 1+|a_{N}|}$

is for everyone . So the Cauchy episode is over ${\displaystyle n\geq N}$

${\displaystyle \max\{|a_{1}|,|a_{2}|,\ldots ,|a_{N-1}|,1+|a_{N}|\}}$

limited. The Bolzano-Weierstrass theorem now states that the sequence has an accumulation point . Denotes a partial sequence that converges to, results with ${\displaystyle (a_{n})}$ ${\displaystyle a}$ ${\displaystyle (a_{n_{i}})_{i\in \mathbb {N} }}$ ${\displaystyle a}$

${\displaystyle |a_{n}-a|\leq |a_{n}-a_{n_{i}}|+|a_{n_{i}}-a|}$,

that the limit of the entire sequence must be. ${\displaystyle a}$

generalization

More generally, the Cauchy criterion can also be used to study the convergence of sequences of elements of a complete metric space . A sequence of elements converges to a limit value in the set if and only if ${\displaystyle (X,d)}$ ${\displaystyle (x_{i})_{i\in \mathbb {N} }}$ ${\displaystyle x_{i}\in X}$ ${\displaystyle X}$

${\displaystyle \forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m,n\geq N\colon \quad d(x_{m},x_{n})<\varepsilon }$

holds if it is a Cauchy sequence with respect to the metric . In an incomplete metric space, the Cauchy criterion is only a necessary condition for the convergence of a sequence, that is: if a given sequence is not a Cauchy sequence, it diverges. ${\displaystyle d}$

Cauchy criterion for series

criteria

A row

${\displaystyle \sum _{i=1}^{\infty }a_{i}=a_{1}+a_{2}+\ldots }$

with real or complex summands converges to a limit value in the real or complex numbers if and only if ${\displaystyle a_{i}}$

${\displaystyle \forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m>n\geq N\colon \quad |a_{n+1}+a_{n+2}+\ldots +a_{m}|<\varepsilon }$

applies.

Examples

The series converges there ${\displaystyle 1+{\tfrac {1}{4}}+{\tfrac {1}{9}}+{\tfrac {1}{16}}+\ldots }$

${\displaystyle \left|\sum _{i=n+1}^{m}{\frac {1}{i^{2}}}\right|<\left|\sum _{i=n+1}^{m}{\frac {1}{i(i-1)}}\right|=\left|\sum _{i=n+1}^{m}\left({\frac {1}{i-1}}-{\frac {1}{i}}\right)\right|={\frac {1}{n}}-{\frac {1}{m}}<{\frac {1}{n}}\leq {\frac {1}{N}}<\varepsilon }$,

if one chooses what is always possible on the basis of the Archimedean axiom . ${\displaystyle N>{\tfrac {1}{\varepsilon }}}$

On the other hand, the harmonic series diverges , because one chooses , arbitrarily, and , then always applies ${\displaystyle 1+{\tfrac {1}{2}}+{\tfrac {1}{3}}+{\tfrac {1}{4}}+\ldots }$ ${\displaystyle \varepsilon ={\tfrac {1}{2}}}$ ${\displaystyle N}$ ${\displaystyle n\geq N}$ ${\displaystyle m=2n}$

${\displaystyle \left|\sum _{i=n+1}^{m}{\frac {1}{i}}\right|=\left|{\frac {1}{n+1}}+\ldots +{\frac {1}{2n}}\right|\geq n\cdot {\frac {1}{2n}}={\frac {1}{2}}\geq \varepsilon }$.

proof

It has to be shown that the sequence of the partial sums ${\displaystyle (s_{n})}$

${\displaystyle s_{n}=\sum _{i=1}^{n}a_{i}}$

converges. According to the Cauchy criterion for sequences, an index must exist for each such that the inequality applies to indices . Without loss of generality one can assume here . According to the requirement then applies ${\displaystyle \varepsilon >0}$ ${\displaystyle N}$ ${\displaystyle m,n\geq N}$ ${\displaystyle |s_{m}-s_{n}|<\varepsilon }$ ${\displaystyle m>n}$

${\displaystyle |s_{m}-s_{n}|=|(a_{1}+\ldots +a_{m})-(a_{1}+\ldots +a_{n})|=|a_{n+1}+\ldots +a_{m}|<\varepsilon }$

and thus the partial sum sequence converges to a limit value and thus the entire series.

generalization

The Cauchy criterion can also be formulated more generally for series of vectors from a complete normalized space . A set of vectors ${\displaystyle (V,\|\cdot \|)}$ ${\displaystyle v_{i}\in V}$

${\displaystyle \sum _{i=1}^{\infty }v_{i}}$

converges to a limit value in the vector space if and only if ${\displaystyle V}$

${\displaystyle \forall \varepsilon >0\quad \exists N\in \mathbb {N} \quad \forall m>n\geq N\colon \quad \|v_{n+1}+v_{n+2}+\ldots +v_{m}\|<\varepsilon }$

holds, where is the norm of the Banach space . ${\displaystyle \|\cdot \|}$

See also

• Monotony criterion

literature

• Konrad Königsberger : Analysis 1 . Springer-Verlag, Berlin a. a. 2004, ISBN 3-540-41282-4 .
• Otto Forster : Analysis Volume 1: Differential and integral calculus of a variable . 8th edition. Vieweg-Verlag, 2006, ISBN 3-528-67224-2 .

Web links

Wikibooks: Math for Non-Freaks: Cauchy Sequences and the Cauchy Criterion  - Learning and Teaching Materials

Wikibooks: Math for non-freaks: Cauchy criterion for series  - learning and teaching materials

• LD Kudryavtsev: Cauchy criteria . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
• Cauchy Criterion for Convergence . In: PlanetMath . (English)
• Eric W. Weisstein : Cauchy Criterion . In: MathWorld (English).

Individual evidence

1. ↑ See the answer to the question "Origin of Cauchy convergence test" on the Q&A website "History of Science and Mathematics"