Collinearity equation

The collinearity equation is based on the mathematical and geometric principles of collinear mapping . A typical example of a collinear mapping is the central projection . Straight lines are mapped onto straight lines again, division ratios are retained.

Areas of application of the collinearity equation can be found in all areas of optics and optical image recording, especially in optical measurement , photogrammetry and other indirect measurement techniques (e.g. flow velocity of a body of water, flexural strength of materials). Usually, the recorded image points are used to calculate back to the coordinates of the corresponding object points. Image point , projection center and observed object point lie on a straight line .

Derivation of the collinearity equation

Rays of light fall through the hole of a pinhole camera

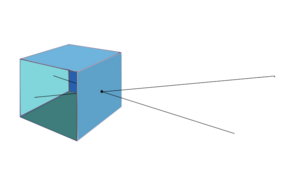
When deriving the collinearity equation, one proceeds in two stages. In stage 1 , one first considers the projection of a 3D object point with respect to the camera coordinate system ( KKS ) in the image plane. The imaging model is the central projection . Then, in stage 2, the transformation from a higher-level national or global world coordinate system ( WCS ) to the KKS is described. Because the position of the camera is only known temporarily and only serves as a measuring instrument. But what you actually need is the relationship between the measured image coordinates and a global 3D coordinate system, in which a 3D model can be calculated at the end that is independent of the camera.

Stage 1 - Central projection as an imaging model of the pinhole camera

In order to mathematically describe the imaging process of a real camera, one first tries to reduce the high complexity of reality in order to obtain a simplified model. As a rule, the pinhole camera model is used for this . The imaging model of the pinhole camera is the central projection . It is a purely geometric model and therefore particularly simple. By means of ray theorems, ratio equations can be set up, one each for the image coordinates and . The collinearity equations are based on this basic idea. ${\displaystyle x}$ ${\displaystyle y}$

Description of the mapping process

Central projection as an idealized imaging model of a camera

To derive this, look at the figure on the left, the cavalier perspective (left). Note that the image plane is in front of the camera (positive position). In contrast to the pinhole camera, where the image plane is behind the projection center (negative position), the resulting image in the positive position is laterally correct and is upright. This simplifies the derivation, the relationships of the central projection remain the same.

A 3D object point is mapped into the image plane via the straight projection beam that goes through the projection center and generates the 2D image point . There is a close relationship between the image coordinate system ( UCS , green axes) located in the image plane and the KKS . The X and Y axes of the KKS are parallel to the corresponding x and y axes of the UCS. The XY plane of the KKS is thus parallel to the image plane. The Z-axis of the KKS is based on the right-hand rule and creates a right-hand system . Therefore the Z-axis depends on the alignment of the axes of the UCS . In this case, the UCS is defined as a standard mathematical coordinate system; i.e., the x-axis points to the right (horizontal) and the y-axis points to the top (vertical). For this reason, the positive Z-axis from the KKS points backwards against the direction of view. ${\displaystyle {\vec {X}}}$ ${\displaystyle O}$ ${\displaystyle {\vec {x}}}$

The extension of the negative Z-axis of the KKS represents the viewing direction of the camera. It penetrates the image plane and creates the main point of the image . The main point is the origin of the image coordinate system ( UCS ). The vertical distance of the projection center from the image plane (line ) is called the camera constant . ${\displaystyle H}$ ${\displaystyle {\overline {OH}}}$ ${\displaystyle c}$

Establishing the equations

If we now look at the side view (on the right in the figure), then, based on the ray laws of the central projection, relationship equations result . The figure shows directly:

${\displaystyle {\frac {y}{-c}}={\frac {Y}{Z}}}$ ${\displaystyle \Leftrightarrow }$ ${\displaystyle y=-c{\frac {Y}{Z}}}$

Because the image plane is along the negative Z-axis, the camera constant must be given a negative sign. And the following applies accordingly: ${\displaystyle c}$ ${\displaystyle x}$

${\displaystyle {\frac {x}{-c}}={\frac {X}{Z}}}$ ${\displaystyle \Leftrightarrow }$ ${\displaystyle x=-c{\frac {X}{Z}}}$

Note: in principle, the axes can also be aligned differently, as in the case of the sensor coordinate system ( SKS , red axes). The origin of the SKS is in the upper left corner of the picture and the x-axis points to the right (horizontal), but the y-axis points downward (vertical). A KKS which is aligned accordingly then has a positive Z-axis that points forward in the direction of view of the camera. This is the common practice in computer vision . In photogrammetry , however, a different alignment of the axes has been established for historical reasons.

Stage 2 - Transformation from WCS to KKS

Next, the relationship between the global world coordinate system and the local camera coordinate system will be described. With such a coordinate transformation , one considers a point with respect to two different reference systems which can be shifted from one another and rotated as required. So you need a translation (displacement) and a rotation (rotation) to formulate the mathematical relationship. It is easiest to first carry out the translation, so that the reference systems share a common origin, that is, they are more or less on top of each other. The rotation is then carried out. ${\displaystyle P}$

Coordinate transformation from WCS to KKS with a focus on translation.

To do this, we consider the figure on the right. Two reference systems are shown here: the WCS (red axes) and the KKS (blue axes). A point has in relation to the WCS the coordinates (red) and with respect to the PPS the coordinates (blue). The rules of vector arithmetic must be observed here. This means that you can only combine vectors with respect to one and the same reference system. This poses a problem for us because the vector (blue) is defined with respect to the KKS . However, we need it with regard to the WCS . ${\displaystyle P}$ ${\displaystyle {\vec {X}}_{a}}$ ${\displaystyle {\vec {X}}_{b}}$ ${\displaystyle {\vec {X}}_{b}}$

There is a trick here: by subtracting the translation vector (red) from , the vector results again in the parallelogram as a difference vector (red). The vector searched for is parallel to the difference vector and thus maintains its direction with respect to the KKS . So you don't move the coordinate system, but the point and stay in the same reference system. ${\displaystyle {\vec {X}}_{0}}$ ${\displaystyle {\vec {X}}_{a}}$ ${\displaystyle {\vec {X}}_{b}}$ ${\displaystyle {\vec {X}}_{diff}}$ ${\displaystyle {\vec {X}}_{b}}$ ${\displaystyle {\vec {X}}_{diff}}$

Then you can transfer the coordinates of the difference vector to the target system by multiplication with a general rotation matrix . The entire coordinate transformation can be formulated as follows in vector-matrix notation. ${\displaystyle R}$

${\displaystyle {\vec {X}}_{b}=R\cdot {\vec {X}}_{diff}}$ , With ${\displaystyle {\vec {X}}_{diff}={\vec {X}}_{a}-{\vec {X}}_{0}}$

And the components are written in detail:

${\displaystyle {\begin{bmatrix}X_{b}\\Y_{b}\\Z_{b}\end{bmatrix}}_{KKS}={\begin{bmatrix}r_{1,1}&r_{1,2}&r_{1,3}\\r_{2,1}&r_{2,2}&r_{2,3}\\r_{3,1}&r_{3,2}&r_{3,3}\end{bmatrix}}_{WKS\rightarrow KKS}\cdot {\begin{bmatrix}X_{diff}\\Y_{diff}\\Z_{diff}\end{bmatrix}}_{WKS}}$ , With ${\displaystyle {\begin{bmatrix}X_{diff}\\Y_{diff}\\Z_{diff}\end{bmatrix}}_{WKS}={\begin{bmatrix}X_{a}\\Y_{a}\\Z_{a}\end{bmatrix}}_{WKS}-{\begin{bmatrix}X_{0}\\Y_{0}\\Z_{0}\end{bmatrix}}_{WKS}}$

The indicators KKS and WKS should each show the assignment of the coordinates to a reference system.

For the next step it is useful to represent each row of the rotation matrix as a vector (with row index ). Note that by default a vector is defined as a column vector, which is why it is transposed to get a row vector. ${\displaystyle R}$ ${\displaystyle {\vec {r}}_{i}^{T}}$ ${\displaystyle i}$

${\displaystyle R_{WKS\rightarrow KKS}={\begin{bmatrix}r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{bmatrix}}={\begin{bmatrix}{\vec {r}}_{1}^{T}\\{\vec {r}}_{2}^{T}\\{\vec {r}}_{3}^{T}\end{bmatrix}}}$

Stage 3 - Summary of Transformation

If you now insert the equations for coordinate transformation from WCS to KKS into the above relationship equations, you get the collinearity equations . First in compact form:

${\displaystyle x=-c{\frac {{\vec {r}}_{1}^{T}\cdot {\vec {X}}_{diff}}{{\vec {r}}_{3}^{T}\cdot {\vec {X}}_{diff}}}}$

${\displaystyle y=-c{\frac {{\vec {r}}_{2}^{T}\cdot {\vec {X}}_{diff}}{{\vec {r}}_{3}^{T}\cdot {\vec {X}}_{diff}}}}$

and multiplied again:

${\displaystyle x=-c{\frac {r_{11}\cdot (X-X_{0})+r_{12}\cdot (Y-Y_{0})+r_{13}\cdot (Z-Z_{0})}{r_{31}\cdot (X-X_{0})+r_{32}\cdot (Y-Y_{0})+r_{33}\cdot (Z-Z_{0})}}}$

${\displaystyle y=-c{\frac {r_{21}\cdot (X-X_{0})+r_{22}\cdot (Y-Y_{0})+r_{23}\cdot (Z-Z_{0})}{r_{31}\cdot (X-X_{0})+r_{32}\cdot (Y-Y_{0})+r_{33}\cdot (Z-Z_{0})}}}$

Note: The indicators ( WKS , KKS and BKS ) were deliberately left out here in order to simplify the formula.

These collinearity equations represent the mapping process between the coordinates of a 3D point (in the world coordinate system) and its 2D point (in the image coordinate system) in a compact form. Because of the fraction, it is a non-linear relationship. However, using homogeneous coordinates, it is possible to formulate the relationship between the central projection in a linear manner (see projection matrix (computer vision) ).

Note: In the literature, the rotation matrix as described above is often not used. Instead, the matrix of the reverse rotation from the local to the global system ( KKS to WKS ) is used. This corresponds to the transposed matrix , which turns the row vectors of the matrix into column vectors. If you put this transposed matrix in the collinearity equations, then there are other indices of the rotation parameters , where the row index and the column index are interchanged, i.e. H. . ${\displaystyle R^{T}}$ ${\displaystyle R}$ ${\displaystyle r_{ij}}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle r_{ji}}$

Variant 2 ( ) ${\displaystyle R^{T}}$ :

${\displaystyle x=-c{\frac {r_{11}\cdot (X-X_{0})+r_{21}\cdot (Y-Y_{0})+r_{31}\cdot (Z-Z_{0})}{r_{13}\cdot (X-X_{0})+r_{23}\cdot (Y-Y_{0})+r_{33}\cdot (Z-Z_{0})}}}$

${\displaystyle y=-c{\frac {r_{12}\cdot (X-X_{0})+r_{22}\cdot (Y-Y_{0})+r_{32}\cdot (Z-Z_{0})}{r_{13}\cdot (X-X_{0})+r_{23}\cdot (Y-Y_{0})+r_{33}\cdot (Z-Z_{0})}}}$

In addition, the collinearity equation is usually extended to the effect that a reference is made to a sensor coordinate system lying in the image plane (or to the fiducial mark system in the case of analog images). Ie, you add the coordinates of the main point. It should be noted, however, that the alignment of the axes between the sensor system and the image coordinate system change. In particular, the y-axis of the SKS is directed in the opposite direction to the BKS . In addition, the translation vector (coordinates of the main point) from the UCS to the SKS is replaced by the vector directed in the opposite direction, whereby (minus times minus results in plus) the coordinates of the main point are added.

Variant 3 (regarding SKS, ) ${\displaystyle R}$ :

${\displaystyle x_{SKS}=x_{H,SKS}-c{\frac {r_{11}\cdot (X-X_{0})+r_{12}\cdot (Y-Y_{0})+r_{13}\cdot (Z-Z_{0})}{r_{31}\cdot (X-X_{0})+r_{32}\cdot (Y-Y_{0})+r_{33}\cdot (Z-Z_{0})}}}$

${\displaystyle y_{SKS}=y_{H,SKS}+c{\frac {r_{21}\cdot (X-X_{0})+r_{22}\cdot (Y-Y_{0})+r_{23}\cdot (Z-Z_{0})}{r_{31}\cdot (X-X_{0})+r_{32}\cdot (Y-Y_{0})+r_{33}\cdot (Z-Z_{0})}}}$

Using the collinearity equation

This equation is used in many ways, especially in photogrammetry. It is used for camera calibration, the determination of the external orientation ( georeferencing ) and for the calculation of 3D models. The collinearity equation serves as the basic equation for a least squares adjustment . In principle, any number of correction terms can be added to this form of adjustment calculation, e.g. B. for the determination of distortion parameters during camera calibration. Because of this flexibility, the collinearity equation has a special meaning.

See also

• collinear
• Inner and outer orientation
• Relative and absolute orientation
• Photogrammetry

literature

• Karl Kraus : Photogrammetry, Volume 1 - Fundamentals and Standard Methods, Ferd. Dümmlers Verlag, Bonn 1997 (6th edition), ISBN 3-427-78646-3 .
• Thomas Luhmann: Close-range photogrammetry - basics, methods and applications , Wichmann, Berlin and Offenbach 2010 (3rd edition), ISBN 978-3-87907-479-2