Phyllotaxis

The leaves of the sunflower are arranged alternately in a spiral

Spiral, spiral, alternate-spiral

Phyllotaxis ( ancient Greek φύλλον phyllon , German 'leaf' , ταξις taxis 'arrangement') is a name for the regular arrangement of the leaves of plants . Leaf position and leaf stand are synonymous terms.

history

The columnar permanent (cauline) sheets are not randomly arranged. Leonardo da Vinci already pointed out the regular arrangement of the sheets in his diaries .

A Swiss naturalist named Charles Bonnet founded the modern phyllotaxis idea . In 1754 he was the first to discover the following arrangement in the screwy phyllotaxis: One leaf per node, which corresponds to the area of ​​the stem axis where one or more leaves attach. The successive sheets are each shifted to one another by a certain angle. He found that the leaves are arranged in a spiral around a branch. Bonnet called this spiral the genetic spiral .

The botanist Karl Friedrich Schimper is considered to be the one who mathematically developed the underlying principles. The doctrine of the leaf position was established through his work around 1830. Several technical terms still used today were coined by Schimper - such as divergence , cycle , orthostiches and parastiches .

Alexander Braun was encouraged to do further research by Schimper. Because of his contributions, one also speaks of the Schimper-Braun leaf position theory - Schimper-Braun main series.

Alternate, alternate-distichous		Opposite, opposite-distichous

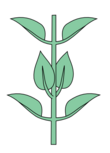
Cross-opposite, opposite-decussate		The swallow-root gentian with cross-opposed leaves

Whorled, whorled		The fir frond with whorled leaves

Basic types of leaf position

Change-over

Here the leaves are individually alternating along the stem axis , i. i.e., none is on the same level as another (alternate).
Mostly alternate leaves are:

• spiral, spiral (dispersed) (dispersed, spiral): The leaves are neither at ≈90 ° nor at ≈180 °, but at a different, but always fixed, angle to each other. The single-sheet Nodi form a helical line (helix). Different arrangements are possible, see under structure.
• two-rowed (distichous, two-ranked 1/2; ≈180 °): The leaves are on the opposite side of the stem, so that two alternating rows of leaves are formed. There is one leaf per nodus, two vertical lines (orthostiches) with leaf organs are created.

Spirodistichie is the name for the two-line or distich leaf position, in which the two straight lines gradually rotate around the axis.

Opposite

The leaves are opposite each other along the stem axis (opposite-superposed; -distichous, two-lined). Sometimes the leaves are only a little apart, then they are almost opposite (subopposite).

Most of the time, the pairs of leaves (dimeric, two-part whorl) are themselves cross- opposite (opposite-decussate, dekussiert ): Every two pairs of leaves that follow one another on the stem are approximately at right angles to each other, alternating. Often in the labiate family . There are four lines (orthostitching) with leaf organs.

This type of leaf position, in which the leaves are arranged at a certain so-called "equidistance angle" (angular distance between the leaves), is very common. The arrangement follows two rules, on the one hand the equidistance rule (the angular distance between all leaves is the same) and on the other hand the alternation rule (leaves of two consecutive (leaf) rows are offset from one another). This is how longitudinal rows (ortho stitches) are formed.

Whorl or whorled

In the whorled or whorled (organ circle ) basic type, at least two leaves always arise on the shoot (in the most common case two or three: di-, tri, -... polymeric whorls) at the same height at the same node.

Rosette

Due to the reduced growth in length of the stem, it can happen that many leaves sit at approximately the same height. In this case one speaks of a leaf rosette . Often there is a leaf rosette at the end of the stem. If the rosette is basic one speaks of a basic rosette .

Basic

The leaves are located just above or directly on the surface of the soil (radical, basal, subbasal), so that all leaves appear to arise from the soil. In many plants, these so-called basal leaves have a different shape than the stem leaves . see rosette plant

• 

  The mean plantain has only basal leaves

• 

  Leaves riding (equitant), scaly leaf (imbricate), parted, tufted (fascicled)

• 

  Cheilocostus speciosus leaves arranged in a spiral on one side

Further arrangements

• Riding (equitant): The leaves are sessile, with, towards the stem axis, a channel-shaped, tubular base. The first leaf includes the stem axis and the subsequent leaves then each include the previous one at the edges.
• Pseudo whorl, pseudo whorl, sham whorl (pseudowhorled): The three or more leaves are spiral, screw-like, with a flat pitch, arranged in knots close to one another, so that it looks like a whorl.
• Roof tiles, scaly (imbricate, scale leaf): leaves arranged alternately, overlap (stem axis no longer visible).
• Parted, in clusters (fascicled): leaves arise on all sides on horizontal rungs, curved in two rows in the horizontal plane ( fir , yew )
• Single row, one-sided (spiro) (monistichous, secund, one-sided): The leaves are only arranged on one side, as in Cheilocostus speciosus .
• Arranged at the tip of the stem, like a tuft (acrocaulis).

construction

Basic spiral, divergence and cycle

If one such proceeds at a stem with alternate leaves from the bottom upwards, that it touches all the sheets as they follow each other up, so to describe a the stem umwindende spiral line , the so-called genetic or basic spiral (spiral, unijugate).

This results in the peculiarity that the piece of the stem periphery , which one has to go around with the spiral to get from one leaf to the next, is the same size for all leaves of the stem. This part of the arc is called divergence (of the leaves ); it can be expressed in fractions of the number of axis revolutions in the cycle and the number of leaves in a cycle, i.e. a number between 0 and 1/2.

The part of the basic spiral that one has to cover in order to get from one initial leaf to the next vertically above leaf is called the cycle (outdated: cycle ).

The leaf arrangement can then be related to the Fibonacci numbers , which are related to the golden ratio . See Fibonacci sequences in nature . But there are also other divergence fractions that do not fit in this series. These other divergence angles correspond to e.g. B. the consequences of Lucas .

But there can be more than one basic spiral, these systems are called bi-, tri- or multijugate.

The multijugate patterns are often similar to the spiral patterns, the only way to recognize them is to count the number of spirals visible in the pattern (called parastiches). If the number of parastiches don't have a common divisor other than 1, the pattern is a spiral phyllotaxis. If the number of parastiches have a common divisor k, then the pattern is multijugate (more precisely k-jugate) and there are k elements at each node.

There are also other systems that have a certain pattern that does not match any of the named (spiral, distichous, multijugal, whorled). There are also irregular systems.

Leaf lines (orthostitching)

With some plants these breaks are rational (broken) parts of the periphery, from which it follows that every time after a certain number of leaves a leaf is exactly above the original leaf. If you have a leaf position with a divergence of 2/5 (2 circles / 5 orthostitches); five-line (pentastichous, five ranked; 144 °), in which the spiral rises from leaf 1, then leaf 6 is the first that is again vertically above the original leaf. Likewise, sheet 7 stands above sheet 2, sheet 8 above sheet 3, etc. The position of the leaves can also be two-line, three-line (tristichous, tree ranked 1/3; 120 °) or eight-line (octastichous or eigth ranked 3/8; 135 °), ( 5/13; 138 ° 27 ') etc.

The divergence angle in this series tends to the so-called limit divergence angle of 137 ° 30 '28 "(137.5078 °) ( golden angle ). With this blade position, theoretically no leaf is directly over another, which would mean ideal use of solar radiation.

With these leaf positions, the leaves are on the axis in so-called ortho stitches (straight lines), the number of which corresponds to the denominator in the leaf position fraction. In these cases, the leaves that sit on the side of a stem can be connected by a number of straight lines , which are called leaf lines ( orthostiches ).

In phylogenesis, angular displacements (screwing) resulted in new leaf positions in many plant species, in which the leaves are no longer on straight lines (ortho stitches), but on lines wound in the same direction, so-called spiro stitches (screw lines) ( ortho stitches that are slightly twisted) on the basic spiral are located.

In the case of branched stems, the basic spiral of the main axis and the branches are the same or different:

• Homodromy, homodrome, equivalency ; Designation of the case where the direction of the leaf spiral is the same on two equivalent rungs.
• Antidromia, (amidromia), antidrom, inequality ; Term for the direction of rotation of the leaf spiral of a side branch when it is opposite to the direction of rotation of the main axis.

Parastitches

Parastitches (diagonal lines, secondary spirals) are the inclined helical lines perpendicular to the basic spiral, alternating right and left. In a spiral lattice, the eye tends to connect the nearest points in spirals. They are therefore easily recognizable by the compressed shoot axes, through the contact between the younger leaves and the neighboring leaves of the older revolutions of the basic spiral. The difference in the sheet numbers of the consecutive sheets that lie on the parastitch is equal to the number of rectified rows. In this way the sheet numbers of all sheets can be determined. The basic spiral and the divergence can then be recognized.

If the leaves are arranged in very narrow, flat spirals and it is not possible to count the spiro stitches (ortho stitches), this type is called parastichous.

Golden cut

Golden ratio in the leaf stand

In plants it has been found that primitive species have a divergence (angle between three consecutive leaves of the basic spiral, see adjacent figure) that corresponds to the golden ratio .

There are essentially two theories as to why this is the case with plants:

• The leaves take up a lot of space and displace other species.
• The sugar solution, which is produced by photosynthesis, is evenly distributed to almost all the vascular bundles of the phloem , as the leaves flow into the branch exactly above another.

Control via hormones

The primary growth of the plant takes place in the apical meristem (so-called apex , also bud ). The apex rotates on its own axis as it grows; leaf primordia are always formed, d. H. Leaf systems, where the leaves later form.

The hormone auxin is transported from the apex to the leaf system. The auxin absorption by the already existing primordium directs the position of the new primordium. Auxin is absorbed by the already existing primordia and thus removed from the immediate vicinity (lateral reduction). The new primordium cannot arise directly next to the old leaf system, since an accumulation of auxin can only begin at a certain minimal distance. Because the youngest leaf primordium absorbs the auxin more strongly than the second youngest, the new primordium arises closer to the second youngest than to the youngest primordium. This is the reason why the angle of divergence between two successively formed primordia corresponds to a typical angle of 137.5 ° (“golden ratio”).

Petals

Since petals are special formations of normal leaves, the basic arrangements of the phyllotaxis are found, sometimes with adhesions of the individual leaves, also in the flowers themselves and in the inflorescences .

literature

• Didier Reinhard u. a .: Regulation of phyllotaxis by polar auxin transport. In: Nature . 426, 2003, pp. 255-260, doi: 10.1038 / nature02081 .
• Roger V. Jean: Phyllotaxis: A Systemic Study in Plant Morphogenesis. Cambridge Univ. Press, 1994, 1995, 2009, ISBN 978-0-521-40482-2 .
• Christel Kasselmann : aquarium plants. Ulmer Verlag, Stuttgart 1995; 2nd, revised and expanded edition 1999, ISBN 3-8001-7454-5 , p. 481 f. and 485 ( leaf position ).

Web links

Commons : Phyllotaxis  - collection of images, videos and audio files

• Phyllotaxy (Arrangement of Leaves) on biologydiscussion.com, accessed December 8, 2017.
• Phenomenology of leaf position (phyllotaxis). University of Koblenz.
• Phyllotaxis website of the mathematician Michael Becker.
• Alfred Höhn: Fibonacci and Lucas sequences in the phyllotaxis. (PDF; 1.85 MB).
• Are plants aesthetes or mathematicians? science-texts.de.

Individual evidence

1. ↑ Phyllotaxis and leaf position . Duden online
2. ↑ I. Adler, D. Barabe and RV Jean: A History of the Study of Phyllotaxis. In: Annals of Botany. 80 (3), 1997, 231-244, doi: 10.1006 / anbo.1997.0422 , online (PDF; 215 kB), on nicorg.pbworks.com.
3. ↑ PhiTaxis: Fibonacci digital simulation of spiral Phyllotaxis on sciteneg.com, accessed June 19, 2017.
4. ↑ Phyllotaxis Classification ( Memento March 9, 2017 in the Internet Archive ) math.smith.edu, accessed June 19, 2017.
5. ^ Claus Peter Ortlieb , Caroline von Dresky, Ingenuin Gasser, Silke Günzel: Mathematical modeling. 2nd edition, Springer, 2013, ISBN 978-3-658-00534-4 , pp. 31-46.
6. ↑ Jonathan Swinton, Erinma Ochu, The MSI Turing's Sunflower Consortium: Novel Fibonacci and non-Fibonacci structure in the sunflower: results of a citizen science experiment. In: Royal Society Open Science. 5, 2016, doi: 10.1098 / rsos.160091 .
7. ^ Meyer's Large Conversational Lexicon. Volume 3, Leipzig 1905, p. 34 .: Leaf position at Zeno.org .
8. ^ Joachim W. Kadereit, Christian Körner, Benedikt Kost, Uwe Sonnewald: Strasburger - Textbook of Plant Sciences. 37th edition, Springer, 2014, ISBN 978-3-642-54434-7 , pp. 106 ff.
9. ^ K. Giesenhagen: Giesenhagen textbook of botany. 9th edition, Springer, 1924, ISBN 978-3-663-15325-2 , p. 12.