Lagrange resolvent

In the theory of algebraic equations, the Lagrange resolvent is an auxiliary quantity formed from the zeros ( roots ) of a polynomial and the primitive roots of unit , which satisfies another polynomial equation, the resolvent equation. In addition to the Lagrange resolvent, there are also other resolvents.

Bulk

It was introduced by Joseph-Louis Lagrange around 1770 to investigate the solvability of algebraic equations of a higher degree by radicals , that is, by closed expressions from the coefficients of the equation that only use the basic arithmetic operations and the extraction of roots .

Corresponding formulas for third and fourth degree polynomials had been known since Nicolo Tartaglia and others, and the extension to higher degree polynomials was one of the main goals of algebraic research until the early 19th century, when the work of Evariste Galois and Niels Henrik Abel made it clear that this is generally not possible for equations of the fifth degree and higher. In analyzing the problem, Lagrange recognized that the investigations of quantities that remain invariant in the permutation of the roots are important in this context, which ultimately led to the solution of the problem about the structure of the permutation groups involved by Galois in the 1830s ( According to Galois, a polynomial equation can be solved by radicals if and only if the Galois group of the polynomial is a solvable group ).

One considers the polynomial -th degree ${\displaystyle n}$

${\displaystyle f(x)=x^{n}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+a_{n-3}x^{n-3}+\dotsb +a_{1}x+a_{0}=\prod _{i=1}^{n}(x-x_{i})}$

with the roots and known coefficients that are elementary symmetric polynomials of the roots. ${\displaystyle x_{i}}$ ${\displaystyle a_{i}}$

The Lagrange resolvent is the expression

${\displaystyle t=x_{1}+\beta x_{2}+\beta ^{2}x_{3}+\beta ^{3}x_{4}+\dotsb +\beta ^{n-1}x_{n}}$

with a primitive -th root of unity (it fulfills ). It is assumed that there are no multiple roots (the roots are different in pairs). ${\displaystyle n}$ ${\displaystyle \beta \neq 1}$ ${\displaystyle {\beta }^{n}=1}$ ${\displaystyle x_{i}}$

The total sizes are obtained by permutating the . The roots of the output equation should be expressed by the and the coefficients . ${\displaystyle x_{i}}$ ${\displaystyle k=n!}$ ${\displaystyle t_{i}}$ ${\displaystyle x_{i}}$ ${\displaystyle t_{i}}$ ${\displaystyle a_{i}}$

The Lagrange resolvents themselves are the roots of the resolvent equation : ${\displaystyle g}$

${\displaystyle g(x)=\prod _{i=1}^{k}(x-t_{i})=0}$

The resolvent equation, like the output equation, is invariant by interchanging the roots of . The coefficients of the resolvent equation are as elementary symmetric functions in the symmetric functions in the roots of and according to the main theorem for elementary symmetric functions polynomials in the (the elementary symmetric functions of the roots of ). ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle t_{i}}$ ${\displaystyle f}$ ${\displaystyle a_{i}}$ ${\displaystyle f}$

Lagrange (and independently Vandermonde ) showed that the well-known solution formulas of the third and fourth degree equations (in the case of the cubic equation, the Cardano formula ) can be uniformly explained by considering the resolvent equation . In the case of the cubic equation, it is sixth degree, but it can be reduced to a quadratic equation. The equation of the fourth degree leads to a resolvent equation of the 24th degree, which can be reduced to a cubic equation. With the fifth degree equation , Lagrange encountered the limitations of his method, which in this case did not simplify the problem. Abel later showed that it is not generally solvable by radicals.

In general, resolvents are understood to mean polynomials or, more generally, rational functions in the roots of the initial equation (formed with other known quantities such as the coefficients of ), from which the roots of can be clearly obtained, and the resolvent equation is an auxiliary equation for determining the resolvent. According to Lagrange, the resolvents should occupy as few values ​​as possible with permutation of the roots of . According to the construction, the resolvent equation is invariant like the initial equation with interchanging the roots of . ${\displaystyle f(x)=0}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle f}$

With these more general resolvents the Galois group of the equation and its subgroups can be examined (with associated resolvents) and they were an integral part of the treatment of Galois theory in textbooks in the 19th century (in this context one speaks of Galois resolvents). The term resolvent originally comes from Leonhard Euler (1738) in connection with the equation of the fourth degree and the name comes from the Latin ( resolvere for to resolve). With these classical methods of solving the equation of the fourth degree , one is led to an auxiliary equation of the third degree, which is called the cubic resolvent of the quartic.

Example quadratic equation

The case is presented here to show the principle, although there is no simplification by the resolvent method.

${\displaystyle f(x)=x^{2}+Ax+B=(x-x_{1})(x-x_{2})=0}$

With and . ${\displaystyle A=-x_{1}-x_{2}}$ ${\displaystyle B=x_{1}x_{2}}$

The Lagrange resolvents are (with the square roots of unity used here: +1, −1):

${\displaystyle t_{1}=x_{1}-x_{2}}$ and ${\displaystyle t_{2}=x_{2}-x_{1}=-t_{1}}$

The resolvent equation is also quadratic:

${\displaystyle g(x)=(x-t_{1})(x-t_{2})=(x-t_{1})(x+t_{1})=x^{2}-t_{1}^{2}=0}$

The solution is also called the discriminant of the quadratic equation . ${\displaystyle t_{1}^{2}}$ ${\displaystyle f}$

The roots of the initial equation are given by the resolvents and coefficients over: ${\displaystyle f}$ ${\displaystyle A,B}$

${\displaystyle x_{1}={\frac {t_{1}-A}{2}}}$ and ${\displaystyle x_{2}={\frac {-t_{1}-A}{2}}}$

With results and this inserted results in the usual solution formulas of the quadratic equation. ${\displaystyle B=x_{1}x_{2}}$ ${\displaystyle t_{1}=\pm {\sqrt {(A^{2}-4B)}}}$

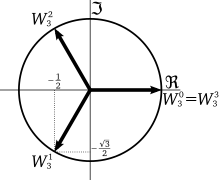
Example cubic equation

Consider the standardized cubic equation with leading coefficient 1 and the roots : ${\displaystyle (x,y,z)}$

${\displaystyle f(S)=(S-x)(S-y)(S-z)=S^{3}+AS^{2}+BS+C}$

The coefficients are the elementary symmetric functions in the roots : ${\displaystyle A,B,C}$ ${\displaystyle x,y,z}$

${\displaystyle A=-x-y-z}$, , ${\displaystyle B=xy+yz+xz}$ ${\displaystyle C=-xyz}$

After the resolvent construction, an auxiliary equation is sought from which the roots can be determined. ${\displaystyle x,y,z}$

The Lagrange resolvent is:

${\displaystyle t=x+ay+a^{2}z}$,

wherein a third primitive root of unity, therefore a solution of , that is to say one of the two values or . By swapping the roots you get six different ones ${\displaystyle a}$ ${\displaystyle a^{3}=1}$ ${\displaystyle a\neq 1}$ ${\displaystyle a_{1}=-1/2+i{\sqrt {3}}/2}$ ${\displaystyle a_{2}=-1/2-i{\sqrt {3}}/2}$ ${\displaystyle x,y,z}$ ${\displaystyle t_{i}}$

The third roots of unity

${\displaystyle t_{1}=x+ay+a^{2}z}$

${\displaystyle t_{2}=z+ax+a^{2}y=at_{1}}$

${\displaystyle t_{3}=az+a^{2}x+y=a^{2}t_{1}}$

${\displaystyle t_{4}=x+az+a^{2}y}$

${\displaystyle t_{5}=ax+a^{2}z+y=at_{4}}$

${\displaystyle t_{6}=a^{2}x+z+ay=a^{2}t_{4}}$

The equation for , and can be determined if the resolvents are known. ${\displaystyle t_{1}}$ ${\displaystyle t_{4}}$ ${\displaystyle A=-x-y-z}$ ${\displaystyle x,y,z}$

The six values ​​for can now be understood as the solution of another equation of the 6th degree, the resolvent equation: ${\displaystyle t}$

${\displaystyle g(X)=(X-t_{1})(X-t_{2})(X-t_{3})(X-t_{4})(X-t_{5})(X-t_{6})=0}$

The following arithmetic process shows that there is a quadratic equation. ${\displaystyle g}$

Because and is ${\displaystyle a^{2}+a+1=0}$ ${\displaystyle a^{3}=1}$

${\displaystyle (X-t_{1})(X-t_{2})(X-t_{3})=(X-t_{1})(X-at_{1})(X-a^{2}t_{1})=X^{3}-t_{1}^{3}}$

${\displaystyle (X-t_{4})(X-t_{5})(X-t_{6})=(X-t_{4})(X-at_{4})(X-a^{2}t_{4})=X^{3}-t_{4}^{3}}$

Inserted results in:

${\displaystyle g(X)=(X^{3}-t_{1}^{3})(X^{3}-t_{4}^{3})=X^{6}-(t_{1}^{3}+t_{4}^{3})X^{3}+t_{1}^{3}t_{4}^{3}}$

If you set

${\displaystyle u=t_{1}^{3}}$

${\displaystyle v=t_{4}^{3}}$,

writes the equation

${\displaystyle g(X)=X^{6}-(u+v)X^{3}+uv}$.

After substitution

${\displaystyle Z=X^{3}}$

one obtains the quadratic equation . ${\displaystyle g(Z)=Z^{2}-(u+v)Z+uv}$

This can also view so that under permutation of the roots while six pictures have ( , , , , , ), but (because only two ), yourself and why you can take as a resolvent. ${\displaystyle t_{1}}$ ${\displaystyle x,y,z}$ ${\displaystyle t_{i}}$ ${\displaystyle t_{1}}$ ${\displaystyle at_{1}}$ ${\displaystyle a^{2}t_{1}}$ ${\displaystyle t_{4}}$ ${\displaystyle at_{4}}$ ${\displaystyle a^{2}t_{4}}$ ${\displaystyle u={t_{1}}^{3}}$ ${\displaystyle a^{3}=1}$ ${\displaystyle v={t_{4}}^{3}}$ ${\displaystyle g(Z)=(Z-u)(Z-v)}$

Certainly you can and only by the roots of the original equation to express. This can be shown by direct calculation or with the following argumentation: ${\displaystyle u+v}$ ${\displaystyle uv}$ ${\displaystyle x,y,z}$

The elementary symmetric functions of (i.e. and ) are invariant when interchanged and can thus be expressed by their elementary symmetric functions, i.e. by . ${\displaystyle u,v}$ ${\displaystyle u+v}$ ${\displaystyle uv}$ ${\displaystyle x,y,z}$ ${\displaystyle A,B,C}$

Explicitly results in and . ${\displaystyle u+v=-2A^{3}+9AB-27C}$ ${\displaystyle uv={(A^{2}-3B)}^{3}}$

In Galois theory, the solvability by radicals is shown by the fact that the symmetry group of the three roots is solvable, because there is the chain (the alternating group of even permutations), 1 (identity), where (order 3) is cyclic and also the quotient group (Order 2). swapped separately and with each other. The primitive root is the generator of the cyclic group . ${\displaystyle S_{3}}$ ${\displaystyle S_{3},A_{3}}$ ${\displaystyle A_{3}}$ ${\displaystyle S_{3}/A_{3}}$ ${\displaystyle A_{3}}$ ${\displaystyle (t_{1},t_{2},t_{3})}$ ${\displaystyle (t_{4},t_{5},t_{6})}$ ${\displaystyle a}$ ${\displaystyle A_{3}}$

4th degree equations

The discussion can be carried out analogously to the cubic equation with Lagrange resolvents, but also with other resolvents. In the following, resolvents are used that are no longer linear in the roots of the initial equation , but are the invariants of subsets of the full symmetry group of the roots in the equation of the fourth degree. ${\displaystyle x_{i}}$ ${\displaystyle S_{4}}$

Let the reduced quartic equation (the third degree term was removed with a Tschirnhaus transformation ) ${\displaystyle f}$

${\displaystyle h(x)=X^{4}+aX^{2}+bX+c}$.

Form the resolvents

${\displaystyle t_{1}=x_{1}x_{2}+x_{3}x_{4}}$

${\displaystyle t_{2}=x_{1}x_{3}+x_{2}x_{4}}$

${\displaystyle t_{3}=x_{1}x_{4}+x_{2}x_{3}}$.

Then these satisfied the resolvent equation (cubic resolvent):

${\displaystyle g(t)=(t-t_{1})(t-t_{2})(t-t_{3})=t^{3}+vt^{2}+wt+z}$

With

${\displaystyle v=-a}$, , . ${\displaystyle w=-4c}$ ${\displaystyle z=4ac-b^{2}}$

In addition, the resolvents are converted into themselves by the permutations of Klein's group of four . This is part of the normal divider chain , , , , identity to the resolution of the symmetric group (with the cyclic group of order 2 and the Alternating group of order 4). The factor groups are each cyclical group. This chain explains the solvability of the fourth degree equation by radicals in Galois theory. ${\displaystyle V}$ ${\displaystyle S_{4}}$ ${\displaystyle A_{4}}$ ${\displaystyle V}$ ${\displaystyle C_{2}}$ ${\displaystyle S_{4}}$ ${\displaystyle C_{2}}$ ${\displaystyle A_{4}}$

This is an example of resolvents who are no longer invariant under the full symmetry group of the permutation of the roots, but only under a subgroup. ${\displaystyle S_{4}}$

5th degree equations

Lagrange was only able to reduce the problem to one resolvent, which assumed 24 different values ​​with permutation of the roots

${\displaystyle t={(x_{1}+ax_{2}+a^{2}x_{3}+a^{3}x_{4}+a^{4}x_{5})}^{5}}$

with the roots of the quintic and the primitive fifth root of unity . The resolvent equation was thus of degree 24. ${\displaystyle x_{i}}$ ${\displaystyle a}$

In 1861 Arthur Cayley found a resolvent that was transformed into only six different values ​​with permutation of all roots:

${\displaystyle t={(x_{1}x_{2}+x_{2}x_{3}+x_{3}x_{4}+x_{4}x_{5}+x_{5}x_{1}-x_{1}x_{3}-x_{2}x_{4}-x_{3}x_{5}-x_{4}x_{1}-x_{5}x_{2})}^{2}}$

This resolvent is also known as the Malfatti resolvent (after Gianfrancesco Malfatti , who introduced it as early as 1771).

It takes on six values ​​with permutation of the roots, so it satisfies a resolvent equation of the sixth degree. A quintic with rational coefficients is solvable by radicals if and only if one of the solutions is rational. ${\displaystyle t}$

In general, as shown in Galois theory, it is no longer solvable by radicals, which also applies to all equations of a higher degree . ${\displaystyle n>5}$

Galois Resolvents

For a given algebraic equation of degree, Galois considered the symmetries that exist in relation to the roots. Can be formally these symmetries, if the roots are different, by means of the entirety of the polynomials characterize that upon insertion of the roots of the equation vanish identically: . The group of permutations of the which converts the set into itself is then the Galois group of . ${\displaystyle f(x)=0}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle B}$ ${\displaystyle h(X_{1},\dotsc ,X_{n})}$ ${\displaystyle n}$ ${\displaystyle f(x)=0}$ ${\displaystyle h(x_{1},\dotsc ,x_{n})=0}$ ${\displaystyle X_{i}}$ ${\displaystyle B}$ ${\displaystyle f}$

In order to have to consider only polynomials in one variable for the sake of simplicity , Galois formed the resolvent named after him today:

${\displaystyle t=m_{1}x_{1}+\dotsb +m_{n}x_{n}}$

Whatever is possible, the whole numbers are to be chosen in such a way that the values ​​resulting from all permutations of the roots are different in pairs. Each root of the equation can then be expressed as a polynomial of the value (known in today's terminology as the theorem of the primitive element :) so that the set can be characterized on the basis of a polynomial equation for the value . ${\displaystyle m_{i}}$ ${\displaystyle \sigma }$ ${\displaystyle x_{i}}$ ${\displaystyle t_{\sigma }}$ ${\displaystyle x_{i}}$ ${\displaystyle f(x)=0}$ ${\displaystyle t}$ ${\displaystyle K(t)=K(x_{1},\dotsc ,x_{n})}$ ${\displaystyle B}$ ${\displaystyle t}$

literature

• Jörg Bewersdorff : Algebra for beginners: from equation resolution to Galois theory Springer Spectrum, 5th edition 2013, ISBN 978-3-658-02261-7 , doi : 10.1007 / 978-3-658-02262-4
• Ian Stewart : Galois Theory , Chapman and Hall 2004, ISBN 978-1584883937
• Jean-Pierre Tignol: Galois Theory of Algebraic Equations , World Scientific 2001, ISBN 978-9810245412 , doi : 10.1142 / 9789812384904
• Harold Edwards : Galois Theory , Springer Verlag 1984, ISBN 038790980X

Older literature on Galois theory with resolvents:

• James Pierpont Galois Theory of Algebraic Equations , I, Annals of Mathematics, Volume 1, 1899/1900, p. 113, AMS Colloquium Lectures 1896
• Leonard Dickson Introduction to the Algebraic Theory of Equations , Wiley 1903

Individual evidence

1. ^ Joseph-Louis Lagrange: Réflexions sur la résolution algébrique des equations. , Meeting reports of the Berlin Academy 1770/71
2. ↑ See e.g. B. Harold Edwards Galois Theory
3. ↑ Jean-Marie Arnaudiés, Annick Valibouze Lagrange Resolvents , Journal of Pure and Applied Algebra, Volume 117/118, 1997, pp. 23-40, pdf
4. ^ RWD Nickalls: The quartic equation: invariants and Euler's solution revealed. (PDF; 548 kB) In: The Mathematical Gazette. Vol. 93, 2009.
5. ↑ For example Helmut Knaust The quartic formula , or Ian Stewart Galois theory , Chapman and Hall 2004, p. 11
6. ↑ Also Carl Gustav Jacobi knew this (1831). Malfatti started from the formalism of the Lagrange resolvent. For Malfatti see Bewersdorff, Algebra für Einsteiger , p. 90
7. ↑ Representation here after Ian Stewart. The special cases in which it is solvable by radicals are analyzed by GN Watson in a lecture that was later published in Mathematical Intelligencer, Volume 24, 2002, No. 4
8. ↑ The alternating group of order 5 is a simple group, it is not possible to form a normal divisor chain with cyclic groups as factor groups up to identity. ${\displaystyle A_{5}}$
9. ↑ Bewersdorff Algebra for Beginners , p. 126