Laplace Plain

Illustration of the Laplace plane of a celestial body as a time-averaged orbit plane
Gray: Laplace plane
Blue: Current orbit plane
M (black): Central body
m (red): Circumferential body
L : Orbital angular momentum vector
Green: Nodal line

In celestial mechanics, the Laplace plane denotes the orbit plane of a body (e.g. a planet or satellite ), averaged over long periods , that moves in an orbit around a central object ( e.g. the sun or a planet).

The Laplace planes of most of the large moons in our solar system, especially those of the large gas planets , are based on the equatorial plane of the respective central planet . An exception is the Earth's moon , whose Laplace plane lies with great accuracy in the ecliptic . The Laplace planes of artificial satellites in the higher earth orbit and those of some (mainly smaller) moons of other planets lie between the orbital plane and the equatorial plane of their central body and must therefore be calculated explicitly.

In 1805, Pierre-Simon Laplace was the first to introduce this reference plane to describe the orbital properties of Saturn's moon Iapetus , the largest moon in the solar system, in which this plane deviates significantly from both the equatorial plane and the orbital plane of the planet.

introduction

If a body moves around a central object, a current orbit plane can be assigned to it at any point in time . This is the plane in which both the distance vector from the central object to the body and the velocity vector of the moving body lie. The orbital angular momentum vector of the body is perpendicular to this plane. If the movement of the body is not subject to any torque , the orbital angular momentum of the body does not change and the orbital plane of the body is correspondingly constant over time. This is the case, for example, when the central object is exactly spherically symmetrical and no external forces act on the system.

In reality, however, the central objects are neither exactly spherically symmetrical (the planets are more or less flattened), nor is the movement free from external forces (from the sun, other planets etc.). Therefore, torques act on the rotating bodies, which lead to a change in the orbital plane, which in most cases is small in the course of a few revolutions around the central object, but over time leads to a precession movement of the orbital angular momentum. In the case of the planetary, lunar and satellite orbits, this effect can be modeled over longer periods of time by the action of a constant torque on a rapidly moving top . The orbital plane then fluctuates with a certain time period around an orbital plane averaged over long times (Laplace plane). The angle of inclination of the current plane of the orbit against the Laplace plane remains approximately constant, only the position of the planes to one another changes.

Research history and the Saturn moon Iapetus

When analyzing the orbits of the great moons of the planet Jupiter, the French mathematician Laplace found that , like the orbits of the planets, they run in one plane over short periods of time (a few years). However, over medium periods of time - often a few years to decades - this orbital plane is variable: an effect that has been known for the earth's moon since ancient times, as it is closely related to the seasonal occurrence of solar and lunar eclipses . Laplace saw that the orbital plane of the moons performs a gyratory vortex movement over long periods of time. For the Earth's moon, this rotation of the so-called lunar nodes has been known for a long time, with the period of this rotation being 18.6 years. If, instead of the plane of the orbit, one looks at the pole of the plane of the orbit, i.e. the point on the celestial sphere at which an imaginary line that is perpendicular to the plane of the orbit (the normal ) pierces this sphere, this pole performs a circular motion on the celestial sphere. At the Earth's moon, this circle has a diameter of about 10 ° (twice the inclination of the moon's orbit ) and its center is the pole of the ecliptic (i.e. the plane of the earth's orbit). In the case of Jupiter's moons, however, the center of these circles is the “celestial pole of Jupiter”, ie the point at which the Jupiter axis pierces the celestial sphere. Laplace presented the corresponding theory, which attributes this nodal movement to the flattening of Jupiter and the torque exerted by it (and not the torque exerted by the sun, which is decisive for the Earth's moon).

Position of the Laplace planes of important Saturn moons in relation to the plane of rotation and orbit of Saturn. The poles of the different planes are projected onto the ecliptic in the diagram, so that the pole of the ecliptic is at the origin. The spring point lies in the direction of the x-axis. Also shown are the poles of the orbital planes of the outer planets.

In contrast to the other then known satellites of the gas planets, with the discovery of Iapetus in 1671, a Saturn moon was known early on, which orbits its central planet at a fairly large distance (about 3.5 million km). When analyzing the orbit of this moon, the French mathematician Laplace found that , like the orbit of all other moons and planets, it runs in one plane for short periods of time (a few years). Over medium periods of time - in this case several decades - the corresponding orbital plane is again variable, as was already observed by the Earth's moon and Jupiter's moons. Although Iapetus had only been observed for 134 years in 1805 and the observation data for Saturn's moons did not match the accuracy of the data for Jupiter's moons, Laplace saw that the moon's orbital plane moves in a gyro-like vortex over a period of several millennia. In Iapetus, the corresponding circle, which the pole of the plane describes, has a diameter of about 15 °. However, the pole of Saturn's orbit plane is not in its center, nor is the pole of Saturn's equatorial plane (i.e. the point where the axis of rotation of the planet cuts through the celestial sphere). Instead, as you can see in the diagram opposite, the center lies between the pole of Saturn's orbit plane and the pole of Saturn's equatorial plane. All other moons known at the time (these were the four Galilean moons , six other Saturn moons , as well as two Uranus moons ) have orbits that incline little more than one degree to the equatorial plane of the central planet. With measurements of high precision one finds that the orbital poles of these moons also perform circular movements, namely around the pole of the equatorial plane of the planet.

The center of the circle, on which the orbital pole of a moon moves, is the pole of the orbital plane averaged over long periods of time , which itself is invariable with time: the Laplace plane. In the near-planet moons of the massive and distant gas planets, this coincides with the equatorial plane. In the case of the Earth's moon, as with the outer Saturn moon Phoebe, discovered in 1888 (planetary distance about 13 million km), this coincides very precisely with the pole of the orbital plane of the respective planet. The fall of the moon Iapetus shows that there is a zone of intermediate distance from the planet in which the Laplace plane takes on an intermediate form. Today, in the 21st century, hundreds of planetary moons are known and artificial satellites have been launched in planetary orbits, the exact orbital dynamics of which generalize the special case of Iapetus. This fact calls for a clarification of the question of what the exact dynamics of the orbital planes looks like in the general case.

Celestial mechanical explanation

The ideal case of a small body moving around a spherical central object is described by Kepler's two-body problem or the single center problem . Since the gravitational field of the spherical central object is radially symmetrical, no torque acts on the rotating body and the orbital angular momentum of the body is constant over time in this case. This requires, on the one hand, the validity of Kepler's second law and, on the other hand, the fact that the movement of the small body takes place in a plane that does not change over time, the plane of the path .

A - celestial body
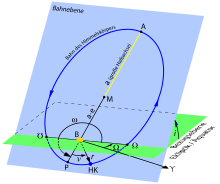
B - central object
green - reference plane (Laplace plane)
blue - orbital plane (orbital plane)
i - inclination
Ω - length of the ascending node

The orbits of real bodies in orbit around a central object, such as planets orbiting around the sun, moons orbiting their planets, or artificial satellites, can only be roughly treated as a two-body problem. Deviations from the spherical shape of the central object and the presence of other massive bodies outside the system lead to a disturbed two-body system . Such a disturbed system can still be described over short periods of time by the orbit elements of a Kepler ellipse, but the disturbances lead to a change in the orbit elements over time. In particular, a torque that acts on the revolving body leads to a temporal change in the orbit plane, which in celestial mechanics is generally indicated by the orbit inclination (inclination) i and the position angle (argument) of the ascending node Ω in relation to an unchangeable reference plane .

The nature of the torques T that occur is often such that they are quite small in relation to the angular momentum L or That is, the angular momentum changes very little during one revolution of the body around the central object, in the formulas:, where ω is the angular frequency of the body during revolution. In this case, the body can be viewed as a fast top with its axis of rotation pointing in the direction of the orbital angular momentum. As a result of the torque, the axis of rotation changes its direction in such a way that it wanders briefly around a central axis of rotation , which in turn wanders around a precession pole with long periods . The plane perpendicular to the direction of the precession pole can long-term be regarded as the mean orbit plane and is called the Laplace plane . ${\displaystyle T/L\ll \omega }$

Planets, moons and satellites often move on ellipses of relatively little eccentricity around their central body, and the torques that act on the body are mostly caused by the mechanisms described in the three following paragraphs.

Deviations of the central body from the spherical shape

As long as both bodies in a two-body system have an exactly spherically symmetrical structure, the gravitational field in the resulting equivalent single center problem is exactly radially symmetrical and there is no torque between the rotating bodies. However, deviations from the spherical shape lead to the occurrence of a torque and thus to a change in the plane of the path over time. In the celestial mechanical context, the dominant source of this torque is the quadrupole moment of the central body, which is largely due to the flattening along the axis of rotation of the body. The torque, which is averaged over a period of rotation, is perpendicular to the axis of rotation of the central body and perpendicular to the momentary angular momentum of the rotating body. As a result, the amount of angular momentum does not change, only the direction precesses around the axis of rotation of the central body. The conservation of angular momentum also has a reaction to the intrinsic angular momentum of the central body, which thereby precesses around the precession pole of the rotating body, but generally much more slowly. This effect of the earth's moon is, for example, one of the main reasons for the lunisolar precession of the earth's axis. ${\displaystyle J_{2}}$

If the axis of rotation of the central body is assigned a direction vector which, neglecting the reaction just described, can be regarded as constant over not too long periods of time, an exact calculation shows that the angular velocity of the orbital movement precesses around the axis of rotation . The scalar product does not change with time, i.e. This means that the orbit inclination i relative to the equatorial plane of the central object , which is thus the Laplace plane, does not change. The orbit node argument then travels at an angular velocity of ${\displaystyle {\vec {n}}}$ ${\displaystyle {\vec {\omega }}}$ ${\displaystyle {\vec {n}}}$ ${\displaystyle \langle {\vec {\omega }},{\vec {n}}\rangle =:\omega \cos i}$

${\displaystyle {\dot {\Omega }}=-{\frac {3J_{2}R^{2}\omega }{2a^{2}}}\cos i,}$

with the radius R of the central body and the semi-major axis a of the orbit.

For planets, which can generally be assumed to be ellipsoids of revolution, the quadrupole moment can be calculated from the moment of inertia I and the flattening f . For example, for the earth f ≈ 1/298 and I ≈ 0.33 MR ² thus J ₂ ≈ 0.0011 in good agreement with the more precise value J ₂ = 0.001082. ${\displaystyle J_{2}=I\cdot f/(MR^{2})}$

If you put this into the formula above and calculate the period of the nodal rotation for a satellite in near-earth, almost equatorial orbit, you get a nodal migration of about 10 ° per day against the orbital direction of the satellite, i.e. that is, the knot circles the earth's equator once in about 36 days.

For Jupiter one finds J ₂ ≈ 0.0147 and a radius of R ≈ 71,500 km. The moon Io orbits the planet at a distance of about a ≈ 421,000 km and the orbit node moves accordingly by about 47 ° per year and needs about 7.66 years for a full revolution, in good agreement with the measured 7.42 years. The already low orbit inclination of 0.05 ° compared to Jupiter's equatorial plane remains constant in good agreement with the model presented here, a fact that neither applies to artificial satellites in Earth orbit nor to the Earth's moon.

For the Earth's moon, the inclination with respect to the Earth's equator varies between 18 ° and 28.5 ° with a period of 18.6 years. The flattening of the earth would only cause a rotation of the nodes of about 2.1 ° per millennium with a constant inclination, so that the dynamics of the lunar nodes must have another cause; it is now presented.

External disturbances using the example of the earth's moon

Illustration of the migration of the orbit node of an orbit disturbed by an external body. It denotes: E: central object (e.g. earth) M: revolving body (e.g. moon) O: orbit of M (the part above the Laplace plane is thicker) R: direction of the vectorial angular velocity P: precession cone from RS: disruptive body (e.g. sun) B: relative orbit of S (e.g. ecliptic) L: Laplace plane (e.g. ecliptic planes)

If a two-body system is placed in an environment in which other objects interact with the two bodies, then, under certain conditions, the movement of the two bodies can be treated in terms of perturbation theory . With this approach, it is assumed that the two-body system can continue to be described for a short time in the form known from the undisturbed problem. However, constant orbit parameters will actually develop dynamically over medium and long periods of time. In this section a certain special case of the disturbance of a Kepler ellipse shall be described, whereby the interest again lies in the orbital elements inclination i and argument of the ascending node Ω. For this purpose, one proceeds from the assumptions that the revolving body can again be described as a fast top and that the interfering bodies move quickly in relation to the rate of change of the orbital elements. As an example of such a model, the earth's moon is chosen, which moves around the earth at about 13 times the angular speed with which the main disruptive body, namely the sun , moves relative to the earth-moon system. The change in the relevant path element Ω takes place at an angular velocity that is again about 18 times lower.

In such cases, an acceptable result is obtained if such a system is viewed as a fast gyroscope on which a force acts based on a mass distribution resulting from a time averaging of the disturbance masses over their orbits relative to the two-body system. Is this a single dominant interfering body which moves relative to the system at a constant pitch and constant speed, one can thus a one-dimensional ground ring with appropriate mass M and radius R out. The torque that this mass ring causes on the rotating body creates a change in the direction of the angular momentum and thus the plane of the path.

The ascending node of the orbit therefore moves at an angular velocity of

${\displaystyle {\dot {\Omega }}=-{\frac {3GM}{4r^{3}\omega }}\cos i,}$

where M is the mass of the bluff and r is its distance from the system. i now denotes the orbital inclination ( ) in relation to the orbital plane of the disruptive body , which is the Laplace plane here and whose normal is perpendicular to it. As in the previous section, it also applies here that the amount of the angular velocity and the inclination of the path are constant over time. ${\displaystyle \cos i=\langle {\vec {\omega }},{\vec {n}}\rangle /\omega }$ ${\displaystyle {\vec {n}}}$

If the disruptive body, as in the case of the earth-moon system, is the central body of a larger overall system (e.g. solar system ), the mass and the distance of this body can be eliminated in the above formula using Kepler's third law and you get

${\displaystyle {\dot {\Omega }}=-{\frac {3\omega _{0}^{2}}{4\omega }}\cos i,}$

where ω ₀ is the angular velocity of the disruptive body (sun). In the case of the Earth's moon, one can now read directly that (neglecting the orbit inclination) the lunar nodes move at an angular velocity that is about 4/3 ω / ω ₀ ≈ 1.33 · 13.4 ≈ 17.8 times slower is than the relative angular velocity of the sun - in other words: the knots rotate a full 360 ° every 17.8 years. The observed value of 18.6 years only results from a more precise calculation of the lunar orbit. The orbital inclination of the moon during this hike of the knot, apart from short-period fluctuations, is constant about 5 ° in relation to the ecliptic (Laplace plain). However, if one uses the data of Jupiter's moon Io, for example, one gets that the nodes would take almost 40,000 years for a full orbit - an effect that is almost four powers of ten smaller than that caused by the flattening of the central planet.

Combination of both cases

In many celestial mechanically relevant cases, the two effects just described are of comparable magnitude. If in such a case the axis of rotation of the central body and the orbital angular momentum of the outer disruptive body are parallel , both effects add up and one obtains:

${\displaystyle {\dot {\Omega }}=-\left({\frac {3GM}{4r^{3}\omega }}+{\frac {3J_{2}R^{2}\omega }{2a^{2}}}\right)\cos i.}$

The precession takes place circularly around the common direction of the axis of rotation of the central body and the orbital angular momentum of the disruptive body. The same applies to the superposition of several external disturbances, which all occur in the same plane. While this assumption is often justified for external disturbances - the sun and moon disturb satellites in Earth orbit both around the ecliptic, the small outer moons of Jupiter are disturbed by the sun and Saturn also around the ecliptic, etc. - the planets' equatorial planes often deviate significantly from the Ecliptic plane. For example, the Earth's equator is 23.5 °, the Saturn's equator 26.8 ° inclined to the ecliptic and in Uranus the planes are almost perpendicular to each other. As a result, both artificial satellites in earth orbit and the large Saturn moon Iapetus, for which both effects are of comparable magnitude, cannot be described by the above equation. Instead, the overlay i. General to a complex dynamic with a precession and a pole that lies between the axis of rotation of the central body and the angular momentum of the disruptive body. This also means that the orbit inclination is not constant with respect to the Laplace plane , but fluctuates periodically between a minimum and a maximum value. How strong this fluctuation in the path inclination is depends, in addition to the magnitudes of the two torques, also essentially on the angle between these two. This effect is therefore particularly serious for the planet Uranus, whose equatorial plane is almost perpendicular to its orbit.

Examples

Jupiter moons

Position of the Laplace planes of important Jupiter moons in relation to the plane of rotation and orbit of Jupiter. The poles of the different planes are projected onto the ecliptic in the diagram, so that the pole of the ecliptic is at the origin. The spring point lies in the direction of the x-axis. Also shown are the poles of the orbital planes of the outer planets.

In the system of the numerous moons of Jupiter, the various effects described above can be exemplified. As you can see in the graphic opposite, the poles of the Laplace planes of the inner moons are all arranged near the axis of rotation of the central planet at the bottom left of the diagram. The Laplace Plain of Callisto (IV), which is 1.9 million km away from Jupiter, is already clearly drawn in the direction of the plane of the orbit of Jupiter and thus the plane in which the sun acts as a disruptive body .

The nearest outer moon Themisto (XVIII), which is about 7.5 million km away from Jupiter, has a Laplace plane, which is mainly influenced by the orbital plane and hardly by the equatorial plane (top right in the diagram). All other outer moons of Jupiter are arranged in this area. However, it becomes immediately clear that the interplay between the equatorial and orbital planes of Jupiter alone is not sufficient to explain the Laplace planes of these moons. Rather, these lie in a large cloud around the plane of the orbit of Jupiter. The reason for this are the torques that act in the direction of the orbital poles of the three larger planets Saturn, Uranus and Neptune, which are therefore also shown. This effect can be clearly seen in the first diagram of this article for the Saturn moon Iapetus, whose Laplace plane is clearly drawn from the connecting line between the axis of rotation and the orbital pole in the direction of the orbital poles of the planets further out.

A particularly extreme case is the Laplace plane of Ananke (XII), which is inclined almost three degrees above the orbit plane of Jupiter and also lies beyond the orbit plane of Saturn in the diagram. Ananke is a blatant outlier among all known moons of Jupiter, which can only be explained by the orbital disturbances that occur specifically here.

Remarks

1. ↑ The direction of the vectorial angular velocity is parallel to the orbital angular momentum.
2. ↑ Assuming a path with little eccentricity, a more precise calculation leads to a change in the vectorial mean angular velocity of the orbiting body of

   ${\displaystyle {\dot {\vec {\omega }}}=-{\frac {3J_{2}R^{2}}{2a^{2}}}\langle {\vec {\omega }},{\vec {n}}\rangle {\vec {n}}\times {\vec {\omega }},}$

   where the dimensionless quadrupole moment, the direction vector of the axis of rotation of the central object, R denotes its radius and a denotes the major semi-axis of the orbit (the angle brackets represent the scalar product ). Due to the vector product , the change in the angular velocity is perpendicular to the angular velocity, so that it does not change its amount over time. ${\displaystyle J_{2}}$ ${\displaystyle {\vec {n}}}$
3. ↑ The quadrupole moment of a homogeneous ellipsoid of revolution is where f is the flattening of the body. Real planets, however, are not homogeneous; their density decreases with increasing distance from the center. Assuming that the body is made up of layers of equal density, the quadrupole moment is given by, where I denotes the moment of inertia. ${\displaystyle J_{2}={\frac {2}{5}}f,}$ ${\displaystyle J_{2}={\frac {I}{MR^{2}}}f}$
4. ↑ The torque that this mass ring causes on the rotating body generates a change in the vectorial mean angular velocity of the rotating body of:

   ${\displaystyle {\dot {\vec {\omega }}}=-{\frac {3GM}{4r^{3}\omega ^{2}}}\langle {\vec {\omega }},{\vec {n}}\rangle {\vec {n}}\times {\vec {\omega }},}$

   where M is the mass of the bluff, the direction vector of the angular velocity of the bluff and r is its distance from the system. ${\displaystyle {\vec {n}}}$
5. ↑ The corresponding differential equation for the angular velocity is

   ${\displaystyle {\dot {\vec {\omega }}}=-(A+B)\langle {\vec {\omega }},{\vec {n}}\rangle {\vec {n}}\times {\vec {\omega }}}$

   with and . ${\displaystyle A:=3J_{2}R^{2}/(2a^{2})}$ ${\displaystyle B:=3GM/(4r^{3}\omega ^{2})}$
6. ↑ The differential equation takes the form

   ${\displaystyle {\dot {\vec {\omega }}}=-\left(A\langle {\vec {\omega }},{\vec {n}}_{z}\rangle {\vec {n}}_{z}+B\langle {\vec {\omega }},{\vec {n}}_{s}\rangle {\vec {n}}_{s}\right)\times {\vec {\omega }}}$

   on. here denotes the direction vector of the axis of rotation of the central object, the direction vector of the angular velocity of the disruptive body. One can see from this differential equation that the amount of the angular velocity remains constant, since the change in the angular velocity is always perpendicular to the angular velocity itself (again due to the cross product in the differential equation). As a result, the size remains constant. However, the angle of the path plane is now constant neither to the axis of rotation of the central body nor to the direction of the angular velocity of the disruptive body . The angular velocity instead wanders around a precession pole that lies between and . The precession around this pole is no longer circular, but elliptical (more precisely, the curve is an ellipse projected onto a sphere). ${\displaystyle {\vec {n}}_{z}}$ ${\displaystyle {\vec {n}}_{s}}$ ${\displaystyle {\dot {\vec {\omega }}}}$ ${\displaystyle B}$ ${\displaystyle {\vec {n}}_{z}}$ ${\displaystyle {\vec {n}}_{s}}$ ${\displaystyle {\vec {n}}_{z}}$ ${\displaystyle {\vec {n}}_{s}}$
7. ↑ If one takes a closer look at the above DGL, one sees that the equation, since A and B are constant, is quadratic in . You can use the DGL as a ${\displaystyle {\vec {\omega }}}$

   ${\displaystyle {\dot {\vec {\omega }}}={\vec {\omega }}\times (M{\vec {\omega }})}$

   write, taking the matrix

   ${\displaystyle M:=A|{\vec {n}}_{z}\rangle \langle {\vec {n}}_{z}|+B|{\vec {n}}_{s}\rangle \langle {\vec {n}}_{s}|}$( Bra-Ket notation),

   Rank 2 has. The two eigenvectors of the matrix are linear combinations of the direction vectors and . One eigenvector indicates the direction of the normal to the Laplace plane, the other the direction of the major semi-axis of the elliptical curve that describes the vectorial angular velocity around this pole. ${\displaystyle {\vec {n}}_{z}}$ ${\displaystyle {\vec {n}}_{s}}$
8. ↑ If one neglects this effect, one comes to an approximation of the above differential equation for small angles between the planes:

   ${\displaystyle {\dot {\vec {\omega }}}=-(A+B)\langle {\vec {\omega }},{\vec {n}}_{L}\rangle {\vec {n}}_{L}\times {\vec {\omega }},}$

   where the normal is on the Laplace plane , which is precisely the weighted mean of the normals on the equatorial and interference plane. ${\displaystyle {\vec {n}}_{L}:=(A{\vec {n}}_{z}+B{\vec {n}}_{S})/(A+B)}$

Individual evidence

1. ^ ^{A b} Pierre-Simon Laplace : Mécanique céleste . (English translation). tape 4 . Little & Brown, Boston 1829, chap. 17 , p. 315 ff . (English, archive.org - French: Traité de Mécanique céleste . 1805. Translated by Nathaniel Bowditch).
2. ^ RR Allan, GE Cook: The Long-Period Motion of the Plane of a Distant Circular Orbit , Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 280, No. 1380 (Jul. 7, 1964), pp. 97-109
3. ^ S. Laplace, chap. IV, p. 62ff.
4. ↑ ^{a b} satellite railways project TU-Munich ( memento of the original from September 30, 2007 in the Internet Archive ) Info: The archive link was automatically inserted and not yet checked. Please check the original and archive link according to the instructions and then remove this notice. 
5. ↑ NASA Earth Fact Sheet
6. ↑ NASA Jupiter Fact Sheet ( Memento of the original from October 5, 2011 on WebCite ) Info: The archive link was automatically inserted and not yet checked. Please check the original and archive link according to the instructions and then remove this notice. 
7. ↑ ^{a b} Planetary Satellite Mean Orbital Parameters from JPL
8. ↑ ^{a b} M. Schneider: Himmelsmechanik , chap. 26, Vol. 2, BI Wiss. Verlag, Mannheim (1993), pp. 542-550