productivity

This article applies to productivity as an economic metric. For productivity in linguistics, see word formation # classification options .

Productivity is an economic indicator that describes the relationship between the goods / services produced and the production factors required for them .

General

The economic subjects ( private households , companies and the state with its subdivisions such as public administration , state-owned companies , municipal companies ) are required to deal rationally with scarce resources ( rational principle ). This also includes productivity as the sum of productive measures taken by economic entities and their behavioral patterns , usually related to a system or a production process with production factors and products . Measured against the rational principle, everything can be classified as productive if the resources used are in a favorable relationship to the effect achieved. Conceptually, productivity is closely related to constructiveness and the opposite of destructiveness .

Economic Definitions

In economics and business administration , productivity is understood to be an economic or business indicator that reflects the (quantitative) relationship between what is produced ( English output ) and the means used for this in the production process (production factors, English input ).

In order to meet these requirements, a given output ( minimum principle ) can either be achieved with the lowest possible input or the largest possible output ( maximum principle ) with a given input . This means that productivity is also a specific expression of the rational principle. Maintaining productivity as a behavioral maxim also enables the goal of maximizing profit or maximizing utility to be achieved . There is thus target harmony between these goals .

Difference between productivity and profitability

While productivity deals with the comparison of output and input, profitability relates costs / effort to income / revenue . The economics are therefore value-based sizes based on productivity, however quantitative .

detection

The overall productivity in companies is determined using the following formula:

${\displaystyle {\text{Produktivität}}={\frac {\text{Ausbringungsmenge}}{\text{Einsatzmenge}}}={\frac {\text{Output}}{\text{Input}}}}$

The output is specified as a quantity per unit of time , i.e. viewed as a flow quantity . The input can also be a flow variable, for example the number of working hours in a year ( working time ) or depreciation in a year. It can also be a stock variable, for example the average number of people in employment in a year or the average capital stock in a year.

Since the goods / services produced are of very different types and the composition of production according to different goods can also change over time , it is necessary to value the different goods with prices in order to be able to specify the total output as a one-dimensional quantity. For this purpose, the goods are valued at market prices , if such exist . Goods for which there are no market prices are valued at production cost . Furthermore, pure price changes are deducted from the output with the help of price adjustment procedures. One method is to calculate in constant prices for a base year.

The same valuation problem also arises with the production factor capital , since the capital stock is composed of various goods. For the production factor labor, on the other hand, physical quantities such as the number of persons in employment or the number of hours worked are used.

Productivity can be broken down according to the different production factors:

• ${\displaystyle {\text{Arbeitsproduktivität}}={\frac {\text{Ausbringungsmenge}}{\text{Eingesetzte Arbeitsstunden}}}}$

• ${\displaystyle {\text{Maschinenproduktivität}}={\frac {\text{Ausbringungsmenge}}{\text{Eingesetzte Maschinenstunden}}}}$

• ${\displaystyle {\text{Materialproduktivität}}={\frac {\text{Ausbringungsmenge}}{\text{Materialeinsatzmenge}}}}$

Factor productivity

When determining the factor productivity, the amount of goods produced is set in relation to the input amount of a factor.

These statistically measured productivities cannot be understood causally in the sense that, for example, rising labor productivity shows that workers are becoming “more diligent” and that falling capital productivity shows that capital is producing less and less. Rather, increasing labor productivity is the result of the fact that more and more “ capital ”, actually means of production , is used per worker . Typically, therefore, labor productivity increases in the long term, while “capital” productivity stagnates or even declines.

In neoclassical theory , the assumption applies that the factors of production are rewarded according to their productivity - which does not mean that this also happens in practice. The reasons for this can be found in market errors and externalities. With the help of the statistically measured productivities it can be checked whether this is the case.

Labor productivity

The best known and most widely used factor productivity is labor productivity . This is mainly due to the fact that the amount of work used is easier to determine than, for example, the wear and tear or the stock of the capital employed, i.e. machines, buildings and (when considering overall economic productivity) infrastructure facilities.

The economic formula for labor productivity per hour worked is:

${\displaystyle {\text{Arbeitsproduktivität }}Pi={\frac {BIP_{\mathrm {real} }}{\text{Arbeitsvolumen}}}={\frac {BIP_{\mathrm {real} }}{Et\cdot h}}}$

where the real gross domestic product , the number of employed persons and the number of hours worked per employed person (see development of labor productivity ). ${\displaystyle BIP_{\mathrm {real} }}$ ${\displaystyle Et}$ ${\displaystyle h}$

The economic formula for labor productivity per employed person is:

${\displaystyle {\text{Arbeitsproduktivität }}Pi={\frac {BIP_{\mathrm {real} }}{Et}}}$

or

${\displaystyle {\text{Arbeitsproduktivität }}={\frac {\text{Ergebnis}}{\text{Arbeitsaufwand}}}}$

The economic hourly output results from the comparison of sales volume and hours worked:

${\displaystyle {\text{Stundenleistung}}={\frac {\text{Absatzvolumen}}{\text{Arbeitsstunden}}}}$.

If the sales volume increases with constant working hours, the productive hourly output has improved and vice versa.

Capital productivity

The Federal Statistical Office shows capital productivity by comparing the gross domestic product at constant prices (most recently in 1995) to the capital stock . The latter is the gross fixed assets also calculated in constant prices.

The addition of different types of capital to a total capital stock is based on dubious assumptions that have been criticized in the course of the capital controversy .

Empirical Findings

OECD economic data presented graphically

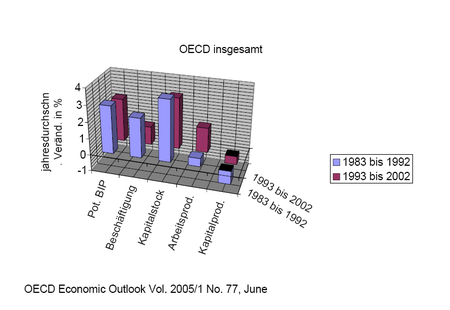
According to OECD , Economic Outlook No. 77, June 2005 the following results:

In the OECD countries, i.e. in the industrialized countries, the potential production (production with normal utilization of the capital stock) increased by an annual average of 2.9% from 1983 to 1992. This slowed somewhat to an annual average of 2.6% from 1993 to 2002.

Employment grew an annual average of 2.4% and 1.1% in these specified periods. So employment growth has slowed in the OECD.

For labor productivity, this results in a growth of approximately 0.5% in the first and 1.5% in the second period. Labor productivity growth has therefore accelerated.

The capital stock grew by 3.7% or by 3.1% on an annual average, i.e. faster than production. Capital productivity has accordingly decreased, an annual average of 0.8% from 1983 to 1993 and by 0.5% from 1993 to 2002.

As a rule, labor productivity increases in the medium and long term, while capital productivity tends to decrease, as is the case here in the OECD countries. A notable exception is the USA, for which the OECD reports an annual average growth in capital productivity of 0.1% from 1983 to 1992 and of 0.1% from 1993 to 2002 as well.

A long-term decline in capital productivity is problematic, as this means that in the long term the overall economic return on capital (capital income in relation to the capital stock) can only be maintained if the share of labor income in GDP is reduced, although this would of course end at the latest when this wage share would have reached zero.

Marginal productivity

→ Main article : marginal product

In addition to the previously considered average productivity of the factors, their marginal productivity is also of economic and economic interest:

${\displaystyle {\frac {\partial x}{\partial r_{i}}}}$

This indicates how much the output increases if the factor input increases by one unit, assuming the other factors remain constant. The marginal productivity of the labor factor can e.g. B. measured by the amount by which output increases when an additional hour is worked. Marginal productivities are of particular interest because, according to theory, they determine the market price for the factor in perfect factor markets . In general, after the value of marginal productivity : . And in the optimum, the WGP corresponds to the factor price (to determine the optimal factor input quantity). ${\displaystyle {\text{WGP}}={\text{Grenzproduktivität}}\cdot {\text{Outputpreis}}}$

In most cases one assumes a positive but decreasing marginal productivity, i.e. H. if the input is increased, the output will increase. However, the amount of the increase decreases with the increasing starting level of the input (see Income Act ).

Mathematically, the marginal productivity of a factor can be determined as a partial derivative of the production function according to this factor.

Total factor productivity

Empirically it can be observed that the growth in output Y can not only be explained by the growth of inputs labor A and capital K, but that an inexplicable remainder remains, so to speak. That part of the growth rate of Y that cannot be explained by changes in the amounts of A or K input is called the total factor productivity . It can be interpreted as a measure of technical progress that ensures a growth in output Y regardless of the use of production factors.

Empirical Findings

In a study, the importance of different location factors for the total factor productivity of a region was examined using data from 257 regions of the EU. For the analysis, potentially influencing properties of the regions were taken into account, such as B. the degree of specialization in the field of manufacturing , settlement structure , population density and the economic development level of the region. Had the strongest positive influence on the total factor productivity of a region (in descending order):

1. the proportion of employed people with a degree in creative professions (e.g. natural and social sciences , life science and health , teachers, engineering ...),
2. the number of registered patents per thousand inhabitants (as a measure of technological capital) and
3. the cultural diversity .

The degree of specialization in manufacturing and the annual average temperature had a negative impact .

Development of labor productivity

Above is the equation of labor productivity:

${\displaystyle Pi={\frac {BIP_{\mathrm {real} }}{\text{Arbeitsvolumen}}}}$

The absolute numbers of labor productivity are often less informative than the development of labor productivity in relation to a base year. To do this, the above equation is divided by a base year for any year:

${\displaystyle Pi_{\mathrm {rel} }={\frac {Pi}{Pi_{\text{Basis}}}}={\frac {\frac {BIP}{\text{Arbeitsvolumen}}}{\frac {BIP_{\text{Basis}}}{{\text{Arbeitsvolumen}}_{\text{Basis}}}}}={\frac {\frac {BIP}{BIP_{\text{Basis}}}}{\frac {\text{Arbeitsvolumen}}{{\text{Arbeitsvolumen}}_{\text{Basis}}}}}={\frac {BIP_{\mathrm {rel} }}{AV_{\mathrm {rel} }}}}$

The data used are published by the German Federal Statistical Office and can be found in the WP under the keywords GDP and volume of work (abbreviated AV). The annual increase in labor productivity ( ) is also given. ${\displaystyle \Delta Pi}$

relative labor productivity in Germany on the base year 1995

year	${\displaystyle BIP_{\mathrm {rel} }}$	${\displaystyle BIP_{\mathrm {rel} }}$	AV	${\displaystyle AV_{\mathrm {rel} }}$	${\displaystyle Pi_{\mathrm {rel} }}$	${\displaystyle \Delta Pi}$
	Base	Base	Million h	Base	Base	%
	1960	1995		1995	1995
1950
1951	0.49	0.16
1952	0.53	0.18
1953	0.59	0.20
1954	0.64	0.21
1955	0.69	0.23
1956	0.77	0.26
1957	0.83	0.28
1958	0.88	0.30
1959	0.92	0.31
1960	1.00	0.34		1.22	0.28
1961	1.04	0.35	56470	1.22	0.29	3.83
1962	1.09	0.37	55690	1.20	0.30	6.27
1963	1.12	0.38	55020	1.19	0.32	4.00
1964	1.2	0.41	55371	1.20	0.34	6.46
1965	1.26	0.43	55329	1.20	0.36	5.07
1966	1.3	0.44	54483	1.18	0.37	4.77
1967	1.29	0.44	51764	1.12	0.39	4.44
1968	1.36	0.46	51507	1.11	0.41	5.95
1969	1.46	0.50	51812	1.12	0.44	6.72
1970	1.58	0.54	52075	1.13	0.47	7.67
1971	1.63	0.56	51428	1.11	0.50	4.46
1972	1.7	0.58	51029	1.10	0.52	5.10
1973	1.78	0.61	50800	1.10	0.55	5.17
1974	1.79	0.61	49402	1.07	0.57	3.40
1975	1.77	0.60	47122	1.02	0.59	3.66
1976	1.86	0.63	47271	1.02	0.62	4.75
1977	1.91	0.65	46959	1.02	0.64	3.37
1978	1.97	0.67	46837	1.01	0.66	3.41
1979	2.05	0.70	47368	1.02	0.68	2.89
1980	2.08	0.71	47611	1.03	0.69	0.94
1981	2.08	0.71	47047	1.02	0.69	1.19
1982	2.07	0.71	46268	1.00	0.70	1.19
1983	2.1	0.72	45572	0.99	0.72	2.99
1984	2.16	0.74	45642	0.99	0.74	2.69
1985	2.2	0.75	45663	0.99	0.76	1.80
1986	2.26	0.77	46003	0.99	0.77	1.96
1987	2.29	0.78	45988	0.99	0.78	1.36
1988	2.38	0.81	46474	1.00	0.80	2.84
1989	2.47	0.84	46645	1.01	0.83	3.40
1990	2.61	0.89	47412	1.03	0.87	3.95
1991	2.75	0.94	47990	1.04	0.90	4.09
1992	2.81	0.96	48140	1.04	0.92	1.86
1993	2.78	0.95	46773	1.01	0.94	1.82
1994	2.86	0.98	46438	1.00	0.97	3.61
1995	2.91	1.00	46025	1.00	1.00	2.66
1996	2.94	1.01	45455	0.98	1.02	2.29
1997	2.99	1.02	45365	0.98	1.04	1.90
1998	3.06	1.05	45744	0.99	1.05	1.49
1999	3.12	1.07	46096	1.00	1.07	1.18
2000	3.22	1.10	46691	1.01	1.09	1.88
2001	3.26	1.12	46715	1.01	1.10	1.19
2002	3.26	1.12	46225	1.00	1.11	1.06
2003	3.25	1.11	45909	0.99	1.11	0.37
2004	3.29	1.13	46129	1.00	1.12	0.74
2005	3.32	1.14
Annotation:

See also

• Bio , area , resource productivity
• Marginal product of labor
• Productivity paradox

Web links

Wikiquote: Productivity  - Quotes

• Andreas Dikow: Market-oriented concept for productivity management in manufacturing companies . (PDF; 1.12 MB)
• Measurement of labor input and labor productivity in Switzerland (PDF) Methods report by the Swiss Federal Statistical Office , July 2007
• Prosperity through productivity - Germany in an international comparison (PDF; 331 kB) - Expertise and documentation on economic and social policy. Friedrich Ebert Foundation , March 2009

Individual evidence

1. ↑ Helmut Weber, Profitability, Productivity and Liquidity: Quantities for Assessment and Control of Companies , 1998, p. 87
2. ↑ Hans Corsten, Production Management, 6th edition, 1996, p. 46 f.
3. ↑ REFA - Methodology of Working Studies , Part 1 “Basics”. Carl Hanser, Munich 1971, ISBN 3-446-14234-7 , p. 43 ff.
4. ↑ Helmut Weber, Profitability, Productivity and Liquidity: Sizes for Assessment and Control of Enterprises , 1998, p. 89 f.
5. ^ Emanuela Marrocu, Raffaele Paci: Education or Creativity: What Matters Most for Economic Performance? In: Economic Geography . tape 88 , no. 4 , October 2012, p. 369-401 , doi : 10.1111 / j.1944-8287.2012.01161.x ( wiley.com [accessed June 19, 2019]).