Shear law

In materials science , a shear law specifies how a material behaves under the influence of shear forces .

Shear laws are in technical fields such as engineering and construction used to estimate the maximum load of a structure. In geotechnical engineering , they are used to determine the maximum load-bearing capacity of the soil and to predict settlement .

Shear law by Charles Augustin de Coulomb

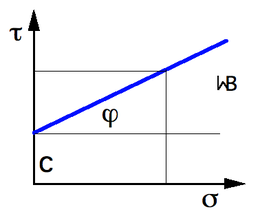
Coulomb's law of shear. With shear stresses above the blue line, permanent deformations occur.

In the shearing of a body contact stresses both in the direction of shear and perpendicular thereto. A tension perpendicular to the shear has an inhibiting effect on the shear. The greater it is, the greater the shear stress can become before permanent deformation occurs. This is similar to friction , which is able to keep a body from moving on an inclined plane . ${\ displaystyle \ tau}$

In addition, a holding force can act between grains or molecules of the body, which must be overcome before a part of the body shears off. The tension created by these forces is called cohesion .

The stress above which permanent deformation occurs is called the shear strength . It can be determined for all soils and rocks as well as for other natural substances (bulk and storage materials with a solid consistency) and for metals using Coulomb's law of shear : ${\ displaystyle \ tau _ {\ text {scher}}}$

{\ displaystyle \ tau _ {scher} = \ sigma \ cdot \ tan \ varphi + c}

With

the normal stress acting perpendicular to the shear , which is proportional to the pressure at the point in the body under consideration ${\ displaystyle \ sigma}$

the shear parameters
depending on the material
- Cohesion c
- internal friction angle φ .

Mohr-Coulomb breakage criterion

The Mohr-Coulomb rupture criterion states that a rupture of the solid (soil, rock, etc.) occurs when the shear stresses from the external load become greater than the shear strength, which is defined by the above. Equation of the “fracture line” or Coulomb shear line. The straight line can be shown in Mohr's diagram ;

there the break criterion means that

the Mohr's circle of tension of each soil particle must lie below the fracture line so that no fracture occurs: ${\ displaystyle \ tau <\ tau _ {fraction}}$
if he touches it, the limit state has just been reached.
There can be no circles of tension that lie above the shear line, because the ground would give way. Instead, the soil sample will shear (e.g., in a testing device such as a triaxial device ) along a fracture surface, i.e. H. she breaks for . ${\ displaystyle \ tau> \ tau _ {fraction}}$

Compressive strength

The compressive strength of a material as a function of the shear parameters c and φ can also be derived from Mohr's stress cycle . Mohr's circle is drawn for the fracture state of the material. According to the Mohr-Coulomb fracture criterion, the tangent to the circle ( fracture line) at the angle φ to the horizontal and its point of intersection with the vertical coordinate axis with the distance c from the zero point describe the fracture state. The greatest compressive stress that can be absorbed is then the intersection of the circle on the right with the horizontal coordinate axis. ${\ displaystyle \ sigma _ {d}}$

Expressed in formulas, the following applies for the biaxial compressive strength:

{\ displaystyle \ sigma _ {\ mathrm {d}} = {\ frac {1+ \ sin \ varphi} {1- \ sin \ varphi}} \ cdot \ sigma _ {3} + c \ cdot {\ frac { 2 \ cdot \ cos \ varphi} {1- \ sin \ varphi}}}

and for the special case (uniaxial compressive strength): ${\ displaystyle \ sigma _ {3} = 0}$

{\ displaystyle \ sigma _ {\ mathrm {d}} = c \ cdot {\ frac {2 \ cdot \ cos \ varphi} {1- \ sin \ varphi}}}

Use on soils with pore water

Pore water is a special feature of granular media such as soil .

If you press on a dry floor, the pores are mainly compressed. The individual grains move closer together and take over the pressure . If the pores are now filled with water, the situation is a little more complicated. The water is incompressible and first absorbs the external load as pore water pressure. Since there is a lower pore pressure at the side of the load , the water flows off at the lower pressure, the pores can deform (decrease), and the load can be transferred to the grains of the soil. This process is called consolidation of the soil. The pore water pressure that results from the load is called excess pore water pressure . This is reduced during consolidation.

If the soil is saturated with water, the weight forces are transferred from grain to grain. This transfer takes place according to Coulomb's law of matter. If a water-saturated soil is now loaded by an additional load, this creates an excess pore water pressure. For the time being, the grain structure does not feel any of this additional load, as the water absorbs the pressure. The grain-to-grain tension is initially the same as without additional loading.

Only over time, when the pore water runs off, will the grain-to-grain stresses increase until the additional stress is fully absorbed by the grain-to-grain stress. This must also be taken into account in the shear law. The Coulomb shear law only applies to grain-to-grain stresses. To calculate the grain-to-grain tension , the excess pore water pressure must be subtracted from the total tension : ${\ displaystyle \ sigma '}$ ${\ displaystyle u}$ ${\ displaystyle \ sigma}$

{\ displaystyle \ sigma '= \ sigma -u}

this leads to the expanded material law of Coulomb:

{\ displaystyle {\ begin {aligned} & \ tau = c + \ sigma '\ cdot \ tan \ varphi \\\ Leftrightarrow & \ tau = c + (\ sigma -u) \ cdot \ tan \ varphi \ end {aligned}} }

.

literature

Bernhard Wietek : Basic construction - introduction to theory and practice. 4th edition; Manz-Verlag, Vienna 2004, ISBN 978-3706812061
Bernhard Wietek: Steel fiber concrete. 2nd Edition; Vieweg + Teubner Verlag 2010, ISBN 978-3834805928
Achim Hettler , Karl-Eugen Kurrer : Earth pressure . Ernst & Sohn, Berlin 2019, p. 66ff, ISBN 978-3-433-03274-9